Ce este ciclul hamiltonian?
Ciclul sau circuitul Hamiltonian într-un grafic G este un ciclu care vizitează fiecare vârf al G exact o dată și revine la vârful de pornire.
- Dacă graficul conține un ciclu hamiltonian, acesta se numește Graficul hamiltonian altfel este non-hamiltonian .
- Găsirea unui ciclu hamiltonian într-un grafic este un lucru binecunoscut Problemă NP-completă , ceea ce înseamnă că nu există un algoritm eficient cunoscut care să îl rezolve pentru toate tipurile de grafice. Cu toate acestea, poate fi rezolvată pentru tipuri mici sau specifice de grafice.
Problema ciclului hamiltonian are aplicații practice în diverse domenii, cum ar fi logistică, proiectare de rețele și informatică .
Ce este calea hamiltoniană?
Calea Hamiltoniană într-un grafic G este o cale care vizitează fiecare vârf al lui G exact o dată și Calea Hamiltoniană nu trebuie să se întoarcă la vârful de pornire. Este o cale deschisă.
- Similar cu Ciclul Hamiltonian problemă, găsirea unui Calea Hamiltoniană într-un grafic general este de asemenea NP-complet și poate fi o provocare. Cu toate acestea, este adesea o problemă mai ușoară decât găsirea unui ciclu Hamiltonian.
- Căile Hamiltoniene au aplicații în diverse domenii, cum ar fi găsirea rutelor optime în rețelele de transport, proiectarea circuitelor și cercetarea teoriei grafurilor .
Declarație de probleme: Având în vedere un grafic nedirecționat, sarcina este de a determina dacă graficul conține un ciclu hamiltonian sau nu. Dacă conține, atunci tipărește calea.
Exemplu:
Recomandat: Vă rugăm să rezolvați problema PRACTICĂ mai întâi, înainte de a trece la soluție.Intrare: grafic[][] = {{0, 1, 0, 1, 0},{1, 0, 1, 1, 1},{0, 1, 0, 0, 1},{1, 1, 0, 0, 1},{0, 1, 1, 1, 0}}
Graficul de intrare[][]
cum functioneaza un calculatorIeșire: {0, 1, 2, 4, 3, 0}.
Intrare: grafic[][] = {{0, 1, 0, 1, 0},{1, 0, 1, 1, 1},{0, 1, 0, 0, 1},{1, 1, 0, 0, 0},{0, 1, 1, 0, 0}}
Graficul de intrare[][]
Ieșire: Soluția nu există
Algoritm naiv : Această problemă poate fi rezolvată folosind ideea de mai jos:
Generați toate configurațiile posibile de vârfuri și imprimați o configurație care satisface constrângerile date. Va fi n! (n factoriale) configurații. Deci complexitatea temporală generală a acestei abordări va fi PE!).
Ciclul Hamiltonian folosind Algoritmul de backtracking :
Creați o matrice de căi goală și adăugați vârf 0 la ea. Adăugați alte vârfuri, începând de la vârf 1 . Înainte de a adăuga un vârf, verificați dacă acesta este adiacent vârfului adăugat anterior și nu este deja adăugat. Dacă găsim un astfel de vârf, adăugăm vârful ca parte a soluției. Dacă nu găsim un vârf, ne întoarcem fals .
Ilustrații:
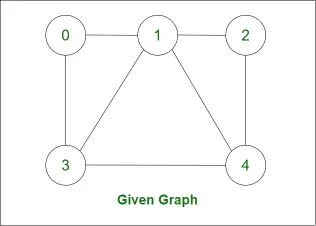
Să aflăm ciclul hamiltonian pentru următorul grafic:
- Începeți cu nodul 0.
- Aplicați DFS pentru a găsi calea hamiltoniană.
- Când ajunge la cazul de bază (de ex. numărul total de noduri parcurse == V (nod total) ):
- Verificați dacă nodul curent este vecin cu nodul de pornire.
- Ca nod 2 și nodul 0 nu sunt vecini unul cu celălalt, așa că întoarceți-vă de la ea.
Pornind de la nodul de pornire 0 apelând DFS
- Deoarece ciclul nu se găsește în calea {0, 3, 1, 4, 2}. Deci, reveniți de la nodul 2, nodul 4.
- Acum, explorați o altă opțiune pentru nodul 1 (adică nodul 2)
- Când atinge din nou condiția de bază, verificați ciclul hamiltonian
- Deoarece nodul 4 nu este vecinul nodului 0, din nou ciclul nu este găsit, apoi revine.
- Revenire de la nodul 4, nodul 2, nodul 1.
- Acum, explorați alte opțiuni pentru nodul 3.
Ciclul Hamiltonian
- Pe calea hamiltoniană {0,3,4,2,1,0} obținem ciclu, deoarece nodul 1 este vecinul nodului 0.
- Prin urmare, imprimați această cale ciclică.
- Acesta este ciclul nostru hamiltonian.
Mai jos este implementarea Backtracking pentru găsirea ciclului Hamiltonian:
C++ /* C++ program for solution of Hamiltonian Cycle problem using backtracking */ #include using namespace std; // Number of vertices in the graph #define V 5 void printSolution(int path[]); /* A utility function to check if the vertex v can be added at index 'pos' in the Hamiltonian Cycle constructed so far (stored in 'path[]') */ bool isSafe(int v, bool graph[V][V], int path[], int pos) { /* Check if this vertex is an adjacent vertex of the previously added vertex. */ if (graph [path[pos - 1]][ v ] == 0) return false; /* Check if the vertex has already been included. This step can be optimized by creating an array of size V */ for (int i = 0; i < pos; i++) if (path[i] == v) return false; return true; } /* A recursive utility function to solve hamiltonian cycle problem */ bool hamCycleUtil(bool graph[V][V], int path[], int pos) { /* base case: If all vertices are included in Hamiltonian Cycle */ if (pos == V) { // And if there is an edge from the // last included vertex to the first vertex if (graph[path[pos - 1]][path[0]] == 1) return true; else return false; } // Try different vertices as a next candidate // in Hamiltonian Cycle. We don't try for 0 as // we included 0 as starting point in hamCycle() for (int v = 1; v < V; v++) { /* Check if this vertex can be added // to Hamiltonian Cycle */ if (isSafe(v, graph, path, pos)) { path[pos] = v; /* recur to construct rest of the path */ if (hamCycleUtil (graph, path, pos + 1) == true) return true; /* If adding vertex v doesn't lead to a solution, then remove it */ path[pos] = -1; } } /* If no vertex can be added to Hamiltonian Cycle constructed so far, then return false */ return false; } /* This function solves the Hamiltonian Cycle problem using Backtracking. It mainly uses hamCycleUtil() to solve the problem. It returns false if there is no Hamiltonian Cycle possible, otherwise return true and prints the path. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ bool hamCycle(bool graph[V][V]) { int *path = new int[V]; for (int i = 0; i < V; i++) path[i] = -1; /* Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected */ path[0] = 0; if (hamCycleUtil(graph, path, 1) == false ) { cout << '
Solution does not exist'; return false; } printSolution(path); return true; } /* A utility function to print solution */ void printSolution(int path[]) { cout << 'Solution Exists:' ' Following is one Hamiltonian Cycle
'; for (int i = 0; i < V; i++) cout << path[i] << ' '; // Let us print the first vertex again // to show the complete cycle cout << path[0] << ' '; cout << endl; } // Driver Code int main() { /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) */ bool graph1[V][V] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 1}, {0, 1, 1, 1, 0}}; // Print the solution hamCycle(graph1); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) */ bool graph2[V][V] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 0}, {0, 1, 1, 0, 0}}; // Print the solution hamCycle(graph2); return 0; } // This is code is contributed by rathbhupendra> C++ #include using namespace std; int main() { cout << 'GFG!'; return 0; }> C /* C program for solution of Hamiltonian Cycle problem using backtracking */ #include // Number of vertices in the graph #define V 5 void printSolution(int path[]); /* A utility function to check if the vertex v can be added at index 'pos' in the Hamiltonian Cycle constructed so far (stored in 'path[]') */ int isSafe(int v, int graph[V][V], int path[], int pos) { /* Check if this vertex is an adjacent vertex of the previously added vertex. */ if (graph [ path[pos-1] ][ v ] == 0) return 0; /* Check if the vertex has already been included. This step can be optimized by creating an array of size V */ for (int i = 0; i < pos; i++) if (path[i] == v) return 0; return 1; } /* A recursive utility function to solve hamiltonian cycle problem */ int hamCycleUtil(int graph[V][V], int path[], int pos) { /* base case: If all vertices are included in Hamiltonian Cycle */ if (pos == V) { // And if there is an edge from the last included vertex to the // first vertex if ( graph[ path[pos-1] ][ path[0] ] == 1 ) return 1; else return 0; } // Try different vertices as a next candidate in Hamiltonian Cycle. // We don't try for 0 as we included 0 as starting point in hamCycle() for (int v = 1; v < V; v++) { /* Check if this vertex can be added to Hamiltonian Cycle */ if (isSafe(v, graph, path, pos)) { path[pos] = v; /* recur to construct rest of the path */ if (hamCycleUtil (graph, path, pos+1) == 1) return 1; /* If adding vertex v doesn't lead to a solution, then remove it */ path[pos] = -1; } } /* If no vertex can be added to Hamiltonian Cycle constructed so far, then return false */ return 0; } /* This function solves the Hamiltonian Cycle problem using Backtracking. It mainly uses hamCycleUtil() to solve the problem. It returns false if there is no Hamiltonian Cycle possible, otherwise return true and prints the path. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ int hamCycle(int graph[V][V]) { int path[V]; for (int i = 0; i < V; i++) path[i] = -1; /* Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected */ path[0] = 0; if ( hamCycleUtil(graph, path, 1) == 0 ) { printf('
Solution does not exist'); return 0; } printSolution(path); return 1; } /* A utility function to print solution */ void printSolution(int path[]) { printf ('Solution Exists:' ' Following is one Hamiltonian Cycle
'); for (int i = 0; i < V; i++) printf(' %d ', path[i]); // Let us print the first vertex again to show the complete cycle printf(' %d ', path[0]); printf('
'); } // driver program to test above function int main() { /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) */ int graph1[V][V] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 1}, {0, 1, 1, 1, 0}, }; // Print the solution hamCycle(graph1); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) */ int graph2[V][V] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 0}, {0, 1, 1, 0, 0}, }; // Print the solution hamCycle(graph2); return 0; }> Java /* Java program for solution of Hamiltonian Cycle problem using backtracking */ class HamiltonianCycle { final int V = 5; int path[]; /* A utility function to check if the vertex v can be added at index 'pos'in the Hamiltonian Cycle constructed so far (stored in 'path[]') */ boolean isSafe(int v, int graph[][], int path[], int pos) { /* Check if this vertex is an adjacent vertex of the previously added vertex. */ if (graph[path[pos - 1]][v] == 0) return false; /* Check if the vertex has already been included. This step can be optimized by creating an array of size V */ for (int i = 0; i < pos; i++) if (path[i] == v) return false; return true; } /* A recursive utility function to solve hamiltonian cycle problem */ boolean hamCycleUtil(int graph[][], int path[], int pos) { /* base case: If all vertices are included in Hamiltonian Cycle */ if (pos == V) { // And if there is an edge from the last included // vertex to the first vertex if (graph[path[pos - 1]][path[0]] == 1) return true; else return false; } // Try different vertices as a next candidate in // Hamiltonian Cycle. We don't try for 0 as we // included 0 as starting point in hamCycle() for (int v = 1; v < V; v++) { /* Check if this vertex can be added to Hamiltonian Cycle */ if (isSafe(v, graph, path, pos)) { path[pos] = v; /* recur to construct rest of the path */ if (hamCycleUtil(graph, path, pos + 1) == true) return true; /* If adding vertex v doesn't lead to a solution, then remove it */ path[pos] = -1; } } /* If no vertex can be added to Hamiltonian Cycle constructed so far, then return false */ return false; } /* This function solves the Hamiltonian Cycle problem using Backtracking. It mainly uses hamCycleUtil() to solve the problem. It returns false if there is no Hamiltonian Cycle possible, otherwise return true and prints the path. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ int hamCycle(int graph[][]) { path = new int[V]; for (int i = 0; i < V; i++) path[i] = -1; /* Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected */ path[0] = 0; if (hamCycleUtil(graph, path, 1) == false) { System.out.println('
Solution does not exist'); return 0; } printSolution(path); return 1; } /* A utility function to print solution */ void printSolution(int path[]) { System.out.println('Solution Exists: Following' + ' is one Hamiltonian Cycle'); for (int i = 0; i < V; i++) System.out.print(' ' + path[i] + ' '); // Let us print the first vertex again to show the // complete cycle System.out.println(' ' + path[0] + ' '); } // driver program to test above function public static void main(String args[]) { HamiltonianCycle hamiltonian = new HamiltonianCycle(); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) */ int graph1[][] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 1}, {0, 1, 1, 1, 0}, }; // Print the solution hamiltonian.hamCycle(graph1); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) */ int graph2[][] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 0}, {0, 1, 1, 0, 0}, }; // Print the solution hamiltonian.hamCycle(graph2); } } // This code is contributed by Abhishek Shankhadhar> Piton # Python program for solution of # hamiltonian cycle problem class Graph(): def __init__(self, vertices): self.graph = [[0 for column in range(vertices)] for row in range(vertices)] self.V = vertices ''' Check if this vertex is an adjacent vertex of the previously added vertex and is not included in the path earlier ''' def isSafe(self, v, pos, path): # Check if current vertex and last vertex # in path are adjacent if self.graph[ path[pos-1] ][v] == 0: return False # Check if current vertex not already in path for vertex in path: if vertex == v: return False return True # A recursive utility function to solve # hamiltonian cycle problem def hamCycleUtil(self, path, pos): # base case: if all vertices are # included in the path if pos == self.V: # Last vertex must be adjacent to the # first vertex in path to make a cycle if self.graph[ path[pos-1] ][ path[0] ] == 1: return True else: return False # Try different vertices as a next candidate # in Hamiltonian Cycle. We don't try for 0 as # we included 0 as starting point in hamCycle() for v in range(1,self.V): if self.isSafe(v, pos, path) == True: path[pos] = v if self.hamCycleUtil(path, pos+1) == True: return True # Remove current vertex if it doesn't # lead to a solution path[pos] = -1 return False def hamCycle(self): path = [-1] * self.V ''' Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected ''' path[0] = 0 if self.hamCycleUtil(path,1) == False: print ('Solution does not exist
') return False self.printSolution(path) return True def printSolution(self, path): print ('Solution Exists: Following', 'is one Hamiltonian Cycle') for vertex in path: print (vertex ) # Driver Code ''' Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) ''' g1 = Graph(5) g1.graph = [ [0, 1, 0, 1, 0], [1, 0, 1, 1, 1], [0, 1, 0, 0, 1,],[1, 1, 0, 0, 1], [0, 1, 1, 1, 0], ] # Print the solution g1.hamCycle(); ''' Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) ''' g2 = Graph(5) g2.graph = [ [0, 1, 0, 1, 0], [1, 0, 1, 1, 1], [0, 1, 0, 0, 1,], [1, 1, 0, 0, 0], [0, 1, 1, 0, 0], ] # Print the solution g2.hamCycle(); # This code is contributed by Divyanshu Mehta> C# // C# program for solution of Hamiltonian // Cycle problem using backtracking using System; public class HamiltonianCycle { readonly int V = 5; int []path; /* A utility function to check if the vertex v can be added at index 'pos'in the Hamiltonian Cycle constructed so far (stored in 'path[]') */ bool isSafe(int v, int [,]graph, int []path, int pos) { /* Check if this vertex is an adjacent vertex of the previously added vertex. */ if (graph[path[pos - 1], v] == 0) return false; /* Check if the vertex has already been included. This step can be optimized by creating an array of size V */ for (int i = 0; i < pos; i++) if (path[i] == v) return false; return true; } /* A recursive utility function to solve hamiltonian cycle problem */ bool hamCycleUtil(int [,]graph, int []path, int pos) { /* base case: If all vertices are included in Hamiltonian Cycle */ if (pos == V) { // And if there is an edge from the last included // vertex to the first vertex if (graph[path[pos - 1],path[0]] == 1) return true; else return false; } // Try different vertices as a next candidate in // Hamiltonian Cycle. We don't try for 0 as we // included 0 as starting point in hamCycle() for (int v = 1; v < V; v++) { /* Check if this vertex can be added to Hamiltonian Cycle */ if (isSafe(v, graph, path, pos)) { path[pos] = v; /* recur to construct rest of the path */ if (hamCycleUtil(graph, path, pos + 1) == true) return true; /* If adding vertex v doesn't lead to a solution, then remove it */ path[pos] = -1; } } /* If no vertex can be added to Hamiltonian Cycle constructed so far, then return false */ return false; } /* This function solves the Hamiltonian Cycle problem using Backtracking. It mainly uses hamCycleUtil() to solve the problem. It returns false if there is no Hamiltonian Cycle possible, otherwise return true and prints the path. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ int hamCycle(int [,]graph) { path = new int[V]; for (int i = 0; i < V; i++) path[i] = -1; /* Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected */ path[0] = 0; if (hamCycleUtil(graph, path, 1) == false) { Console.WriteLine('
Solution does not exist'); return 0; } printSolution(path); return 1; } /* A utility function to print solution */ void printSolution(int []path) { Console.WriteLine('Solution Exists: Following' + ' is one Hamiltonian Cycle'); for (int i = 0; i < V; i++) Console.Write(' ' + path[i] + ' '); // Let us print the first vertex again // to show the complete cycle Console.WriteLine(' ' + path[0] + ' '); } // Driver code public static void Main(String []args) { HamiltonianCycle hamiltonian = new HamiltonianCycle(); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) */ int [,]graph1= {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 1}, {0, 1, 1, 1, 0}, }; // Print the solution hamiltonian.hamCycle(graph1); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) */ int [,]graph2 = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 0}, {0, 1, 1, 0, 0}, }; // Print the solution hamiltonian.hamCycle(graph2); } } // This code contributed by Rajput-Ji> Javascript >>>PHP>>>
Ieșire Complexitatea timpului: O(N!), unde N este numărul de vârfuri.
Spațiu auxiliar: O(1), deoarece nu este folosit spațiu suplimentar. Notă: Codul de mai sus tipărește întotdeauna un ciclu care începe de la 0 . Punctul de pornire nu ar trebui să conteze, deoarece ciclul poate fi pornit din orice punct. Dacă doriți să schimbați punctul de plecare, ar trebui să faceți două modificări codului de mai sus.
Schimbați calea[0] = 0; la cale[0] = s ; Unde s este noua ta punct de start . De asemenea, schimbați bucla pentru (int v = 1; v