 #practiceLinkDiv { display: none !important; }
#practiceLinkDiv { display: none !important; }Având în vedere un set de puncte ca și o dreaptă ca ax+by+c = 0. Trebuie să găsim un punct pe o dreaptă dată pentru care suma distanțelor de la un set dat de puncte este minimă.
Exemplu:
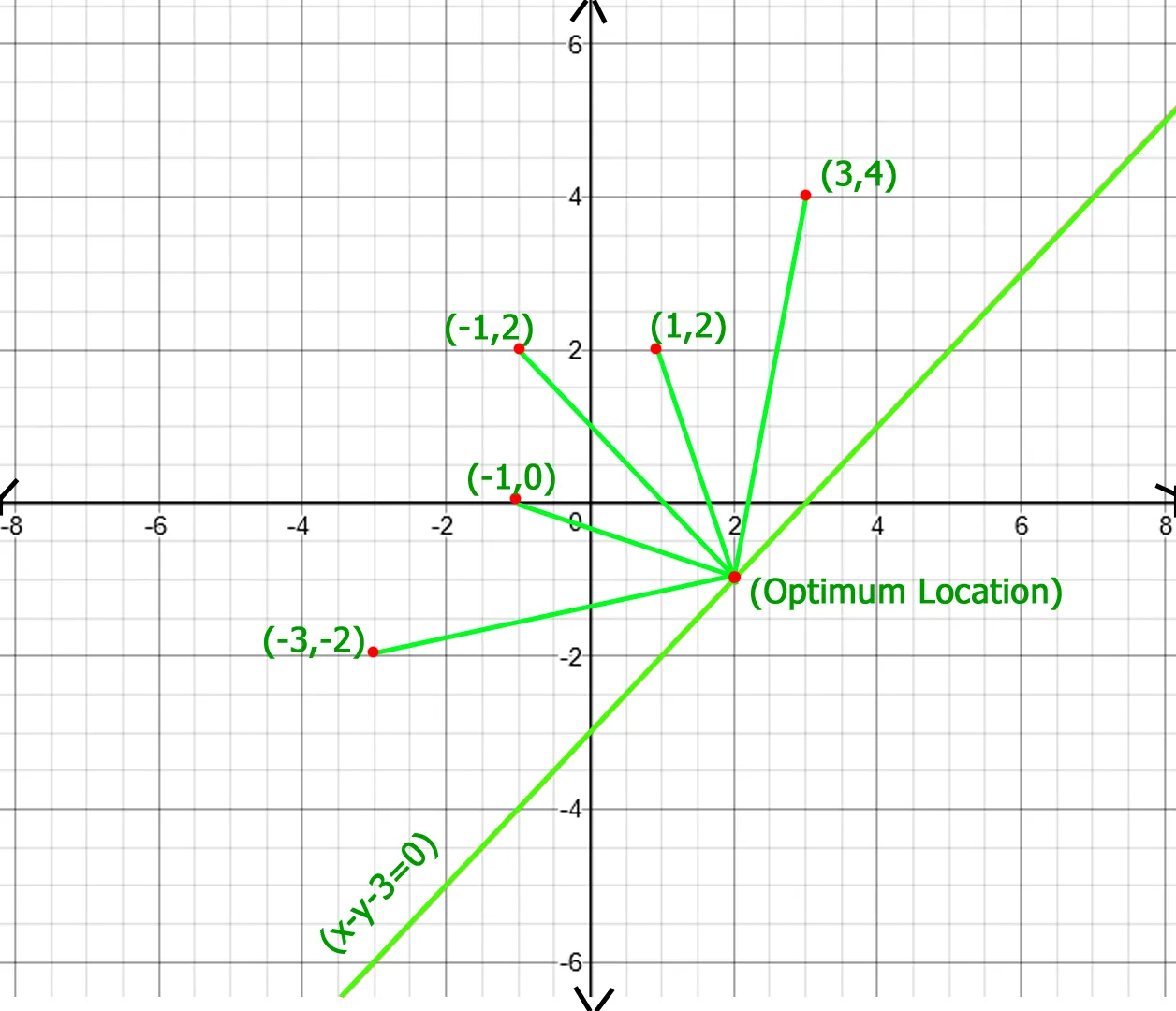
In above figure optimum location of point of x - y - 3 = 0 line is (2 -1) whose total distance with other points is 20.77 which is minimum obtainable total distance.Recommended Practice Locația optimă a punctului pentru a minimiza distanța totală Încearcă!
Dacă luăm un punct de pe o linie dată la o distanță infinită, atunci costul total al distanței va fi infinit acum, când deplasăm acest punct pe linie către puncte date, costul total al distanței începe să scadă și după un timp începe din nou să crească, care a ajuns la infinit la celălalt capăt infinit al liniei, astfel încât curba costului distanței arată ca o curbă U și trebuie să găsim valoarea de jos a acestei curbe U.
Deoarece curba U nu crește sau descrește în mod monoton, nu putem folosi căutarea binară pentru a găsi cel mai mic punct aici vom folosi căutarea ternară pentru a găsi cel mai jos punct căutarea ternară omite o treime din spațiul de căutare la fiecare iterație, puteți citi mai multe despre căutarea ternară Aici .
Deci, soluția procedează după cum urmează, începem cu inițializarea scăzută și înaltă ca unele valori cele mai mici și, respectiv, cele mai mari, apoi începem iterația în fiecare iterație, calculăm două medii mid1 și mid2 care reprezintă pozițiile de 1/3 și 2/3 în spațiul de căutare, calculăm distanța totală a tuturor punctelor cu mid1 și mid2 și actualizăm joasă sau mare comparând aceste distanțe, costă această iterație aproximativ egală și mai mare, până când această iterație continuă aproximativ egală.
C++// C/C++ program to find optimum location and total cost #include
// A Java program to find optimum location // and total cost class GFG { static double sq(double x) { return ((x) * (x)); } static int EPS = (int)(1e-6) + 1; static int N = 5; // structure defining a point static class point { int x y; point() {} public point(int x int y) { this.x = x; this.y = y; } }; // structure defining a line of ax + by + c = 0 form static class line { int a b c; public line(int a int b int c) { this.a = a; this.b = b; this.c = c; } }; // method to get distance of point (x y) from point p static double dist(double x double y point p) { return Math.sqrt(sq(x - p.x) + sq(y - p.y)); } /* Utility method to compute total distance all points when choose point on given line has x-coordinate value as X */ static double compute(point p[] int n line l double X) { double res = 0; // calculating Y of chosen point by line equation double Y = -1 * (l.c + l.a * X) / l.b; for (int i = 0; i < n; i++) res += dist(X Y p[i]); return res; } // Utility method to find minimum total distance static double findOptimumCostUtil(point p[] int n line l) { double low = -1e6; double high = 1e6; // loop until difference between low and high // become less than EPS while ((high - low) > EPS) { // mid1 and mid2 are representative x // co-ordiantes of search space double mid1 = low + (high - low) / 3; double mid2 = high - (high - low) / 3; double dist1 = compute(p n l mid1); double dist2 = compute(p n l mid2); // if mid2 point gives more total distance // skip third part if (dist1 < dist2) high = mid2; // if mid1 point gives more total distance // skip first part else low = mid1; } // compute optimum distance cost by sending average // of low and high as X return compute(p n l (low + high) / 2); } // method to find optimum cost static double findOptimumCost(int points[][] line l) { point[] p = new point[N]; // converting 2D array input to point array for (int i = 0; i < N; i++) p[i] = new point(points[i][0] points[i][1]); return findOptimumCostUtil(p N l); } // Driver Code public static void main(String[] args) { line l = new line(1 -1 -3); int points[][] = { { -3 -2 } { -1 0 } { -1 2 } { 1 2 } { 3 4 } }; System.out.println(findOptimumCost(points l)); } } // This code is contributed by Rajput-Ji
# A Python3 program to find optimum location # and total cost import math class Optimum_distance: # Class defining a point class Point: def __init__(self x y): self.x = x self.y = y # Class defining a line of ax + by + c = 0 form class Line: def __init__(self a b c): self.a = a self.b = b self.c = c # Method to get distance of point # (x y) from point p def dist(self x y p): return math.sqrt((x - p.x) ** 2 + (y - p.y) ** 2) # Utility method to compute total distance # all points when choose point on given # line has x-coordinate value as X def compute(self p n l x): res = 0 y = -1 * (l.a*x + l.c) / l.b # Calculating Y of chosen point # by line equation for i in range(n): res += self.dist(x y p[i]) return res # Utility method to find minimum total distance def find_Optimum_cost_untill(self p n l): low = -1e6 high = 1e6 eps = 1e-6 + 1 # Loop until difference between low # and high become less than EPS while((high - low) > eps): # mid1 and mid2 are representative x # co-ordiantes of search space mid1 = low + (high - low) / 3 mid2 = high - (high - low) / 3 dist1 = self.compute(p n l mid1) dist2 = self.compute(p n l mid2) # If mid2 point gives more total # distance skip third part if (dist1 < dist2): high = mid2 # If mid1 point gives more total # distance skip first part else: low = mid1 # Compute optimum distance cost by # sending average of low and high as X return self.compute(p n l (low + high) / 2) # Method to find optimum cost def find_Optimum_cost(self p l): n = len(p) p_arr = [None] * n # Converting 2D array input to point array for i in range(n): p_obj = self.Point(p[i][0] p[i][1]) p_arr[i] = p_obj return self.find_Optimum_cost_untill(p_arr n l) # Driver Code if __name__ == '__main__': obj = Optimum_distance() l = obj.Line(1 -1 -3) p = [ [ -3 -2 ] [ -1 0 ] [ -1 2 ] [ 1 2 ] [ 3 4 ] ] print(obj.find_Optimum_cost(p l)) # This code is contributed by Sulu_mufi
// C# program to find optimum location // and total cost using System; class GFG { static double sq(double x) { return ((x) * (x)); } static int EPS = (int)(1e-6) + 1; static int N = 5; // structure defining a point public class point { public int x y; public point() {} public point(int x int y) { this.x = x; this.y = y; } }; // structure defining a line // of ax + by + c = 0 form public class line { public int a b c; public line(int a int b int c) { this.a = a; this.b = b; this.c = c; } }; // method to get distance of // point (x y) from point p static double dist(double x double y point p) { return Math.Sqrt(sq(x - p.x) + sq(y - p.y)); } /* Utility method to compute total distance of all points when choose point on given line has x-coordinate value as X */ static double compute(point[] p int n line l double X) { double res = 0; // calculating Y of chosen point // by line equation double Y = -1 * (l.c + l.a * X) / l.b; for (int i = 0; i < n; i++) res += dist(X Y p[i]); return res; } // Utility method to find minimum total distance static double findOptimumCostUtil(point[] p int n line l) { double low = -1e6; double high = 1e6; // loop until difference between // low and high become less than EPS while ((high - low) > EPS) { // mid1 and mid2 are representative // x co-ordiantes of search space double mid1 = low + (high - low) / 3; double mid2 = high - (high - low) / 3; double dist1 = compute(p n l mid1); double dist2 = compute(p n l mid2); // if mid2 point gives more total distance // skip third part if (dist1 < dist2) high = mid2; // if mid1 point gives more total distance // skip first part else low = mid1; } // compute optimum distance cost by // sending average of low and high as X return compute(p n l (low + high) / 2); } // method to find optimum cost static double findOptimumCost(int[ ] points line l) { point[] p = new point[N]; // converting 2D array input to point array for (int i = 0; i < N; i++) p[i] = new point(points[i 0] points[i 1]); return findOptimumCostUtil(p N l); } // Driver Code public static void Main(String[] args) { line l = new line(1 -1 -3); int[ ] points = { { -3 -2 } { -1 0 } { -1 2 } { 1 2 } { 3 4 } }; Console.WriteLine(findOptimumCost(points l)); } } // This code is contributed by 29AjayKumar
<script> // A JavaScript program to find optimum location // and total cost function sq(x) { return x*x; } let EPS = (1e-6) + 1; let N = 5; // structure defining a point class point { constructor(xy) { this.x=x; this.y=y; } } // structure defining a line of ax + by + c = 0 form class line { constructor(abc) { this.a = a; this.b = b; this.c = c; } } // method to get distance of point (x y) from point p function dist(xyp) { return Math.sqrt(sq(x - p.x) + sq(y - p.y)); } /* Utility method to compute total distance all points when choose point on given line has x-coordinate value as X */ function compute(pnlX) { let res = 0; // calculating Y of chosen point by line equation let Y = -1 * (l.c + l.a * X) / l.b; for (let i = 0; i < n; i++) res += dist(X Y p[i]); return res; } // Utility method to find minimum total distance function findOptimumCostUtil(pnl) { let low = -1e6; let high = 1e6; // loop until difference between low and high // become less than EPS while ((high - low) > EPS) { // mid1 and mid2 are representative x // co-ordiantes of search space let mid1 = low + (high - low) / 3; let mid2 = high - (high - low) / 3; let dist1 = compute(p n l mid1); let dist2 = compute(p n l mid2); // if mid2 point gives more total distance // skip third part if (dist1 < dist2) high = mid2; // if mid1 point gives more total distance // skip first part else low = mid1; } // compute optimum distance cost by sending average // of low and high as X return compute(p n l (low + high) / 2); } // method to find optimum cost function findOptimumCost(pointsl) { let p = new Array(N); // converting 2D array input to point array for (let i = 0; i < N; i++) p[i] = new point(points[i][0] points[i][1]); return findOptimumCostUtil(p N l); } // Driver Code let l = new line(1 -1 -3); let points= [[ -3 -2 ] [ -1 0 ] [ -1 2 ] [ 1 2 ] [ 3 4 ]]; document.write(findOptimumCost(points l)); // This code is contributed by rag2127 </script>
Ieșire
20.7652
Complexitatea timpului: Pe2)
Spațiu auxiliar: Pe)
