Momentul de inerție este proprietatea unui corp aflat în mișcare de rotație. Momentul de inerție este proprietatea corpurilor de rotație care tinde să se opună modificării mișcării de rotație a corpului. Este similar cu inerția oricărui corp aflat în mișcare de translație. Matematic, momentul de inerție este dat ca suma produsului dintre masa fiecărei particule și pătratul distanței de la axa de rotație. Se măsoară în unitatea de kgm 2 .
Să aflăm despre momentul de inerție în detaliu în articolul de mai jos.
Cuprins
- Definiția momentului de inerție
- Formula momentului de inerție
- Factori care afectează momentul de inerție
- Cum se calculează momentul de inerție?
- Formula momentului de inerție pentru diferite forme
- Rază de girație
- Teoremele momentului de inerție
- Momente de inerție pentru diferite obiecte
Definiția momentului de inerție
Momentul de inerție este tendința unui corp în mișcare de rotație care se opune schimbării sale mișcare de rotație datorita fortelor externe. Momentul de inerție se comportă ca masă unghiulară și se numește inerție de rotație. Momentul de inerție este analog cu cel mecanic Inerţie a corpului.
MOI este definită ca fiind cantitatea exprimată prin suma produsului masa a fiecărei particule cu pătratul distanței sale față de axa de rotație pentru orice particulă care efectuează mișcarea de rotație.
Unitatea momentului de inerție
Momentul de inerție este o mărime scalară și unitatea SI a momentului de inerție este kgm 2 .
Formula dimensională a momentului de inerție
Deoarece momentul de inerție este dat ca produs al masei și pătratului distanței. Este formula dimensionala este dat de produsul formulei dimensionale a masei și pătratul formulei dimensionale a lungimii. Formula dimensională a momentului de inerție este: ML 2
Ce este inerția?
Inerția este proprietatea unei materie în virtutea căreia tinde să reziste schimbării stării de mișcare a acesteia. Aceasta înseamnă că un corp în repaus încearcă să rămână în repaus și să reziste oricărei forțe care încearcă să-l aducă în mișcare, iar un corp în mișcare încearcă să continue în mișcare și să reziste oricărei forțe care încearcă să-l aducă să-și schimbe amploarea mișcării. În ceea ce privește cantitatea, este egală cu forța maximă care încearcă să-și schimbe starea mişcare .
Află mai multe despre Inerţie .
Formula momentului de inerție
Momentul de inerție este a cantitatea scalară . Matematic, produsul dintre pătratul masei unei particule și distanța de la axa de rotație se numește momentul de inerție al particulei în jurul axei de rotație.
Formula generală pentru găsirea momentului de inerție al oricărui obiect este:
eu = dl 2
Unde,
m este masa obiectului”
r este distanța de la axa de rotație
Pentru un corp format din particule continue infinitezimal mici, forma integrală a momentului de inerție este utilizată pentru a calcula momentul de inerție.
I = ∫dI
eu =
int_{0}^{M} r^2 dm
Momentul de inerție al unui sistem de particule
Momentul de inerție al unui sistem de particule este dat de formula:
I = ∑m i r i 2
Unde,
r i este distanța perpendiculară a ithparticulă din axă
m i este masa lui ithparticulă
Ecuația de mai sus a momentului de inerție arată că momentul de inerție pentru un sistem de particule este egal cu suma produsului dintre masa fiecăreia și pătratul distanței de la axa de rotație a fiecărei particule.
Pentru figura de mai jos,
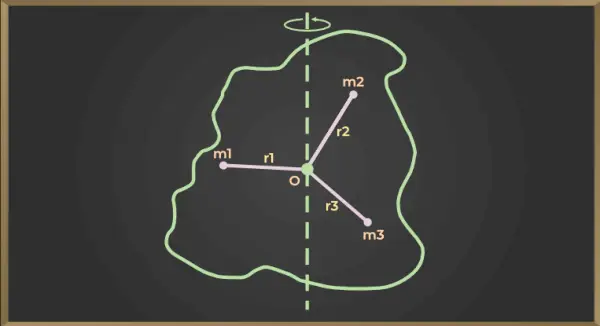
Momentul de inerție al primei particule = m1×r12
Momentul de inerție al celei de-a doua particule = m2×r22
Momentul de inerție al celei de-a treia particule = m3×r32
În mod similar,
Momentul de inerție al lui nthparticulă = mn×rn2
Acum momentul de inerție al întregului corp față de axa de rotație AB va fi egală cu suma momentului de inerție al tuturor particulelor, deci
I = m1×r12+ m2×r22+ m3×r32+……+mn×rn2
ce este cablat automat în java
I = Σm i ×r i 2
Unde,
eu reprezintă momentul de inerție al corpului față de axa de rotație
m i este masa lui ithparticule,
r i este raza lui ithparticulă
S reprezintă suma.
Din ecuație, putem spune că momentul de inerție al unui corp față de o axă fixă este egal cu suma produsului dintre masa fiecărei particule din acel corp și pătratul distanței sale perpendiculare față de axa fixă.
Factori care afectează momentul de inerție
Momentul de inerție al oricărui obiect depinde de următoarele valori:
- Forma și dimensiunea obiectului
- Densitatea materialului obiectului
- Axa de rotație
Cum se calculează momentul de inerție?
Sunt obișnuite mai multe moduri calculați momentul de inerție a oricărui obiect rotativ.
- Pentru obiectele uniforme, momentul de inerție se calculează luând produsul masei sale cu pătratul distanței față de axa de rotație (r2).
- Pentru obiectele neuniforme, calculăm momentul de inerție luând suma produsului maselor punctuale individuale la fiecare rază diferită pentru aceasta formula utilizată este
I = ∑m i r i 2
Formula momentului de inerție pentru diferite forme
Acest tabel discută expresiile pentru momentul de inerție pentru unele obiecte simetrice împreună cu axa lor de rotație:

| Obiect | Axă | Exprimarea momentului de inerție |
|---|---|---|
| Cilindru gol cu pereți subțiri | Central | eu = dl2 |
| Inel subțire | Diametru | I = 1/2 dl2 |
| Inel inelar sau cilindru gol | Central | I = 1/2 M(r22+ r12) |
| Cilindru solid | Central | I = 1/2 dl2 |
| Disc uniform | Diametru | I = 1/4 dl2 |
| Sferă goală | Central | I = 2/3 dl2 |
| Sferă solidă | Central | I = 2/5 dl2 |
| Înveliș sferic simetric uniform | Central | |
| Placă uniformă sau paralelepiped dreptunghiular | Central | I = 1/12 M(a2+ b2) |
| Tijă subțire | Central | I = 1/12 dl2 |
| Tijă subțire | La Capătul Rodului | I = 1/3 dl2 |
Rază de girație
The Rază de girație a unui corp este definită ca distanța perpendiculară de la axa de rotație la punctul de masă a cărui masă este egală cu masa întregului corp și momentul de inerție este egal cu momentul real de inerție al obiectului așa cum a fost. presupunând că masa totală a corpului este concentrată acolo. Este o distanta imaginara. Raza de rotație este notată cu K.
Dacă masa și raza de rotație a corpului sunt M și respectiv K, atunci momentul de inerție al unui corp este
I = MK 2 ……(1)
Astfel, raza de rotație a unui corp este perpendiculară pe axa de rotație al cărei pătrat înmulțit cu masa acelui corp dă momentul de inerție al acelui corp în jurul acelei axe.
Din nou prin ecuația (1), K2= I/M
K = √(I/m)
python rstrip
Astfel, raza de rotație a unui corp în jurul unei axe este egală cu rădăcina pătrată a raportului corpului în jurul acelei axe.
Teoremele momentului de inerție
Există două tipuri de teoreme care sunt foarte importante în ceea ce privește momentul de inerție:
- Teorema axei paralele
- Teorema axei perpendiculare
Teorema axei perpendiculare
Teorema axei perpendiculare afirmă că suma momentului de inerție al unui corp în jurul a două axe reciproc perpendiculare situate în planul unui corp este egală cu momentul de inerție al corpului în jurul celei de-a treia axe care este perpendiculară pe cele două axe și trece prin punctul lor. de intersectie.

În figura de mai sus, BOU și LTD sunt două axe în planul corpului care sunt perpendiculare una pe cealaltă. A treia axă este OZ care este perpendicular pe planul corpului și trece prin punctul de intersecție al BOU și LTD topoare. Dacă eu X , eu și , și eu Cu sunt momentele de inerție ale corpului față de axă BOU , LTD , și OZ respectiv axe, apoi conform acestei teoreme
eu X + eu și = eu Cu
Teorema axei paralele
Conform Teorema axei paralele , momentul de inerție al unui corp în jurul unei axe date este suma momentului de inerție în jurul unei axe care trece prin centrul de masă al acelui corp și produsul dintre pătratul masei corpului și distanța perpendiculară dintre două axe.

În figura de mai sus, trebuie să găsim momentul de inerție al eu O a corpului care trece prin punct O și în jurul axei perpendiculare pe plan, în timp ce momentul de inerție al corpului trece prin centrul de masă C iar în jurul unei axe paralele cu axa dată este eu C , apoi conform acestei teoreme
eu O = eu C + Ml 2
Unde
M este masa întregului corp
l este distanța perpendiculară dintre două axe.
Momente de inerție pentru diferite obiecte
Momentul de inerție al diferitelor obiecte este discutat mai jos în acest articol
Momentul de inerție al unei plăci dreptunghiulare
Dacă masa plăcii este M, lungimea l și lățimea b, atunci momentul de inerție trece prin centrul de greutate și în jurul unei axe perpendiculare pe planul plăcii.

I = M(l 2 + b 2 / 12)
Momentul de inerție al unui disc
Dacă discul are o masă M și o rază r, atunci momentul de inerție în jurul axei geometrice a discului este

I = 1/2 (dl 2 )
Momentul de inerție al unei tije
Dacă masa tijei este M și lungimea este l, atunci momentul de inerție în jurul axei perpendiculare pe lungimea tijei și care trece prin centrul său de greutate

I = ML 2 /12
Momentul de inerție al unui cerc
Dacă masa inelului este M și raza inelului este r, atunci momentul de inerție în jurul axei care trece perpendicular pe centrul inelului este

eu = dl 2
Momentul de inerție al unei sfere
Dacă o sferă solidă are o masă de M și o rază de r, atunci momentul de inerție în jurul diametrului său este

I = 2/5Mr 2
Momentul de inerție al cilindrului solid
Momentul de inerție al unui cilindru solid cu raza „R” și masa M este dat de

I = 1/2MR 2
Momentul de inerție al cilindrului gol
Un cilindru tubular are două raze și anume raza interioară și raza externă. Momentul de inerție al unui cilindru gol cu masa M, raza externă R1, și raza internă R2este dat ca

I = 1/2M(R 1 2 + R 2 2 )
Momentul de inerție al sferei solide
Momentul de inerție al unei sfere solide de masă „M” și rază „R” este dat ca

I = 2/5MR 2
Momentul de inerție al sferei goale
Momentul de inerție al unei sfere goale de masă M și rază „R” este dat ca

I = 2/3MR 2
Momentul de inerție al inelului
Momentul de inerție al unui inel este dat pentru două cazuri când axa de rotație trece prin centru și când axa de rotație trece prin diametru.
Momentul de inerție al inelului în jurul axei care trece prin centru este dat de
convertiți șirul în int

I = MR 2
Momentul de inerție al inelului în jurul axei care trece prin diametru este dat de

eu = dl 2 /2
Momentul de inerție al pătratului
Momentul de inerție al pătratului laturii „a” este dat ca

I = a 4 /12
Momentul de inerție al unei plăci pătrate a laturii cu lungimea „l” și masa M este dat ca
I = 1/6ML 2
Momentul de inerție al triunghiului
Momentul de inerție al unui triunghi este dat pentru 3 situații, prima, când axa trece prin centru, a doua când axa trece prin bază și a treia când axa este perpendiculară pe bază. Să vedem formula pentru ei unul câte unul. Pentru un triunghi cu baza „b” și înălțimea „h”, formula momentului de inerție este dată după cum urmează

Când axa trece prin Centroid
I = bh 3 /36
Când axa trece prin bază
I = bh 3 /12
Când axa este perpendiculară pe bază
I = (hb/36)(b 2 – b 1 b + b 1 2 )
Diferența dintre momentul de inerție și inerția
Diferența dintre inerție și momentul de inerție este tabelată mai jos:
| Da nu. | Inerţie | Moment de inerție |
|---|---|---|
| 1. | Importanța sa este în mișcarea liniară. | Importanța sa este în mișcarea de rotație. |
| 2. | Este acea proprietate a unui obiect care se opune schimbării stării obiectului în mișcare liniară. | Momentul de inerție este acea proprietate a unui obiect care se opune schimbării stării obiectului în mișcare de rotație. |
| 3. | Inerția unui obiect depinde doar de masa acestuia. | Momentul de inerție al unui obiect depinde de masa lui și de distribuția sa în raport cu axa de rotație. |
| 4. | Inerția unui obiect este fixă. | Momentul de inerție al unui obiect variază în funcție de diferite axe de rotație. |
Energia cinetică a corpului în rotație
Să presupunem un corp de masă „m” care se rotește cu viteza v la o distanță „r” de axa de rotație. Viteza sa unghiulară este dată de ω = v/r apoi v = rω. Acum știm că Energie kinetică a unui corp este dat de
KE = 1/2mv 2
⇒ KE = 1/2m(rω)2
⇒ KE = 1/2mr2Oh2
⇒ KE = 1/2Iω 2
Prin urmare, energia cinetică a unui corp în rotație este dată de jumătate din produsul momentului de inerție și viteză unghiulară a corpului. Se mai numește și energia cinetică a corpului în rotație Energie cinetică de rotație . Formula Energiei Cinetice de Rotație este dată ca
KE = 1/2Iω 2
Momentul de inerție (I) este independent de viteza unghiulară a corpului. Este o funcție a masei corpului în rotație și a distanței corpului față de axa de rotație. Prin urmare, observăm că mișcarea unghiulară este analogă mișcării liniare, ceea ce înseamnă că semnificația momentului de inerție este că dă o idee despre modul în care masele sunt distribuite la distanțe diferite față de axa de rotație într-un corp în rotație.
Aplicarea momentului de inerție
Moment of Inertia are diverse aplicații, dintre care unele sunt discutate mai jos:
- Datorită momentului de inerție mai mare, pământul se rotește pe axa sa cu aceeași viteză unghiulară.
- O mică roată mobilă este plasată sub motorul de joacă pentru copii. După frecarea acestei roți cu pământul și părăsirea motorului, din cauza momentului de inerție al roții, motorul continuă să funcționeze ceva timp.
- Fiecare motor constă dintr-o roată mare și grea atașată de arbore, cu cea mai mare parte a masei pe circumferință. Prin urmare, momentul său de inerție este ridicat. Această roată se numește volantă. Cuplul care antrenează arborele motorului continuă să crească. Prin urmare, rotația arborelui poate să nu fie uniformă, dar datorită prezenței unei roți în mișcare cu mai multă inerție, arborele continuă să se rotească cu o viteză aproape uniformă.
- În roata cărucioarelor cu boi, ricișelor, scuterelor, bicicletelor etc., cea mai mare parte a masei este concentrată pe cercul sau marginea acesteia. acest cerc sau rutină este atașat de axa roții prin spițe rigide. Făcând acest lucru, momentul său de inerție crește. Prin urmare, atunci când picioarele se opresc în mișcare în timpul mersului cu bicicleta, roata continuă să se învârtească pentru o perioadă de timp.
De asemenea, verifica
- Cinematica mișcării de rotație
- Mișcarea unui corp rigid
- Mișcare de rulare
Exemple rezolvate pe momente de inerție
Exemplul 1: Un corp cu o masă de 500 g se rotește în jurul unei axe. distanța centrului de masă al corpului față de axa de rotație este de 1,2 m. afla momentul de inertie al corpului fata de axa de rotatie.
Soluţie:
Având în vedere că M = 500 g = 0,5 kg, r = 1,2 m.
Evident, se poate presupune că întreaga masă a unui corp este plasată în centrul său de masă. Apoi momentul de inerție al corpului față de axa de rotație.
eu = dl2
I = 0,5 × (1,2)2
I = 0,72 kg m2
Exemplul 2: Raza de rotație în jurul unei axe aflate la 12 cm de centrul de masă a unui corp cu masa de 1,2 kg este de 13 cm. Calculați raza de revoluție și momentul de inerție în jurul unei axe care trece prin centrul de masă.
Soluţie:
Având în vedere că, M = 1,0 kg, K = 13 cm, l = 12 cm, KCM= ?, euCM= ?
Din teorema axei paralele I = ICM+ Ml2
K2= KCM2+ l2
sau KCM2= K2– l2
KCM2 = (13)2– (12)2= 25
KCM= 5
Acum, momentul de inerție ICM= MKCM2
euCM= 1,0 × (0,05)2= 2,5 × 10-3kg m2
Exemplul 3: Un corp cu o masă de 0,1 kg se rotește în jurul unei axe. dacă distanța centrului de masă al corpului față de axa de rotație este de 0,5 m, atunci găsiți momentul de inerție al corpului.
Soluţie:
Având în vedere că, M = 0,1 kg și r = 0,5 m
deci eu = dl2
I = 0,1 × (0,5)2
I = 0,025 kg m2
Exemplul 4: Momentul de inerție al inelelor în jurul unei axe care trece prin centrul acesteia perpendicular pe planul inelului circular este de 200 gm cm 2 . Care va fi momentul de inerție față de diametrul său?
Soluţie:
Momentul de inerție al unui inel circular în jurul unei axe care trece printr-un alt centru perpendicular pe planul său
DOMNUL2= 200 gm cm2
Moment de inerție aproape de diametru
= 1/2 MR2
= 1/2 × 200 = 100 gm cm2
Întrebări frecvente despre momentele de inerție
Cum se calculează momentul de inerție?
Formula de bază pentru găsirea momentului de inerție al oricărui obiect uniform este:
eu = dl 2
Unde,
m este masa obiectului”
r este distanța de la axa de rotațievariabilă globală javascript
Cum se calculează momentul de inerție al unui fascicul?
Momentul de inerție al unui fascicul de-a lungul centrului și a axei orizontale față de acesta este calculat folosind formula,
I = ML 2 / 12
De ce depinde momentul de inerție al unui corp?
Momentul de inerție al oricărui obiect depinde de factorii menționați mai jos:
- Masa trupului,
- Axa de rotație
- Forma și dimensiunea obiectului
Care este unitatea momentului de inerție?
Unitatea de măsură a momentului de inerție este Kgm 2
Momentul de inerție poate fi negativ?
Nu, momentul de inerție nu poate fi niciodată negativ.
Ce este momentul de inerție al masei?
Momentul de inerție al masei este măsurarea rezistenței unui corp la schimbarea momentului sau direcției sale unghiulare. Momentul de inerție al masei pentru o masă punctuală este dat de I = mr2iar pentru sistemul de particule, momentul de inerție al masei este dat ca I = Σimiri2
Ce este momentul de inerție al zonei?
Momentul de inerție al zonei este proprietatea unui plan de formă 2D care arată modul în care punctele sunt dispersate în raport cu o axă arbitrară într-un plan. Momentul de inerție al zonei este, de asemenea, cunoscut sub numele de al doilea moment al ariei sau al momentului pătratic al ariei. Formula pentru momentul de inerție al zonei în planul xy este dată ca IX y= ∫xy dxdxy = ∫xy dA
