Regresie logistică este o algoritm de învățare automată supravegheat folosit pentru sarcini de clasificare unde scopul este de a prezice probabilitatea ca o instanță să aparțină sau nu unei clase date. Regresia logistică este un algoritm statistic care analizează relația dintre doi factori de date. Articolul explorează elementele fundamentale ale regresiei logistice, tipurile și implementările acesteia.
Cuprins
- Ce este regresia logistică?
- Funcția logistică – Funcția sigmoidă
- Tipuri de regresie logistică
- Ipoteze ale regresiei logistice
- Cum funcționează regresia logistică?
- Implementarea codului pentru regresia logistică
- Compensație precizie-rechemare în setarea pragului de regresie logistică
- Cum se evaluează modelul de regresie logistică?
- Diferențele dintre regresia liniară și cea logistică
Ce este regresia logistică?
Regresia logistică este folosită pentru binar clasificare unde folosim funcția sigmoidă , care ia intrarea ca variabile independente și produce o valoare de probabilitate între 0 și 1.
De exemplu, avem două clase Clasa 0 și Clasa 1 dacă valoarea funcției logistice pentru o intrare este mai mare de 0,5 (valoare de prag), atunci aceasta aparține clasei 1, altfel aparține clasei 0. Se numește regresie deoarece este prelungirea lui regresie liniara dar este folosit mai ales pentru probleme de clasificare.
Puncte cheie:
- Regresia logistică prezice rezultatul unei variabile dependente categorice. Prin urmare, rezultatul trebuie să fie o valoare categorică sau discretă.
- Poate fi Da sau Nu, 0 sau 1, adevărat sau Fals etc., dar în loc să dea valoarea exactă ca 0 și 1, oferă valorile probabilistice care se află între 0 și 1.
- În regresia logistică, în loc să potrivim o linie de regresie, potrivim o funcție logistică în formă de S, care prezice două valori maxime (0 sau 1).
Funcția logistică – Funcția sigmoidă
- Funcția sigmoidă este o funcție matematică utilizată pentru a mapa valorile prezise la probabilități.
- Mapează orice valoare reală într-o altă valoare într-un interval de 0 și 1. Valoarea regresiei logistice trebuie să fie între 0 și 1, care nu poate depăși această limită, deci formează o curbă ca forma S.
- Curba formei S se numește funcție sigmoidă sau funcție logistică.
- În regresia logistică, folosim conceptul de valoare de prag, care definește probabilitatea fie 0, fie 1. Cum ar fi valorile peste valoarea pragului tind la 1, iar o valoare sub valorile pragului tinde spre 0.
Tipuri de regresie logistică
Pe baza categoriilor, regresia logistică poate fi clasificată în trei tipuri:
- Binom: În regresia logistică binomială, pot exista doar două tipuri posibile de variabile dependente, cum ar fi 0 sau 1, Reușit sau Eșuat etc.
- Multinom: În regresia logistică multinomială, pot exista 3 sau mai multe tipuri posibile neordonate ale variabilei dependente, cum ar fi pisică, câine sau oaie
- Ordinal: În regresia logistică ordinală, pot exista 3 sau mai multe tipuri posibile ordonate de variabile dependente, cum ar fi scăzut, mediu sau ridicat.
Ipoteze ale regresiei logistice
Vom explora ipotezele regresiei logistice, deoarece înțelegerea acestor ipoteze este importantă pentru a ne asigura că folosim aplicarea adecvată a modelului. Ipotezele includ:
- Observații independente: Fiecare observație este independentă de cealaltă. ceea ce înseamnă că nu există nicio corelație între variabilele de intrare.
- Variabile dependente binare: se presupune că variabila dependentă trebuie să fie binară sau dihotomică, ceea ce înseamnă că poate lua doar două valori. Pentru mai mult de două categorii sunt utilizate funcțiile SoftMax.
- Relația de liniaritate între variabilele independente și șansele logaritmice: relația dintre variabilele independente și șansele logaritmice ale variabilei dependente ar trebui să fie liniară.
- Fără valori aberante: nu ar trebui să existe valori aberante în setul de date.
- Dimensiunea mare a eșantionului: dimensiunea eșantionului este suficient de mare
Terminologii implicate în regresia logistică
Iată câțiva termeni comuni implicați în regresia logistică:
- Variabile independente: Caracteristicile de intrare sau factorii predictori aplicați predicțiilor variabilei dependente.
- Variabilă dependentă: Variabila țintă într-un model de regresie logistică, pe care încercăm să o prezicem.
- Funcția logistică: Formula utilizată pentru a reprezenta modul în care variabilele independente și dependente se relaționează între ele. Funcția logistică transformă variabilele de intrare într-o valoare de probabilitate între 0 și 1, care reprezintă probabilitatea ca variabila dependentă să fie 1 sau 0.
- Cote: Este raportul dintre ceva ce se întâmplă și ceva care nu se întâmplă. este diferită de probabilitate, deoarece probabilitatea este raportul dintre ceva ce se întâmplă și tot ceea ce ar putea avea loc.
- Log-cote: Log-odds, cunoscută și sub numele de funcție logit, este logaritmul natural al cotelor. În regresia logistică, cotele logarite ale variabilei dependente sunt modelate ca o combinație liniară a variabilelor independente și interceptarea.
- Coeficient: Parametrii estimați ai modelului de regresie logistică arată modul în care variabilele independente și dependente se relaționează între ele.
- Intercepta: Un termen constant în modelul de regresie logistică, care reprezintă șansele logaritmice atunci când toate variabilele independente sunt egale cu zero.
- Estimarea probabilității maxime : Metoda utilizată pentru estimarea coeficienților modelului de regresie logistică, care maximizează probabilitatea de a observa datele date modelului.
Cum funcționează regresia logistică?
Modelul de regresie logistică transformă regresie liniara funcția de ieșire a valorii continue într-o ieșire a valorii categorice folosind o funcție sigmoidă, care mapează orice set cu valori reale de variabile independente introduse într-o valoare între 0 și 1. Această funcție este cunoscută sub numele de funcție logistică.
Fie caracteristicile de intrare independente:
iar variabila dependentă este Y având doar valoare binară, adică 0 sau 1.
apoi, aplicați funcția multiliniară la variabilele de intrare X.
Aici
orice am discutat mai sus este regresie liniara .
Funcția sigmoidă
Acum folosim funcția sigmoidă unde intrarea va fi z și găsim probabilitatea între 0 și 1. adică y prezis.
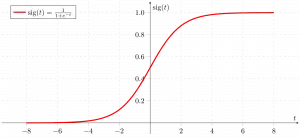
Funcția sigmoidă
După cum se arată mai sus, funcția sigmoidă a figurii convertește datele variabile continue în probabilitate adică între 0 și 1.
sigma(z) tinde spre 1 caz ightarrowinfty sigma(z) tinde spre 0 caz ightarrow-infty sigma(z) este întotdeauna mărginită între 0 și 1
unde probabilitatea de a fi o clasă poate fi măsurată ca:
Ecuația de regresie logistică
Ciudat este raportul dintre ceva ce se întâmplă și ceva care nu se întâmplă. este diferită de probabilitate, deoarece probabilitatea este raportul dintre ceva ce se întâmplă și tot ceea ce ar putea avea loc. asa de ciudat va fi:
Aplicarea logului natural pe impar. atunci log impar va fi:
atunci ecuația finală de regresie logistică va fi:
Funcția de probabilitate pentru regresia logistică
Probabilitățile prezise vor fi:
- pentru y=1 Probabilitățile prezise vor fi: p(X;b,w) = p(x)
- pentru y = 0 Probabilitățile prezise vor fi: 1-p(X;b,w) = 1-p(x)
Luați bușteni naturali pe ambele părți
Gradient al funcției de log-probabilitate
Pentru a găsi estimările de probabilitate maximă, diferențiam w.r.t w,
Implementarea codului pentru regresia logistică
Regresie binomială logistică:
Variabila țintă poate avea doar 2 tipuri posibile: 0 sau 1 care poate reprezenta câștig vs pierdere, trece vs eșec, mort vs viu etc., în acest caz, sunt utilizate funcții sigmoide, care este deja discutat mai sus.
Importarea bibliotecilor necesare pe baza cerințelor modelului. Acest cod Python arată cum să utilizați setul de date despre cancerul de sân pentru a implementa un model de regresie logistică pentru clasificare.
Python3 # import the necessary libraries from sklearn.datasets import load_breast_cancer from sklearn.linear_model import LogisticRegression from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score # load the breast cancer dataset X, y = load_breast_cancer(return_X_y=True) # split the train and test dataset X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, random_state=23) # LogisticRegression clf = LogisticRegression(random_state=0) clf.fit(X_train, y_train) # Prediction y_pred = clf.predict(X_test) acc = accuracy_score(y_test, y_pred) print('Logistic Regression model accuracy (in %):', acc*100)> Ieșire :
Precizia modelului de regresie logistică (în %): 95,6140350877193
Regresie logistică multinomială:
Variabila țintă poate avea 3 sau mai multe tipuri posibile care nu sunt ordonate (adică tipurile nu au semnificație cantitativă), cum ar fi boala A vs boala B vs boala C.
În acest caz, funcția softmax este utilizată în locul funcției sigmoid. Funcția Softmax pentru clasele K vor fi:
Aici, K reprezintă numărul de elemente din vectorul z, iar i, j iterează peste toate elementele din vector.
Atunci probabilitatea pentru clasa c va fi:
În regresia logistică multinomială, variabila de ieșire poate avea mai mult de două ieșiri discrete posibile . Luați în considerare setul de date cu cifre.
Python3 from sklearn.model_selection import train_test_split from sklearn import datasets, linear_model, metrics # load the digit dataset digits = datasets.load_digits() # defining feature matrix(X) and response vector(y) X = digits.data y = digits.target # splitting X and y into training and testing sets X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=1) # create logistic regression object reg = linear_model.LogisticRegression() # train the model using the training sets reg.fit(X_train, y_train) # making predictions on the testing set y_pred = reg.predict(X_test) # comparing actual response values (y_test) # with predicted response values (y_pred) print('Logistic Regression model accuracy(in %):', metrics.accuracy_score(y_test, y_pred)*100)> Ieșire:
Precizia modelului de regresie logistică (în %): 96,52294853963839
Cum se evaluează modelul de regresie logistică?
Putem evalua modelul de regresie logistică folosind următoarele metrici:
- Precizie: Precizie furnizează proporția de instanțe clasificate corect.
Accuracy = frac{True , Positives + True , Negatives}{Total}
- Precizie: Precizie se concentrează pe acuratețea predicțiilor pozitive.
Precision = frac{True , Positives }{True, Positives + False , Positives}
- Rechemare (sensibilitate sau rata pozitivă adevărată): Amintiți-vă măsoară proporția de cazuri pozitive prezise corect dintre toate cazurile pozitive reale.
Recall = frac{ True , Positives}{True, Positives + False , Negatives}
- Scor F1: Scorul F1 este mijlocul armonic al preciziei și reamintirii.
F1 , Score = 2 * frac{Precision * Recall}{Precision + Recall}
- Zona sub curba caracteristică de funcționare a receptorului (AUC-ROC): Curba ROC grafică rata pozitivă adevărată față de rata pozitivă fals la diferite praguri. AUC-ROC măsoară aria de sub această curbă, oferind o măsură agregată a performanței unui model la diferite praguri de clasificare.
- Zona sub curba de precizie-rechemare (AUC-PR): Similar cu AUC-ROC, AUC-PR măsoară aria de sub curba de precizie-rechemare, oferind un rezumat al performanței unui model în diferite compromisuri de precizie-rechemare.
Compensație precizie-rechemare în setarea pragului de regresie logistică
Regresia logistică devine o tehnică de clasificare numai atunci când este adus în imagine un prag de decizie. Setarea valorii prag este un aspect foarte important al regresiei logistice și depinde de problema de clasificare în sine.
Decizia privind valoarea pragului este afectată în mare măsură de valorile lui precizie și reamintire. În mod ideal, dorim ca atât precizia, cât și reamintirea să fie 1, dar acest lucru este rareori cazul.
În cazul unui Compensație precizie-rechemare , folosim următoarele argumente pentru a decide asupra pragului:
- Precizie scăzută/Reamintire ridicată: În aplicațiile în care dorim să reducem numărul de false negative fără a reduce neapărat numărul de fals pozitive, alegem o valoare de decizie care are o valoare scăzută de Precizie sau o valoare mare de Recall. De exemplu, într-o aplicație de diagnosticare a cancerului, nu dorim ca niciun pacient afectat să fie clasificat ca neafectat fără să acordăm prea multă atenție dacă pacientul este diagnosticat în mod greșit cu cancer. Acest lucru se datorează faptului că absența cancerului poate fi detectată de alte boli medicale, dar prezența bolii nu poate fi detectată la un candidat deja respins.
- Precizie ridicată/reamintire scăzută: În aplicațiile în care dorim să reducem numărul de false pozitive fără a reduce neapărat numărul de fals negative, alegem o valoare de decizie care are o valoare mare a Preciziei sau o valoare scăzută a Recall. De exemplu, dacă clasificăm clienții dacă vor reacționa pozitiv sau negativ la o reclamă personalizată, dorim să fim absolut siguri că clientul va reacționa pozitiv la reclamă, deoarece, în caz contrar, o reacție negativă poate provoca o pierdere a vânzărilor potențiale din partea client.
Diferențele dintre regresia liniară și cea logistică
Diferența dintre regresia liniară și regresia logistică este că rezultatul regresiei liniare este valoarea continuă care poate fi orice, în timp ce regresia logistică prezice probabilitatea ca o instanță să aparțină sau nu unei clase date.
Regresie liniara | Regresie logistică |
|---|---|
Regresia liniară este utilizată pentru a prezice variabila dependentă continuă folosind un set dat de variabile independente. | Regresia logistică este utilizată pentru a prezice variabila dependentă categorială folosind un set dat de variabile independente. |
Regresia liniară este utilizată pentru rezolvarea problemelor de regresie. | Este folosit pentru rezolvarea problemelor de clasificare. |
În aceasta se prezice valoarea variabilelor continue | În aceasta predicăm valorile variabilelor categorice |
În aceasta găsim linia cea mai potrivită. | În aceasta găsim S-Curve. |
Metoda de estimare a celor mai mici pătrate este utilizată pentru estimarea preciziei. | Metoda de estimare a probabilității maxime este utilizată pentru Estimarea acurateței. |
Ieșirea trebuie să fie o valoare continuă, cum ar fi prețul, vârsta etc. | Ieșirea trebuie să fie o valoare categorică, cum ar fi 0 sau 1, Da sau nu etc. |
A necesitat o relație liniară între variabilele dependente și independente. | Nu necesita o relație liniară. |
Poate exista coliniaritate între variabilele independente. | Nu ar trebui să existe coliniaritate între variabilele independente. |
Regresie logistică – Întrebări frecvente (FAQs)
Ce este regresia logistică în învățarea automată?
Regresia logistică este o metodă statistică pentru dezvoltarea modelelor de învățare automată cu variabile binare dependente, adică binare. Regresia logistică este o tehnică statistică utilizată pentru a descrie datele și relația dintre o variabilă dependentă și una sau mai multe variabile independente.
Care sunt cele trei tipuri de regresie logistică?
Regresia logistică este clasificată în trei tipuri: binară, multinomială și ordinală. Ele diferă atât ca execuție, cât și ca teorie. Regresia binară se referă la două rezultate posibile: da sau nu. Regresia logistică multinomială este utilizată atunci când există trei sau mai multe valori.
De ce este folosită regresia logistică pentru problema de clasificare?
Regresia logistică este mai ușor de implementat, interpretat și antrenat. Clasifică foarte rapid înregistrările necunoscute. Când setul de date este separabil liniar, funcționează bine. Coeficienții modelului pot fi interpretați ca indicatori ai importanței caracteristicilor.
Ce diferențiază regresia logistică de regresia liniară?
În timp ce regresia liniară este utilizată pentru a prezice rezultate continue, regresia logistică este folosită pentru a prezice probabilitatea ca o observație să se încadreze într-o anumită categorie. Regresia logistică folosește o funcție logistică în formă de S pentru a mapa valorile prezise între 0 și 1.
Logica de ordinul 1
Ce rol joacă funcția logistică în regresia logistică?
Regresia logistică se bazează pe funcția logistică pentru a converti rezultatul într-un scor de probabilitate. Acest scor reprezintă probabilitatea ca o observație să aparțină unei anumite clase. Curba în formă de S ajută la limitarea și clasificarea datelor în rezultate binare.
