Porți logice sunt componentele fundamentale ale tuturor circuitelor și sistemelor digitale. În electronica digitală, există șapte tipuri principale de porți logice folosit pentru a efectua diverse operații logice. O poartă logică este în esență un circuit electronic proiectat utilizând componente precum diode, tranzistori, rezistențe, condensatori , etc., și capabile să efectueze operații logice. În acest articol, vom studia definiția, tabelul de adevăr și alte concepte conexe ale porților logice. Deci, să începem cu introducerea de bază a porților logice.

Cuprins

• Ce este o poartă logică?
• Tipuri de porți logice
• SI Poarta
• SAU Poarta
• NU Poarta
• Poarta NOR
• Poarta NAND
• Poarta XOR
• Poarta XNOR
• Aplicații ale porților logice

Ce este o poartă logică?

A poarta logica este un circuit electronic proiectat utilizând componente electronice precum diode, tranzistori, rezistențe și multe altele. După cum sugerează și numele, o poartă logică este concepută pentru a efectua operații logice în sisteme digitale precum computere, sisteme de comunicații etc.

Prin urmare, putem spune că blocurile de bază ale unui circuit digital sunt porți logice, care execută numeroase operații logice care sunt cerute de orice circuit digital. O poartă logică poate lua două sau mai multe intrări, dar produce o singură ieșire. Ieșirea unei porți logice depinde de combinația de intrări și de operația logică pe care o efectuează.

Utilizarea porților logice algebră booleană pentru a executa procese logice. Porțile logice se găsesc în aproape fiecare gadget digital pe care îl folosim în mod regulat. Porțile logice sunt folosite în arhitectura telefoanelor, laptopurilor, tabletelor și dispozitivelor de memorie.

Tipuri de porți logice

O poartă logică este o poartă digitală care permite manipularea datelor. Porți logice, utilizați logica pentru a determina dacă să treceți sau nu un semnal. Porțile logice, pe de altă parte, guvernează fluxul de informații bazat pe un set de reguli.

Porțile logice pot fi clasificate în următoarele tipuri majore:

1. Porți logice de bază

Există trei porți logice de bază:

1. SI Poarta
2. SAU Poarta
3. NU Poarta

2. Porți logice universale

În electronica digitală, următoarele două porți logice sunt considerate porți logice universale:

1. Poarta NOR
2. Poarta NAND

3. Porți logice derivate

Următoarele două sunt porțile logice derivate utilizate în sistemele digitale:

1. Poarta XOR
2. Poarta XNOR

Să discutăm acum fiecare dintre aceste tipuri de porți logice în detaliu, una câte una.

SI Poarta

În electronica digitală, poarta AND este una dintre porțile logice de bază care realizează multiplicarea logică a intrărilor aplicate acesteia. Acesta generează o ieșire mare sau 1 logic, numai când toate intrările aplicate acesteia sunt ridicate sau 1 logic. În caz contrar, ieșirea porții AND este scăzută sau 0 logic.

Proprietăți ale porții AND:

Următoarele sunt două proprietăți principale ale porții AND:

• Poarta AND poate accepta două sau mai mult de două valori de intrare simultan.
• Când toate intrările sunt 1 logic, ieșirea acestei porți este 1 logic.

Funcționarea unei porți AND este descrisă de o expresie matematică, care se numește expresia booleană a porții AND.

Pentru poarta AND cu două intrări, expresia booleană este dată de,

Z = A.B

Unde, A și B sunt intrări la poarta AND, în timp ce Z denotă ieșirea porții AND.

Putem extinde această expresie la orice număr de variabile de intrare, cum ar fi,

şir.valoare a

Z=A.B.C.D…

Tabelul de adevăr al porții AND:

Tabelul de adevăr al unei porți AND cu două intrări este prezentat mai jos:

Simbolul porții AND:

Simbolul logic al unei porti SI cu doua intrari este prezentat in figura urmatoare.

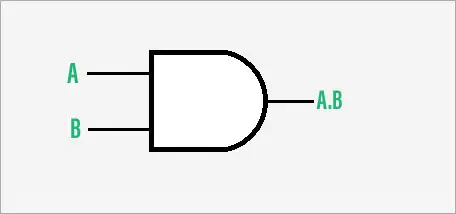
Simbol al porții AND cu două intrări

SAU Poarta

În electronica digitală, există un tip de poartă logică de bază care produce o ieșire scăzută sau 0 logic numai atunci când toate intrările sale sunt scăzute sau 0 logic. Pentru toate celelalte combinații de intrare, ieșirea porții SAU este ridicată sau 1 logic. poarta logică este denumită poartă SAU. O poartă SAU poate fi proiectată să aibă două sau mai multe intrări, dar o singură ieșire. Funcția principală a porții SAU este de a efectua operația de sumă logică.

Proprietățile porții OR:

O poartă SAU are următoarele două proprietăți:

• Poate avea două sau mai multe linii de intrare simultan.
• Când toate intrările la poarta SAU sunt scăzute sau 0 logic, ieșirea acesteia este scăzută sau 0 logic.

Funcționarea unei porți SAU poate fi descrisă matematic printr-o expresie matematică numită expresie booleană a porții SAU.

Expresia booleană pentru o poartă SAU cu două intrări este dată de,

Z = A + B

Expresia booleană pentru o poartă SAU cu trei intrări este,

Z = A + B + C

Aici, A, B și C sunt intrări și Z este variabilele de ieșire. Putem extinde această expresie booleană la orice număr de variabile de intrare.

Tabelul de adevăr al porții SAU:

Tabelul de adevăr al unei porți SAU descrie relația dintre intrări și ieșiri. Următorul este tabelul de adevăr pentru poarta SAU cu două intrări:

Simbolul porții OR:

Simbolul logic al unei porți SAU cu două intrări este prezentat în figura următoare.

Simbol al porții SAU cu două intrări

NU Poarta

În electronica digitală, poarta NOT este o altă poartă logică de bază folosită pentru a efectua complement al unui semnal de intrare aplicat acestuia. Este nevoie de o singură intrare și o singură ieșire. Ieșirea porții NOT este complementară a intrării aplicate acesteia. Prin urmare, dacă aplicăm o ieșire scăzută sau logică 0 porții NOT, se dă o ieșire ridicată sau logică 1 și invers. Poarta NOT este cunoscută și sub denumirea de invertor, deoarece efectuează operația de inversare.

Proprietățile porții NOT:

• Ieșirea unei porți NOT este complementară sau inversă a intrării aplicate acesteia.
• poarta NOT are doar o ieșire.

Funcționarea logică a porții NOT este descrisă de expresia sa booleană, care este dată mai jos.

Z= overline{A}

Bara de deasupra variabilei de intrare A reprezintă operația de inversare.

Tabelul de adevăr al porții SAU:

Tabelul de adevăr descrie relația dintre intrare și ieșire. Următorul este tabelul de adevăr pentru poarta NOT:

Simbol al porții NOT

Simbolul circuitului logic al unei porți NOT este prezentat în figura următoare. Aici, A este linia de intrare și Z este linia de ieșire.

jdbc

Simbol al NU Porții

Poarta NOR

Poarta NOR este un tip de poartă logică universală care poate lua două sau mai multe intrări, dar o ieșire. Este practic o combinație de două porți logice de bază, adică poarta SAU și poarta NOT. Astfel, poate fi exprimat astfel:

NOR Gate = OR Gate + NOT Gate

Cu alte cuvinte, o poartă NOR este o poartă SAU urmată de o poartă NOT.

Proprietățile porții NOR:

Următoarele sunt două proprietăți importante ale porții NOR:

• O poartă NOR poate avea două sau mai multe intrări și oferă o ieșire.
• O poartă NOR dă o ieșire mare sau 1 logic numai atunci când toate intrările sale sunt scăzute sau 0 logic.

Similar cu porțile logice de bază, putem descrie funcționarea unei porți NOR folosind o ecuație matematică numită expresie booleană a porții NOR.

Expresia booleană a unei porți NOR cu două intrări este dată mai jos:

C=overline{A+B}

Putem extinde această expresie la orice număr de variabile de intrare.

În expresiile booleene de mai sus, variabilele A și B sunt numite variabile de intrare, în timp ce variabila C este numită variabilă de ieșire.

Tabelul de adevăr al porții NOR:

Următorul este tabelul de adevăr al unei porți NOR cu două intrări care arată relația dintre intrările și ieșirile sale:

Simbol al Porții NOR

Poarta NAND

În electronica digitală, poarta NAND este un alt tip de poartă logică universală folosită pentru a efectua operații logice. Poarta NAND efectuează operația inversă a porții AND. Similar cu poarta NOR, poarta NAND poate avea, de asemenea, două sau mai multe linii de intrare, dar o singură linie de ieșire.

Poarta NAND este, de asemenea, reprezentată ca o combinație a două porți logice de bază și anume, poarta AND și poarta NOT. Prin urmare, poate fi exprimat ca

NAND Gate = AND Gate + NOT Gate

Proprietățile porții NAND:

Următoarele sunt cele două proprietăți cheie ale porții NAND:

• Poarta NAND poate prelua două sau mai multe intrări simultan și produce o ieșire pe baza combinației de intrări aplicate.
• Poarta NAND produce o ieșire scăzută sau 0 logic numai atunci când toate intrările sale sunt ridicate sau 1 logic.

Putem descrie expresia porții NAND printr-o ecuație matematică numită expresia sa booleană. Iată expresia booleană a unei porți NAND cu două intrări.

C=overline{AB}

În această expresie, A și B sunt variabilele de intrare și C este variabila de ieșire. Putem extinde această relație la orice număr de variabile de intrare, cum ar fi trei, patru sau mai multe.

Tabelul de adevăr al porții NAND:

Tabelul de adevăr este un tabel de intrări și ieșiri care descrie funcționarea porții NAND și arată relația logică dintre ele:

Simbolul porții NAND:

Simbolul logic al unei porți NAND este reprezentat ca o poartă AND cu un balon la capătul său de ieșire, așa cum este prezentat în figura următoare. Este simbolul unei porți NAND cu două intrări.

Simbol al porții NAND

Poarta XOR

În electronica digitală, există o poartă logică special concepută, numită poarta XOR, care este utilizată în circuitele digitale pentru a efectua modul de sumă . Este denumit și ca Poarta OR exclusivă sau poarta Ex-OR . Poarta XOR poate lua doar două intrări simultan și poate oferi o ieșire. Ieșirea porții XOR este mare sau 1 logic numai atunci când cele două intrări ale sale sunt diferite.

Proprietățile porții XOR:

Următoarele două sunt principalele proprietăți ale porții XOR:

• Poate accepta doar două intrări simultan. Nu există nimic ca o poartă XOR cu trei sau mai multe intrări.
• Ieșirea porții XOR este logic 1 sau mare, atunci când intrările sale sunt diferite.

Funcționarea porții XOR poate fi descrisă printr-o ecuație matematică numită expresia sa booleană. Următoarea este expresia booleană pentru ieșirea porții XOR.

Z=A oplus B

Aici, Z este variabila de ieșire, iar A și B sunt variabilele de intrare.

Această expresie poate fi scrisă și după cum urmează:

Z=A overline{B}+overline{A}B

Tabelul de adevăr al porții XOR:

Tabelul de adevăr este un tabel de intrări și ieșiri care descriu relația dintre acestea și funcționarea porții XOR pentru diferite combinații de intrări. Tabelul de adevăr al porții XOR este prezentat mai jos:

Simbolul porții XOR:

Simbolul logic al unei porți XOR este prezentat în figura următoare.

Simbol al porții XOR

Poarta XNOR

Poarta XNOR este un alt tip de poartă logică cu scop special folosit pentru implementare operare exclusivă în circuite digitale . Este folosit pentru implementarea operațiunii NOR exclusiv în circuite digitale. Se mai numește și poarta Ex-NOR sau Exclusive NOR. Este o combinație de două porți logice și anume, poarta XOR și poarta NOT. Astfel, poate fi exprimat astfel:

Linux rulează cmd

Poarta XNOR = Poarta XOR + Poarta NOT

Ieșirea unei porți XNOR este mare sau 1 logic atunci când ambele intrări sunt similare. În caz contrar, ieșirea este scăzută sau 0 logic. Prin urmare, poarta XNOR este folosită ca circuit detector de similaritate.

Proprietățile porții XNOR:

Următoarele sunt două proprietăți cheie ale porții XNOR:

• Poarta XNOR ia doar două intrări și produce o ieșire.
• Ieșirea porții XNOR este ridicată sau 1 logic numai atunci când are intrări similare.

Funcționarea porții XNOR poate fi descrisă printr-o ecuație matematică numită expresia booleană a porții XNOR. Iată expresia booleană a porții XNOR.

Y=A odot B

De asemenea, putem scrie această expresie după cum urmează:

Y=AB + overline{A} overline{B}

Aici, A și B sunt intrări și Y este ieșirea.

Tabelul de adevăr al porții XNOR:

Tabelul de adevăr al porții XNOR este prezentat mai jos. Acest tabel de adevăr descrie relația dintre intrările și ieșirile porții XNOR.

Simbolul porții XNOR:

Simbolul logic al porții XNOR este prezentat în figura următoare. Aici, A și B sunt intrări și Y este ieșirea.

Simbol al porții XNOR

Aplicații ale porților logice

Porțile logice sunt elementele fundamentale ale tuturor circuitelor și dispozitivelor digitale precum computerele. Iată câteva dispozitive digitale cheie în care sunt utilizate porți logice pentru a-și proiecta circuitele:

• Calculatoare
• Microprocesoare
• Microcontrolere
• Ceasuri digitale și inteligente
• Smartphone-uri etc.

Bazat pe Porți Logice – Întrebări frecvente

Ce sunt porțile logice?

Porțile logice sunt circuite digitale care efectuează operații logice pe intrarea care le este furnizată și produc o ieșire corespunzătoare.

Ce sunt porțile universale?

Pentru a realiza un proces logic specific, porțile universale sunt create prin îmbinarea a două sau mai multe porți fundamentale. Porțile universale sunt porți NAND și NOR.

Care este ieșirea unei porți NOT când se aplică intrarea 0?

Pentru că NOT gate este un invertor. Ca rezultat, dacă 0 este folosit ca intrare, ieșirea va fi 1.

Care poartă logică este cunoscută sub numele de invertor?

Un invertor este cunoscut și sub numele de poartă NOT. Ieșirea obținută este inversul intrării.

Care este expresia booleană pentru poarta SAU?

Dacă A și B sunt intrarea, atunci ieșirea porții SAU poate fi dată ca Y=A+B.

Care este expresia booleană pentru poarta XNOR?

Dacă A și B sunt intrarea, atunci ieșirea porții XNOR poate fi dată ca Y=A.B+A’B’.