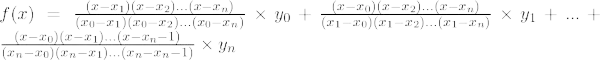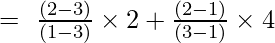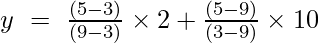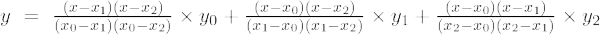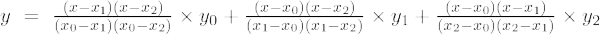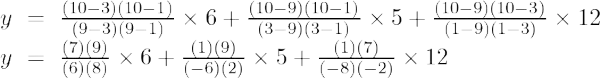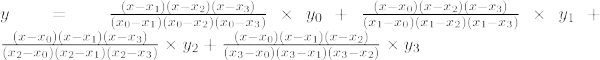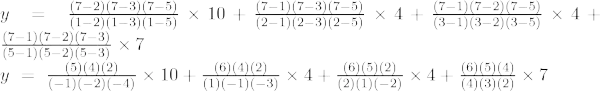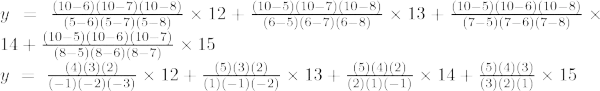logo

TechCodeview

Formula de interpolare Lagrange

Formula de interpolare Lagrange găsește un polinom numit polinom Lagrange care ia anumite valori într-un punct arbitrar. Este un grad al n-lea expresia polinomială a funcției f(x). Metoda de interpolare este utilizată pentru a găsi noile puncte de date în intervalul unui set discret de puncte de date cunoscute.

În acest articol, vom afla despre, Interpolarea Lagrange, Formula de interpolare Lagrange, Dovada pentru Formula de interpolare Lagrange, Exemple bazate pe Formula de interpolare Lagrange și altele în detaliu.



Ce este interpolarea Lagrange?

Interpolarea Lagrange este o modalitate de a găsi valoarea oricărei funcții în orice punct dat atunci când funcția nu este dată. Folosim alte puncte ale funcției pentru a obține valoarea funcției în orice punct necesar.

Să presupunem că avem o funcție y = f(x) în care înlocuirea valorilor lui x dă diferite valori ale lui y. Și ni se dau două puncte (x1, și1) și (x2, și2) pe curbă, atunci valoarea lui y la x = a(constant) este calculată utilizând Formula de interpolare Lagrange.

Formula de interpolare Lagrange

Având în vedere câteva valori reale x1, X2, X3, …, Xnși y1, și2, și3, …, șinși va exista un polinom P cu coeficienți reali care îndeplinesc condițiile P(xi) = șii, ∀ i = {1, 2, 3, …, n} și gradul polinomului P trebuie să fie mai mic decât numărul valorilor reale, adică gradul(P)



Formula de interpolare Lagrange pentru ordinul al n-lea

Formula de interpolare Lagrange pentru nthpolinomul de grade este dat mai jos:

Formula de interpolare Lagrange pentru n th ordinea este,

f(x)=frac{(x-x_1)(x-x_2)...(x-x_n)}{(x_0-x_1)(x_0-x_2)...(x_0-x_n)} imes y_0+ frac{(x-x_0)(x-x_2)...(x-x_n)}{(x_1-x_0)(x_1-x_2)...(x_1-x_n)} imes y_1+...+ frac{(x-x_0)(x-x_1)...(x-x_n-1)}{(x_n-x_0)(x_n-x_1)...(x_n-x_n-1)} imes y_n



Formula de interpolare de ordinul întâi Lagrange

Dacă Gradul polinomului este 1, atunci se numește polinom de ordinul întâi. Formula de interpolare Lagrange pentru 1Sfpolinoamele de ordine este,

f(x)~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

Formula de interpolare de ordinul doi Lagrange

Dacă gradul polinomului este 2, atunci se numește polinom de ordinul doi. Formula de interpolare Lagrange pentru polinoamele de ordinul 2 este,

f(x)~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)} {(x_1-x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2

Demonstrarea teoremei Lagrange

Să considerăm un polinom de gradul n al formei date,

f(x) = A0(x – x1)(x – x2)(x – x3)…(x – xn) + A1(x – x1)(x – x2)(x – x3)…(x – xn) + … + A(n-1)(x – x1)(x – x2)(x – x3)…(x – xn)

Înlocuiți observațiile xia primi oi

Pune x = x0atunci obținem A0

f(x0) = și0= A0(X0- X1)(X0- X2)(X0- X3)…(X0- Xn)

A 0 = și 0 /(X 0 - X 1 )(X 0 - X 2 )(X 0 - X 3 )…(X 0 - X n )

Prin substituirea x = x1primim A1

f(x1) = și1= A1(X1- X0)(X1- X2)(X1- X3)…(X1- Xn)

A 1 = și 1 /(X 1 - X 0 )(X 1 - X 2 )(X 1 - X 3 )…(X 1 - X n )

În mod similar, înlocuind x = xnprimim An

f(xn) = șin= An(Xn- X0)(Xn- X1)(Xn- X2)…(Xn- Xn-1)

A n = și n /(X n - X 0 )(X n - X 1 )(X n - X 2 )…(X n - X n-1 )

Dacă înlocuim toate valorile lui Aiîn funcția f(x) unde i = 1, 2, 3, …n atunci obținem Formula de interpolare Lagrange ca,

converti char în șir

f(x)~=~frac{(x-x_1)(x-x_2)...(x-x_n)}{(x_0-x_1)(x_0-x_2)...(x_0-x_n)} ori y_0+frac{(x-x_0)(x-x_2)...(x-x_n)}{(x_1-x_0)(x_1-x_2)...(x_1-x_n)} imes y_1+... +frac{(x-x_0)(x-x_1)...(x-x_n-1)}{(x_n-x_0)(x_n-x_1)...(x_n-x_n-1)} imes y_n

Proprietățile formulei de interpolare Lagrange

Diferite proprietăți ale formulei de interpolare Lagrange sunt discutate mai jos,

  • Această formulă este folosită pentru a găsi valoarea funcției în orice moment, chiar și atunci când funcția în sine nu este dată.
  • Se folosește chiar dacă punctele date nu sunt distanțate uniform.
  • Oferă valoarea variabilei dependente pentru orice variabilă independentă aparținând oricărei funcții și, prin urmare, este utilizată în Analiza numerică pentru găsirea valorilor funcției etc.

Utilizări ale formulei de interpolare Lagrange

Diverse utilizări ale formulei de interpolare Lagrange sunt discutate mai jos,

  • Este folosit pentru a găsi valoarea variabilei dependente la orice variabilă independentă anume, chiar dacă funcția în sine nu este dată.
  • Este folosit la scalarea imaginilor.
  • Este folosit în modelarea AI.
  • Este folosit pentru a preda NLP-urile etc.

Citeşte mai mult,

  • Formula de interpolare
  • Formula de interpolare liniară

Exemple de utilizare a formulei de interpolare Lagrange

Să analizăm câteva exemple de întrebări despre Formula de interpolare Lagrange.

Exemplul 1: Găsiți valoarea lui y la x = 2 pentru setul dat de puncte (1, 2), (3, 4)

Soluţie:

Dat,

  • (X0, și0) = (1, 2)
  • (X1, și1) = (3, 4)

Formula de interpolare Lagrange de ordinul întâi este,

y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

La x = 2

și =~frac{(2-3)}{(1-3)} imes 2+frac{(2-1)}{(3-1)} imes 4

y = (-2/-2) + (4/2)

y = 1 + 2 = 3

Valoarea lui y la x = 2 este 3

Exemplul 2: Găsiți valoarea lui y la x = 5 pentru setul dat de puncte (9, 2), (3, 10)

Soluţie:

Dat,

  • (X0, și0) = (9, 2)
  • (X1, și1) = (3, 10)

Formula de interpolare Lagrange de ordinul întâi este,

y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

La x = 5

y~=~frac{(5-3)}{(9-3)} imes 2+frac{(5-9)}{(3-9)} imes 10

y = (4/6) + (-40/-6)

y = (2/3) + (20/3)

y = 22/3 = 7,33

Valoarea lui y la x = 5 este 7,33

Citirea fișierului csv în java

Exemplul 3: Găsiți valoarea lui y la x = 1 pentru setul dat de puncte (1, 6), (3, 4), (2, 5)

Soluţie:

Dat,

  • (X0, și0) = (1, 6)
  • (X1, și1) = (3, 4)
  • (X2, și2) = (2, 5)

Formula de interpolare Lagrange de ordinul doi este,

y~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)}{(x_1 -x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2

La x = 1

y~=~frac{(1-3)(1-2)}{(1-3)(1-2)} ime 6+frac{(1-1)(1-2)}{( 3-1)(3-2)}ori 4+frac{(1-1)(1-3)}{(2-1)(2-3)}ori 5 y~=~ frac{(-2)(-1)}{(-2)(-1)} imes 6+frac{(0)(-1)}{(2)(1)} imes 4+frac {(0)(-2)}{(1)(-1)}ori 5

y = (12/2) + 0 + 0

y = 6

Valoarea lui y la x = 1 este 6

Exemplul 4: Găsiți valoarea lui y la x = 10 pentru setul dat de puncte (9, 6), (3, 5), (1, 12)

Soluţie:

Dat,

  • (X0, și0) = (9, 6)
  • (X1, și1) = (3, 5)
  • (X2, și2) = (1, 12)

Formula de interpolare Lagrange de ordinul doi este,

y~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)}{(x_1 -x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2

La x = 10

y~=~frac{(10-3)(10-1)}{(9-3)(9-1)} imes 6+frac{(10-9)(10-1)}{( 3-9)(3-1)} imes 5+frac{(10-9)(10-3)}{(1-9)(1-3)} imes 12 y~=~ frac{(7)(9)}{(6)(8)} ime 6+frac{(1)(9)}{(-6)(2)} ime 5+frac{(1) (7)}{(-8)(-2)}ori 12

mit forma completa

y = (63/8) + (-15/4) + (21/4)

y = (63-30 + 42)/8

y = 75/8 = 9,375

Valoarea lui y la x = 10 este 9,375

Exemplul 5: Găsiți valoarea lui y la x = 7 pentru setul dat de puncte (1, 10), (2, 4), (3, 4), (5, 7)

Soluţie:

Dat,

  • (X0, și0) = (1, 10)
  • (X1, și1) = (2, 4)
  • (X2, și2) = (3, 4)
  • (X3, și3) = (5, 7)

Formula de interpolare Lagrange de ordinul trei este,

y~=~frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)} imes y_0+frac{(x-x_0 )(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)} imes y_1+frac{(x-x_0)(x-x_1)(x-x_3) }{(x_2-x_0)(x_2-x_1)(x_2-x_3)} imes y_2+frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1 )(x_3-x_2)} imes y_3

La x = 7

y~=~frac{(7-2)(7-3)(7-5)}{(1-2)(1-3)(1-5)} ime 10+frac{(7- 1)(7-3)(7-5)}{(2-1)(2-3)(2-5)}ori 4+frac{(7-1)(7-2)(7- 5)}{(3-1)(3-2)(3-5)} ime 4+frac{(7-1)(7-2)(7-3)}{(5-1)( 5-2)(5-3)} imes 7 y~=~frac{(5)(4)(2)}{(-1)(-2)(-4)} imes 10+ frac{(6)(4)(2)}{(1)(-1)(-3)} ime 4+frac{(6)(5)(2)}{(2)(1) (-2)} imes 4+frac{(6)(5)(4)}{(4)(3)(2)} imes 7

y = -50 + 64 – 60 + 35

y = 99 – 110 = -unsprezece

Valoarea lui y la x = 7 este -11

Exemplul 6: Găsiți valoarea lui y la x = 10 pentru setul dat de puncte (5, 12), (6, 13), (7, 14), (8, 15)

concatenare de șiruri

Soluţie:

Dat,

  • (X0, și0) = (5, 12)
  • (X1, și1) = (6, 13)
  • (X2, și2) = (7, 14)
  • (X3, și3) = (8, 15)

Formula de interpolare Lagrange de ordinul trei este,

y~=~frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)} imes y_0+frac{(x-x_0 )(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)} imes y_1+frac{(x-x_0)(x-x_1)(x-x_3) }{(x_2-x_0)(x_2-x_1)(x_2-x_3)} imes y_2+frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1 )(x_3-x_2)} imes y_3

La x = 10,

y~=~frac{(10-6)(10-7)(10-8)}{(5-6)(5-7)(5-8)} imes 12+frac{(10- 5)(10-7)(10-8)}{(6-5)(6-7)(6-8)}ori 13+frac{(10-5)(10-6)(10- 8)}{(7-5)(7-6)(7-8)} ime 14+frac{(10-5)(10-6)(10-7)}{(8-5)( 8-6)(8-7)} imes 15 y~=~frac{(4)(3)(2)}{(-1)(-2)(-3)} imes 12+ frac{(5)(3)(2)}{(1)(-1)(-2)} ime 13+frac{(5)(4)(2)}{(2)(1) (-1)} imes 14+frac{(5)(4)(3)}{(3)(2)(1)} imes 15

y = -48 + 195 – 280 + 150

y = 17

Valoarea lui y la x = 10 este 17

Exemplul 7: Găsiți valoarea lui y la x = 0 pentru setul dat de puncte (-2, 5),(1, 7)

Soluţie:

Dat,

  • (X0, și0) = (-2, 5)
  • (X1, și1) = (1, 7)

Formula de interpolare Lagrange de ordinul întâi este,

y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

La x = 0,

y~=~frac{(0-1)}{(-2-1)} imes 5+frac{(0+2)}{(1+2)} imes 7

y = (5/3) + (14/3)

y = 19/3 = 6,33

Valoarea lui y la x = 0 este 6,33

Întrebări frecvente despre Formula de interpolare Lagrange

1. Ce este Formula de interpolare Lagrange?

Formula de interpolare Lagrange este o formulă care este utilizată pentru a găsi valoarea variabilei dependente a funcției pentru orice variabilă independentă, chiar dacă funcția în sine nu este dată.

2. Care sunt aplicațiile formulei de interpolare Lagrange?

Formula Lagranges are diverse aplicații în matematica modernă și științele datelor,

  • Este folosit pentru a modela AI Traning.
  • Este folosit în procesarea imaginilor.
  • Este folosit în reprezentarea grafică a curbelor 3D și mai mari etc.

3. Ce este formula de interpolare Lagrange de ordinul întâi?

Formula de interpolare Lagranges de ordinul întâi este,

f(x) = (x – x 1 )/(X 0 - X 1 )×f 0 + (x – x 0 )/(X 1 - X 0 )×f 1

4. Ce este formula de interpolare Lagrange de ordinul doi?

Formula de interpolare Lagranges de ordinul doi este,

f(x) = [(x – x 1 )(x – x 2 )/(X 0 - X 1 )(X 0 - X 2 )]×f 0 + [(x – x 0 )(x – x 2 )/(X 1 - X 0 )(X 1 - X 2 )]×f 1 + [(x – x 0 )(x – x 1 )/(X 2 - X 0 )(X 2 - X 2 )]×f 0