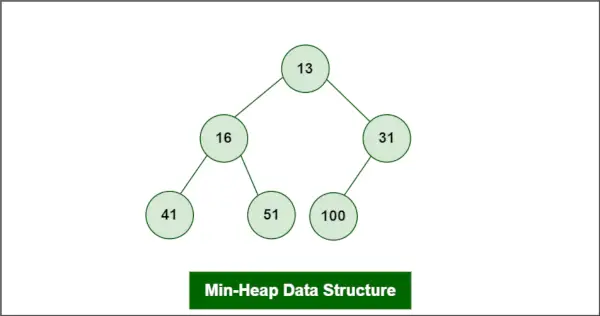
A Min-Heap este definit ca un tip de Structura de date heap este un tip de arbore binar care este utilizat în mod obișnuit în informatică în diverse scopuri, inclusiv sortarea, căutarea și organizarea datelor.
Introducere în Min-Heap – Tutoriale privind structura datelor și algoritmi
Scopul și cazurile de utilizare ale min-heap:
- Implementarea Cozii prioritare: Una dintre utilizările principale ale structurii de date heap este pentru implementarea cozilor prioritare.
- Algoritmul lui Dijkstra : Algoritmul lui Dijkstra este un algoritm de calea cea mai scurtă care găsește calea cea mai scurtă între două noduri dintr-un grafic. Un min heap poate fi folosit pentru a ține evidența nodurilor nevizitate cu cea mai mică distanță față de nodul sursă.
- Triere: Un min heap poate fi folosit ca algoritm de sortare pentru a sorta eficient o colecție de elemente în ordine crescătoare.
- Constatare mediană: Un heap min poate fi folosit pentru a găsi eficient mediana unui flux de numere. Putem folosi o grămadă min pentru a stoca jumătatea mai mare a numerelor și o grămadă maximă pentru a stoca jumătatea mai mică. Mediana va fi rădăcina grămezii min.
Structura de date Min-Heap în diferite limbi:
1. Min-Heap în C++
Un min heap poate fi implementat folosind priority_queue container din Biblioteca de șabloane standard (STL). The priority_queue container este un tip de adaptor de container care oferă o modalitate de a stoca elemente într-o structură de date asemănătoare coadă, în care fiecare element are o prioritate asociată.
Sintaxă :
C++ priority_queue < int, vector , mai mare > minH;>>> 2. Min-Heap în Java
În Java, un heap min poate fi implementat folosind PriorityQueue clasa de la pachetul java.util . Clasa PriorityQueue este o coadă de prioritate care oferă o modalitate de a stoca elemente într-o structură de date asemănătoare coadă, în care fiecare element are o prioritate asociată.
Sintaxă :
JavaMin-Heap în Python În Python, un heap min poate fi implementat folosind heapq modul, care oferă funcții pentru implementarea heap-urilor. Mai exact, cel heapq modulul oferă o modalitate de a crea și de a manipula structuri de date heap.
Sintaxă:
PitonÎn C#, un heap min poate fi implementat folosind clasa PriorityQueue din Sistem.Colecții.Spațiu de nume generic . Clasa PriorityQueue este o coadă de prioritate care oferă o modalitate de a stoca elemente într-o structură de date asemănătoare coadă, în care fiecare element are o prioritate asociată. Sintaxă:
C# var minHeap = new PriorityQueue ();>>>
5. Min-heap în JavaScript
Un min heap este un arbore binar în care fiecare nod are o valoare mai mică sau egală cu copiii săi. În JavaScript, puteți implementa un heap min folosind o matrice, unde primul element reprezintă nodul rădăcină și copiii unui nod la index i sunt situate la indici 2i+1 și 2i+2.
Sintaxă:
JavaScript Diferența dintre Min Heap și Max Heap:
Min Heap
Max Heap
1.
Într-un Min-Heap, cheia prezentă la nodul rădăcină trebuie să fie mai mică sau egală cu cheile prezente la toți copiii săi.
Într-un Max-Heap, cheia prezentă la nodul rădăcină trebuie să fie mai mare sau egală cu cheile prezente la toți copiii săi.
2.
Într-un Min-Heap elementul cheie minim este prezent la rădăcină.
Într-un Max-Heap, elementul cheie maxim este prezent la rădăcină.
3.
Un Min-Heap folosește prioritatea ascendentă.
Un Max-Heap folosește prioritatea descendentă.
4.
În construcția unui Min-Heap, cel mai mic element are prioritate.
În construcția unui Max-Heap, cel mai mare element are prioritate.
5.
Într-un Min-Heap, cel mai mic element este primul care este scos din grămada.
Într-un Max-Heap, cel mai mare element este primul care este scos din heap.
Implementarea internă a structurii de date Min-Heap:
A Heap-ul min este de obicei reprezentat ca o matrice .
- Elementul rădăcină va fi la Arr[0] .
- Pentru orice nod i Arr[i] :
- Arr[(i -1) / 2] returnează nodul său părinte.
- Arr[(2 * i) + 1] returnează nodul său copil stâng.
- Arr[(2 * i) + 2] returnează nodul său copil drept.
Implementarea internă a Min-Heap necesită 3 pași majori:
- Inserare : Pentru a insera un element în heap-ul min, mai întâi adăugăm elementul la sfârșitul matricei și apoi ajustăm proprietatea heap schimbând în mod repetat elementul cu părintele său, până când acesta este în poziția corectă.
- Ștergere : Pentru a elimina elementul minim din heap-ul min, mai întâi schimbăm nodul rădăcină cu ultimul element din matrice, eliminăm ultimul element și apoi ajustăm proprietatea heap schimbând în mod repetat elementul cu cel mai mic element al său, până când acesta se află în pozitia corecta.
- Heapify : O operație heapify poate fi folosită pentru a crea un min heap dintr-o matrice nesortată.
Operațiuni pe structura de date min-heap și implementarea lor:
Iată câteva operațiuni comune care pot fi efectuate pe o structură de date Heap,
1. Inserarea în Structura de date Min-Heap :
Elementele pot fi inserate în heap urmând o abordare similară cu cea discutată mai sus pentru ștergere. Ideea este de a:
- Operația de inserare într-un min-heap implică următorii pași:
- Adăugați noul element la sfârșitul heap-ului, în următoarea poziție disponibilă din ultimul nivel al arborelui.
- Comparați noul element cu părintele său. Dacă părintele este mai mare decât noul element, schimbați-le.
- Repetați pasul 2 până când părintele este mai mic sau egal cu noul element, sau până când noul element ajunge la rădăcina arborelui.
- Noul element este acum în poziția corectă în heap-ul min, iar proprietatea heap este satisfăcută.
Ilustrare:
Să presupunem că Heap-ul este un Min-Heap ca:
Inserarea în Min-Heap
Implementarea operațiunii de inserare în min-heap:
C++ #include #include using namespace std; // Function to insert a new element into the min-heap void insert_min_heap(vector & heap, int value) { // Adăugați noul element la sfârșitul heapului heap.push_back(valoare); // Obține indexul ultimului element int index = heap.size() - 1; // Comparați noul element cu părintele său și schimbați dacă // este necesar în timp ce (index> 0 && heap[(index - 1) / 2]> heap[index]) { swap(heap[index], heap[(index - 1) / 2]); // Mută în sus în arbore la părintele elementului curent // index = (index - 1) / 2; } } // Funcția principală pentru a testa funcția insert_min_heap int main() { vector morman; int valori[] = { 10, 7, 11, 5, 4, 13 }; int n = dimensiunea(valorilor) / dimensiunea(valorilor[0]); pentru (int i = 0; i< n; i++) { insert_min_heap(heap, values[i]); cout << 'Inserted ' << values[i] << ' into the min-heap: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; } return 0; }>
Java import java.util.*; public class GFG { // Function to insert a new element into the min-heap public static void insertMinHeap(int[] heap, int size, int value) { // Add the new element to the end of the heap heap[size] = value; // Get the index of the last element int index = size; // Compare the new element with its parent and swap // if necessary while (index>0 && heap[(index - 1) / 2]> heap[index]) { swap(heap, index, (index - 1) / 2); // Mută în sus în arbore la părintele elementului curent // index = (index - 1) / 2; } } // Funcție pentru a schimba două elemente într-un tablou public static void swap(int[] arr, int i, int j) { int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } // Funcția principală pentru a testa funcția insertMinHeap public static void main(String[] args) { int[] heap = new int[6]; int[] valori = { 10, 7, 11, 5, 4, 13 }; int dimensiune = 0; pentru (int i = 0; i< values.length; i++) { insertMinHeap(heap, size, values[i]); size++; System.out.print('Inserted ' + values[i] + ' into the min-heap: '); for (int j = 0; j < size; j++) { System.out.print(heap[j] + ' '); } System.out.println(); } } }> Python3 def insert_min_heap(heap, value): # Add the new element to the end of the heap heap.append(value) # Get the index of the last element index = len(heap) - 1 # Compare the new element with its parent and swap if necessary while index>0 și heap[(index - 1) // 2]> heap[index]: heap[index], heap[(index - 1) // 2] = heap[(index - 1) // 2], heap[ index] # Mută în sus în arbore la părintele elementului curent index = (index - 1) // 2 heap = [] valori = [10, 7, 11, 5, 4, 13] pentru valoarea în valori: insert_min_heap( heap, value) print(f'Inserat {valoare} în min-heap: {heap}')> C# using System; using System.Collections.Generic; public class Program { // Function to insert a new element into the min-heap static void InsertMinHeap(List heap, int value) { // Adăugați noul element la sfârșitul heapului heap.Add(valoare); // Obține indexul ultimului element int index = heap.Count - 1; // Comparați noul element cu părintele său și schimbați // dacă este necesar while (index> 0 && heap[(index - 1) / 2]> heap[index]) { int temp = heap[index]; heap[index] = heap[(index - 1) / 2]; heap[(index - 1) / 2] = temp; // Mută în sus în arbore la părintele elementului curent // index = (index - 1) / 2; } } // Funcția principală pentru a testa funcția InsertMinHeap public static void Main() { Listă heap = listă nouă (); int[] valori = { 10, 7, 11, 5, 4, 13 }; foreach(int value in values) { InsertMinHeap(heap, value); Consola.Scrie('Inserat ' + valoare + ' în heap-ul min: '); foreach(int element în heap) { Console.Write(element + ' '); } Console.WriteLine(); } } }>>> JavascriptInserted 10 into the min-heap: 10 Inserted 7 into the min-heap: 7 10 Inserted 11 into the min-heap: 7 10 11 Inserted 5 into the min-heap: 5 7 11 10 Inserted 4 into the min-heap: 4 5 11 10 7 Inser...>
Complexitatea timpului: O(log(n)) ( unde n este numărul de elemente din heap )
Spațiu auxiliar: Pe)
2. Ștergerea în Structura de date Min-Heap :
Eliminarea celui mai mic element (rădăcina) din grămada min. Rădăcina este înlocuită cu ultimul element din heap, iar apoi proprietatea heap este restaurată prin schimbarea noii rădăcini cu cel mai mic copil, până când părintele este mai mic decât ambii copii sau până când noua rădăcină ajunge la un nod frunză.
- Înlocuiți rădăcina sau elementul de șters cu ultimul element.
- Ștergeți ultimul element din Heap.
- Deoarece ultimul element este acum plasat în poziția nodului rădăcină. Deci, este posibil să nu urmeze proprietatea heap. Prin urmare, înghesuiți ultimul nod plasat la poziția rădăcinii.
Ilustrare :
Să presupunem că Heap-ul este un Min-Heap ca:
Structura de date Min-Heap
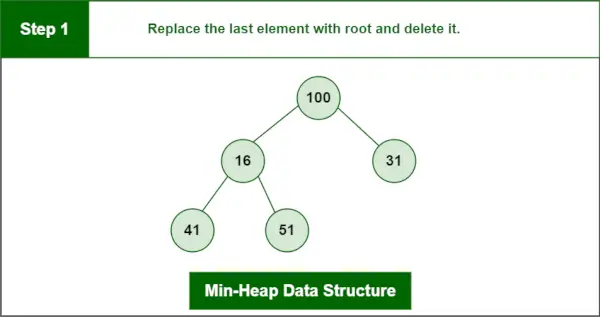
Elementul de șters este root, adică 13.
Proces :
Ultimul element este 100.
material unghiularPasul 1: Înlocuiți ultimul element cu root și ștergeți-l.
Structura de date Min-Heap
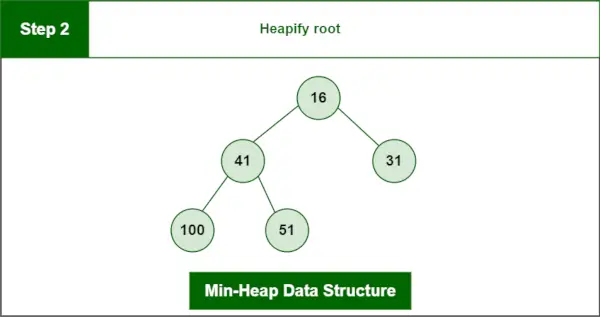
Pasul 2 : Heapify rădăcină.
Heap final:
Structura de date Min-Heap
Implementarea operațiunii de ștergere în Min-Heap:
C++ #include #include using namespace std; // Function to insert a new element into the min-heap void insert_min_heap(vector & heap, int value) { // Adăugați noul element la sfârșitul heapului heap.push_back(valoare); // Obține indexul ultimului element int index = heap.size() - 1; // Comparați noul element cu părintele său și schimbați dacă // este necesar în timp ce (index> 0 && heap[(index - 1) / 2]> heap[index]) { swap(heap[index], heap[(index - 1) / 2]); // Mută în sus în arbore la părintele elementului curent // index = (index - 1) / 2; } } // Funcție de ștergere a unui nod din min-heap void delete_min_heap(vector & heap, int value) { // Găsiți indexul elementului de șters int index = -1; pentru (int i = 0; i< heap.size(); i++) { if (heap[i] == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last // element heap[index] = heap[heap.size() - 1]; // Remove the last element heap.pop_back(); // Heapify the tree starting from the element at the // deleted index while (true) { int left_child = 2 * index + 1; int right_child = 2 * index + 2; int smallest = index; if (left_child < heap.size() && heap[left_child] < heap[smallest]) { smallest = left_child; } if (right_child < heap.size() && heap[right_child] < heap[smallest]) { smallest = right_child; } if (smallest != index) { swap(heap[index], heap[smallest]); index = smallest; } else { break; } } } // Main function to test the insert_min_heap and // delete_min_heap functions int main() { vector morman; int valori[] = { 13, 16, 31, 41, 51, 100 }; int n = dimensiunea(valorilor) / dimensiunea(valorilor[0]); pentru (int i = 0; i< n; i++) { insert_min_heap(heap, values[i]); } cout << 'Initial heap: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; delete_min_heap(heap, 13); cout << 'Heap after deleting 13: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; return 0; }>
Java import java.util.*; public class GFG { // Function to insert a new element into the min-heap public static void insertMinHeap(List heap, int value) { // Adăugați noul element la sfârșitul heapului heap.add(valoare); // Obține indexul ultimului element int index = heap.size() - 1; // Comparați noul element cu părintele său și schimbați // dacă este necesar în timp ce (index> 0 && heap.get((index - 1) / 2)> heap.get(index)) { Collections.swap(heap, index, (indice - 1) / 2); // Mută în sus în arbore la părintele elementului curent // index = (index - 1) / 2; } } // Funcție de ștergere a unui nod din min-heap public static void deleteMinHeap(List heap, int value) { // Găsiți indexul elementului de șters int index = -1; pentru (int i = 0; i< heap.size(); i++) { if (heap.get(i) == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last // element heap.set(index, heap.get(heap.size() - 1)); // Remove the last element heap.remove(heap.size() - 1); // Heapify the tree starting from the element at the // deleted index while (true) { int leftChild = 2 * index + 1; int rightChild = 2 * index + 2; int smallest = index; if (leftChild < heap.size() && heap.get(leftChild) < heap.get(smallest)) { smallest = leftChild; } if (rightChild < heap.size() && heap.get(rightChild) < heap.get(smallest)) { smallest = rightChild; } if (smallest != index) { Collections.swap(heap, index, smallest); index = smallest; } else { break; } } } // Main function to test the insertMinHeap and // deleteMinHeap functions public static void main(String[] args) { List heap = noua ArrayList (); int[] valori = { 13, 16, 31, 41, 51, 100 }; int n = valori.lungime; pentru (int i = 0; i< n; i++) { insertMinHeap(heap, values[i]); } System.out.print('Initial heap: '); for (int j = 0; j < heap.size(); j++) { System.out.print(heap.get(j) + ' '); } System.out.println(); deleteMinHeap(heap, 13); System.out.print('Heap after deleting 13: '); for (int j = 0; j < heap.size(); j++) { System.out.print(heap.get(j) + ' '); } System.out.println(); } }> Python3 def insert_min_heap(heap, value): heap.append(value) index = len(heap) - 1 while index>0 și heap[(index - 1) // 2]> heap[index]: heap[index], heap[(index - 1) // 2] = heap[(index - 1) // 2], heap[ index] index = (index - 1) // 2 def delete_min_heap(heap, value): index = -1 for i in range(len(heap)): if heap[i] == valoare: index = i break if index == -1: returnează heap[index] = heap[-1] heap.pop() în timp ce True: left_child = 2 * index + 1 right_child = 2 * index + 2 smallest = index dacă left_child< len(heap) and heap[left_child] < heap[smallest]: smallest = left_child if right_child < len(heap) and heap[right_child] < heap[smallest]: smallest = right_child if smallest != index: heap[index], heap[smallest] = heap[smallest], heap[index] index = smallest else: break heap = [] values = [13, 16, 31, 41, 51, 100] for value in values: insert_min_heap(heap, value) print('Initial heap:', heap) delete_min_heap(heap, 13) print('Heap after deleting 13:', heap)> C# using System; using System.Collections.Generic; class MinHeap { private List heap = listă nouă (); public void Insert(int value) { heap.Add(valoare); int index = heap.Număr - 1; while (index> 0 && heap[(index - 1) / 2]> heap[index]) { Swap(index, (index - 1) / 2); indice = (indice - 1) / 2; } } public void Delete(int value) { int index = heap.IndexOf(valoare); if (index == -1) { return; } heap[index] = heap[heap.Count - 1]; heap.RemoveAt(heap.Count - 1); while (adevărat) { int leftChild = 2 * index + 1; int rightChild = 2 * index + 2; int mai mic = index; dacă (leftChild< heap.Count && heap[leftChild] < heap[smallest]) { smallest = leftChild; } if (rightChild < heap.Count && heap[rightChild] < heap[smallest]) { smallest = rightChild; } if (smallest != index) { Swap(index, smallest); index = smallest; } else { break; } } } private void Swap(int i, int j) { int temp = heap[i]; heap[i] = heap[j]; heap[j] = temp; } public void Print() { for (int i = 0; i < heap.Count; i++) { Console.Write(heap[i] + ' '); } Console.WriteLine(); } } class Program { static void Main(string[] args) { MinHeap heap = new MinHeap(); int[] values = { 13, 16, 31, 41, 51, 100 }; for (int i = 0; i < values.Length; i++) { heap.Insert(values[i]); } Console.Write('Initial heap: '); heap.Print(); heap.Delete(13); Console.Write('Heap after deleting 13: '); heap.Print(); } }> Javascript function insertMinHeap(heap, value) { // Add the new element to the end of the heap heap.push(value); // Get the index of the last element let index = heap.length - 1; // Compare the new element with its parent and swap if necessary for (let flr = Math.floor((index - 1) / 2); index>0 && heap[flr]> heap[index]; flr = Math.floor((index - 1) / 2)) { [heap[index], heap[flr]] = [ heap[flr], heap[index], ]; // Mută în sus în arbore la părintele elementului curent index = Math.floor((index - 1) / 2); } } function deleteMinHeap(heap, value) { // Găsiți indexul elementului de șters let index = -1; pentru (fie i = 0; i< heap.length; i++) { if (heap[i] == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last element heap[index] = heap[heap.length - 1]; // Remove the last element heap.pop(); // Heapify the tree starting from the element at the deleted index while (true) { let left_child = 2 * index + 1; let right_child = 2 * index + 2; let smallest = index; if (left_child < heap.length && heap[left_child] < heap[smallest]) { smallest = left_child; } if (right_child < heap.length && heap[right_child] < heap[smallest]) { smallest = right_child; } if (smallest != index) { [heap[index], heap[smallest]] = [heap[smallest], heap[index]]; index = smallest; } else { break; } } } // Main function to test the insertMinHeap and deleteMinHeap functions let heap = []; let values = [13, 16, 31, 41, 51, 100]; for (let i = 0; i < values.length; i++) { insertMinHeap(heap, values[i]); } console.log('Initial heap: ' + heap.join(' ')); deleteMinHeap(heap, 13); console.log('Heap after deleting 13: ' + heap.join(' '));> Ieșire
Spațiu auxiliar: Pe)
3. Operațiune de vizualizare pe Structura de date Min-Heap:
Pentru a accesa elementul minim (adică rădăcina heap-ului), este returnată valoarea nodului rădăcină. Complexitatea timpului de peek într-un min-heap este O(1).
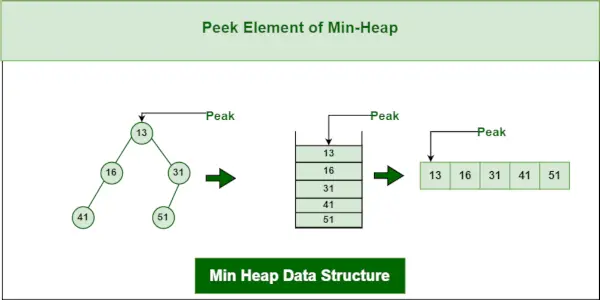
Structura de date Min Heap
Implementarea operațiunii Peek în Min-Heap:
C++ #include #include #include using namespace std; int main() { // Create a max heap with some elements using a // priority_queue priority_queue , mai mare > minHeap; minHeap.push(9); minHeap.push(8); minHeap.push(7); minHeap.push(6); minHeap.push(5); minHeap.push(4); minHeap.push(3); minHeap.push(2); minHeap.push(1); // Obține elementul de vârf (adică, cel mai mare element) int peakElement = minHeap.top(); // Imprimă valoarea maximă a elementului<< 'Peak element: ' << peakElement << std::endl; return 0; }> Java import java.util.PriorityQueue; public class GFG { public static void main(String[] args) { // Create a max heap with some elements using a // PriorityQueue PriorityQueue minHeap = new PriorityQueue(); minHeap.add(9); minHeap.add(8); minHeap.add(7); minHeap.add(6); minHeap.add(5); minHeap.add(4); minHeap.add(3); minHeap.add(2); minHeap.add(1); // Obține elementul de vârf (adică, cel mai mare element) int peakElement = minHeap.peek(); // Imprimă elementul de vârf System.out.println('Element de vârf: ' + peakElement); } }>>> using System; using System.Collections.Generic; public class GFG { public static void Main() { // Create a min heap with some elements using a // PriorityQueue var minHeap = new PriorityQueue (); minHeap.Enqueue(9); minHeap.Enqueue(8); minHeap.Enqueue(7); minHeap.Enqueue(6); minHeap.Enqueue(5); minHeap.Enqueue(4); minHeap.Enqueue(3); minHeap.Enqueue(2); minHeap.Enqueue(1); // Obține elementul de vârf (adică cel mai mic element) int peakElement = minHeap.Peek(); // Imprimă elementul de vârf Console.WriteLine('Element de vârf: ' + peakElement); } }>>> Ieșire
Într-un heap min implementat folosind un arbore binar, elementul de vârf poate fi accesat și în timp O(1), deoarece este întotdeauna situat la rădăcina arborelui.
Spațiu auxiliar: Pe)
4. Operațiune Heapify pe Min-Heap Data Structure:
O operație de heapify poate fi folosită pentru a crea un min heap dintr-o matrice nesortată. Acest lucru se realizează pornind de la ultimul nod care nu este frunză și efectuând în mod repetat operația de bule până când toate nodurile satisfac proprietatea heap.
Operațiune Heapify în Min Heap
Implementarea operațiunii Heapify în Min-Heap:
C++ #include #include using namespace std; void minHeapify(vector &arr, int i, int n) { int mai mic = i; int l = 2*i + 1; int r = 2*i + 2; dacă (l< n && arr[l] < arr[smallest]) smallest = l; if (r < n && arr[r] < arr[smallest]) smallest = r; if (smallest != i) { swap(arr[i], arr[smallest]); minHeapify(arr, smallest, n); } } int main() { vector arr = {10, 5, 15, 2, 20, 30}; cout<< 'Original array: '; for (int i = 0; i < arr.size(); i++) cout << arr[i] << ' '; // Perform heapify operation on min-heap for (int i = arr.size()/2 - 1; i>= 0; i--) minHeapify(arr, i, arr.size()); cout<< '
Min-Heap after heapify operation: '; for (int i = 0; i < arr.size(); i++) cout << arr[i] << ' '; return 0; }>
Java // Java code of Heapify operation in Min-Heap import java.util.Arrays; import java.util.List; public class Main { // Function to maintain the min-heap property of the heap rooted at index 'i' public static void minHeapify(List arr, int i, int n) { // Presupunem că rădăcina este cel mai mic element inițial int mai mic = i; // Calculați indicii fiului stâng și drept al nodului curent int l = 2 * i + 1; int r = 2 * i + 2; // Compară copilul din stânga cu cel mai mic actual dacă (l< n && arr.get(l) < arr.get(smallest)) smallest = l; // Compare the right child with the current smallest if (r < n && arr.get(r) < arr.get(smallest)) smallest = r; // If the current node is not the smallest, swap it with the smallest child if (smallest != i) { int temp = arr.get(i); arr.set(i, arr.get(smallest)); arr.set(smallest, temp); // Recursively heapify the subtree rooted at the smallest child minHeapify(arr, smallest, n); } } public static void main(String[] args) { // Create a list representing the array List arr = Arrays.asList(10, 5, 15, 2, 20, 30); System.out.print('Matrice originală: '); // Imprimă tabloul original pentru (int i = 0; i< arr.size(); i++) System.out.print(arr.get(i) + ' '); // Perform heapify operation on the min-heap // Start from the last non-leaf node and go up to the root of the tree for (int i = arr.size() / 2 - 1; i>= 0; i--) minHeapify(arr, i, arr.size()); System.out.print('
Min-Heap după operația de heapify: '); // Imprimă min-heap după operația de heapify pentru (int i = 0; i< arr.size(); i++) System.out.print(arr.get(i) + ' '); } }> Piton def minHeapify(arr, i, n): smallest = i left = 2 * i + 1 right = 2 * i + 2 if left < n and arr[left] < arr[smallest]: smallest = left if right < n and arr[right] < arr[smallest]: smallest = right if smallest != i: arr[i], arr[smallest] = arr[smallest], arr[i] minHeapify(arr, smallest, n) if __name__ == '__main__': arr = [10, 5, 15, 2, 20, 30] print('Original array:', arr) # Perform heapify operation on a min-heap for i in range(len(arr) // 2 - 1, -1, -1): minHeapify(arr, i, len(arr)) print('Min-Heap after heapify operation:', arr)> C# using System; using System.Collections.Generic; class GFG { // Function to perform the minHeapify operation on a min-heap. static void MinHeapify(List arr, int i, int n) { int mai mic = i; int stânga = 2 * i + 1; int dreapta = 2 * i + 2; // Compară copilul din stânga cu cel mai mic nod curent. dacă (stânga< n && arr[left] < arr[smallest]) smallest = left; // Compare the right child with the current smallest node. if (right < n && arr[right] < arr[smallest]) smallest = right; // If the current node is not the smallest // swap it with the smallest child. if (smallest != i) { int temp = arr[i]; arr[i] = arr[smallest]; arr[smallest] = temp; // Recursively call minHeapify on the affected subtree. MinHeapify(arr, smallest, n); } } static void Main(string[] args) { List arr = Listă nouă { 10, 5, 15, 2, 20, 30}; Console.Write('Matrice originală: '); foreach (int num in arr) Console.Write(num + ' '); // Efectuați operația heapify pe min-heap. pentru (int i = arr.Count / 2 - 1; i>= 0; i--) MinHeapify(arr, i, arr.Count); Console.Write('
Min-Heap după operația heapify: '); foreach (int num in arr) Console.Write(num + ' '); } }>>> Ieșire
5. Operațiune de căutare pe Structura de date Min-Heap:
Pentru a căuta un element în heap-ul min, se poate efectua o căutare liniară peste matricea care reprezintă heap-ul. Cu toate acestea, complexitatea în timp a unei căutări liniare este O(n), care nu este eficientă. Prin urmare, căutarea nu este o operațiune utilizată în mod obișnuit într-un heap min.
Iată un exemplu de cod care arată cum să căutați un element într-un heap min folosind std::find() :
C++ #include using namespace std; int main() { priority_queue , mai mare > min_heap; // exemplu heap maxim min_heap.push(10); min_heap.push(9); min_heap.push(8); min_heap.push(6); min_heap.push(4); int element = 6; // element pentru a căuta bool găsit = false; // Copiați heap-ul minim într-o coadă temporară și căutați // elementul std::priority_queue , mai mare > temp = min_heap; while (!temp.empty()) { if (temp.top() == element) { found = true; pauză; } temp.pop(); } if (găsit) { std::cout<< 'Element found in the min heap.' << std::endl; } else { std::cout << 'Element not found in the min heap.' << std::endl; } return 0; }> Java import java.util.PriorityQueue; public class GFG { public static void main(String[] args) { PriorityQueue min_heap = new PriorityQueue(); min_heap.add( 3); // inserați elemente în coada de prioritate min_heap.offer(1); min_heap.ofertă(4); min_heap.ofertă(1); min_heap.ofertă(6); int element = 6; // element de căutare boolean găsit = false; // Copiați heap-ul minim într-o coadă temporară și căutați // elementul PriorityQueue temp = new PriorityQueue(min_heap); while (!temp.isEmpty()) { if (temp.poll() == element) { found = true; pauză; } } if (găsit) { System.out.println( 'Element găsit în heap min.'); } else { System.out.println('Elementul nu a fost găsit în heap-ul min.'); } } }>>> using System; using System.Collections.Generic; public class GFG { public static void Main() { var minHeap = new PriorityQueue (); // exemplu min heap minHeap.Enqueue(4); minHeap.Enqueue(6); minHeap.Enqueue(8); minHeap.Enqueue(9); minHeap.Enqueue(10); int element = 6; // element pentru a căuta bool găsit = false; // Copiați heap-ul minim într-o coadă temporară și căutați // elementul var temp = new PriorityQueue (minHeap); while (temp.Count> 0) { if (temp.Peek() == element) { found = true; pauză; } temp.Dequeue(); } if (găsit) { Console.WriteLine( 'Element găsit în heap min.'); } else { Console.WriteLine('Elementul nu a fost găsit în heap-ul min.'); } } }>>> Ieșire
Operația de inserare are o complexitate de timp de O(log n) în cel mai rău caz, deoarece proprietatea heap trebuie menținută. Operația de căutare implică copierea cozii prioritare într-o coadă temporară și apoi traversarea cozii temporare, care necesită O(n log n) timp în cel mai rău caz, deoarece fiecare element trebuie copiat și scos din coadă, iar coada de prioritate trebuie reconstruită pentru fiecare operațiune.
The complexitatea spațiului al programului este Pe) deoarece stochează n elemente din coada de prioritate și creează o coadă temporară cu n elemente.
Aplicații ale structurii de date Min-Heap:
- Sortare heap: Heap min este folosit ca o componentă cheie în algoritmul de sortare heap, care este un algoritm de sortare eficient cu o complexitate de timp de O(nlogn).
- Coada prioritară: O coadă de prioritate poate fi implementată folosind o structură de date min heap în care elementul cu valoarea minimă este întotdeauna la rădăcină.
- Algoritmul lui Dijkstra: În algoritmul lui Dijkstra, o grămadă min este utilizată pentru a stoca vârfurile graficului cu distanța minimă de la vârful de pornire. Vârful cu distanța minimă este întotdeauna la rădăcina grămezii.
- Codare Huffman: În codarea Huffman, un heap min este folosit pentru a implementa o coadă de prioritate pentru a construi un cod de prefix optim pentru un anumit set de caractere.
- Îmbinați K tablouri sortate: Având în vedere K matrice sortate, le putem îmbina într-o singură matrice sortată eficient folosind o structură de date min heap.
Avantajele structurii de date min-heap:
- Inserare și ștergere eficientă : Min heap permite inserarea și ștergerea rapidă a elementelor cu o complexitate de timp de O(log n), unde n este numărul de elemente din heap.
- Preluare eficientă a elementului minim: Elementul minim dintr-un heap min este întotdeauna la rădăcina heap-ului, care poate fi recuperat în timp O(1).
- Spațiu eficient: Min heap este o structură de date compactă care poate fi implementată folosind o matrice sau un arbore binar, ceea ce o face eficientă în spațiu.
- Triere: Heap min poate fi folosit pentru a implementa un algoritm de sortare eficient, cum ar fi sortarea heap cu o complexitate de timp de O(n log n).
- Coada prioritară: Min heap poate fi folosit pentru a implementa o coadă de prioritate, unde elementul cu prioritatea minimă poate fi recuperat eficient în timp O(1).
- Versatilitate: Min heap are mai multe aplicații în informatică, inclusiv algoritmi grafici, compresie de date și sisteme de baze de date.
În general, min heap este o structură de date utilă și versatilă, care oferă operațiuni eficiente, eficiență în spațiu și are mai multe aplicații în informatică.