Lumea algoritmică este frumoasă, cu strategii și instrumente multiple dezvoltate non-stop pentru a răspunde nevoii de calcul de înaltă performanță. De fapt, atunci când algoritmii sunt inspirați de legile naturale, se observă rezultate interesante. Algoritmii evolutivi aparțin unei astfel de clase de algoritmi. Acești algoritmi sunt proiectați astfel încât să imite anumite comportamente, precum și trăsături evolutive ale genomului uman. Mai mult, un astfel de design algoritmic nu este limitat doar la oameni, ci poate fi inspirat și de comportamentul natural al anumitor animale. Scopul de bază al fabricării unor astfel de metodologii este de a oferi soluții realiste, relevante și totuși cu costuri reduse la problemele care sunt până acum de nerezolvat prin mijloace convenționale.
Diferite tehnici de optimizare au evoluat astfel pe baza unor astfel de algoritmi evolutivi și, prin urmare, au deschis domeniul metaeuristicii. Metaeuristică a fost derivat din două cuvinte grecești, și anume, Meta sens un nivel mai sus și heuriskein sens a găsi . Algoritmi precum Optimizarea roiului de particule (PSO) și Optimizarea coloniilor de furnici (ACO) sunt exemple de inteligență și metaeuristică a roiului. Scopul inteligenței roi este de a proiecta sisteme inteligente multi-agenți, inspirându-se din comportamentul colectiv al insectelor sociale, cum ar fi furnicile, termitele, albinele, viespile și alte societăți animale, cum ar fi stolurile de păsări sau școlile de pești.
Fundal:
Tehnica de optimizare a coloniilor de furnici este pur inspirată din căutând hrană comportamentul coloniilor de furnici, introdus pentru prima dată de Marco Dorigo în anii 1990. Furnicile sunt insecte eusociale care preferă supraviețuirea și întreținerea comunității decât ca specii individuale. Ei comunică între ei folosind sunet, atingere și feromoni. Feromonii sunt compuși chimici organici secretați de furnici care declanșează un răspuns social la membrii aceleiași specii. Acestea sunt substanțe chimice capabile să acționeze ca hormoni în afara corpului individului secretor, pentru a influența comportamentul indivizilor primitori. Deoarece majoritatea furnicilor trăiesc pe pământ, ele folosesc suprafața solului pentru a lăsa urme de feromoni care pot fi urmate (mirosate) de alte furnici.
Furnicile trăiesc în cuiburi comunitare, iar principiul de bază al ACO este de a observa mișcarea furnicilor din cuiburile lor pentru a căuta hrană pe cel mai scurt drum posibil. Inițial, furnicile încep să se miște aleatoriu în căutarea hranei în jurul cuiburilor lor. Această căutare randomizată deschide mai multe rute de la cuib la sursa de hrană. Acum, pe baza calității și cantității hranei, furnicile transportă o parte din hrană înapoi cu concentrația necesară de feromoni pe calea de întoarcere. În funcție de aceste încercări cu feromoni, probabilitatea de selectare a unei anumite căi de către următoarele furnici ar fi un factor de ghidare pentru sursa de hrană. Evident, această probabilitate se bazează pe concentrația, precum și pe rata de evaporare a feromonului. De asemenea, se poate observa că, deoarece rata de evaporare a feromonului este, de asemenea, un factor decisiv, lungimea fiecărei căi poate fi ușor de luat în considerare.
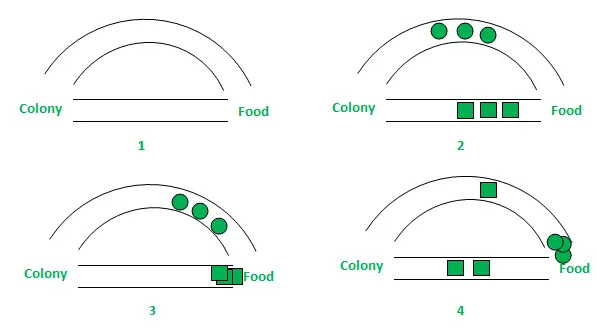
În figura de mai sus, pentru simplitate, au fost luate în considerare doar două căi posibile între sursa de hrană și cuibul de furnici. Etapele pot fi analizate astfel:
- Etapa 1: Toate furnicile sunt în cuibul lor. Nu există conținut de feromoni în mediu. (Pentru proiectarea algoritmică, cantitatea de feromoni reziduali poate fi luată în considerare fără a interfera cu probabilitatea) Etapa 2: Furnicile își încep căutarea cu o probabilitate egală (0,5 fiecare) de-a lungul fiecărei căi. În mod clar, calea curbă este mai lungă și, prin urmare, timpul necesar furnicilor pentru a ajunge la sursa de hrană este mai mare decât cealaltă. Etapa 3: Furnicile prin calea mai scurtă ajung mai devreme la sursa de hrană. Acum, evident că se confruntă cu o dilemă de selecție similară, dar de data aceasta din cauza traseului feromonilor de-a lungul drumului mai scurt deja disponibil, probabilitatea de selecție este mai mare. Etapa 4: Mai multe furnici se întorc pe calea mai scurtă și, ulterior, crește și concentrațiile de feromoni. Mai mult, din cauza evaporării, concentrația de feromoni pe calea mai lungă se reduce, scăzând probabilitatea de selecție a acestei căi în etapele ulterioare. Prin urmare, întreaga colonie folosește treptat calea mai scurtă cu probabilități mai mari. Deci, optimizarea căii este atinsă.
Design algoritmic:
Referitor la comportamentul de mai sus al furnicilor, acum poate fi dezvoltat un design algoritmic. Pentru simplitate, au fost luate în considerare o singură sursă de hrană și o singură colonie de furnici cu doar două căi de traversare posibilă. Întregul scenariu poate fi realizat prin grafice ponderate în care colonia de furnici și sursa de hrană acționează ca vârfuri (sau noduri); căile servesc drept margini, iar valorile feromonilor sunt greutățile asociate marginilor.
Fie graficul G = (V, E) unde V, E sunt muchiile și vârfurile graficului. Vârfurile conform considerației noastre sunt ÎNs (Sursa vârf – colonie de furnici) și ÎNd (Vertex de destinație – Sursă de hrană), Cele două margini sunt ȘI1 și ȘI2 cu lungimi L1 și L2 atribuite fiecăruia. Acum, se poate presupune că valorile feromonilor asociate (indicative pentru puterea lor). R1 și R2 pentru vârfurile E1și E2respectiv. Astfel, pentru fiecare furnică, probabilitatea de pornire a selecției căii (între E1și E2) poate fi exprimat astfel:
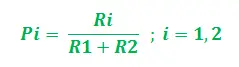
Evident, dacă R1>R2, probabilitatea de a alege E1este mai mare și invers. Acum, în timp ce te întorci pe această cale cea mai scurtă, spune Ei, valoarea feromonului este actualizată pentru calea corespunzătoare. Actualizarea se face pe baza lungimii căilor, precum și a ratei de evaporare a feromonului. Deci, actualizarea poate fi realizată în etape, după cum urmează:
- În funcție de lungimea căii -
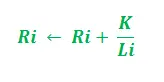
În actualizarea de mai sus, i = 1, 2 și „K” servesc ca parametru al modelului. Mai mult, actualizarea depinde de lungimea căii. Mai scurtă calea, cu atât feromonii adăugati sunt mai mari. În conformitate cu viteza de evaporare a feromonului -
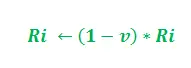
Parametrul „v” aparține intervalului (0, 1] care reglează evaporarea feromonilor. În plus, i = 1, 2.
La fiecare iterație, toate furnicile sunt plasate la vârful sursă Vs(colonie de furnici). Ulterior, furnicile se mută din Vsla Vd(sursă de hrană) urmând pasul 1. În continuare, toate furnicile își desfășoară călătoria de întoarcere și își consolidează calea aleasă pe baza pasului 2.
Pseudo cod:
Procedure AntColonyOptimization: Initialize necessary parameters and pheromone trials; while not termination do : Generate ant population; Calculate fitness values associated with each ant; Find best solution through selection methods; Update pheromone trial; end while end procedure>
Actualizarea feromonilor și calculele de fitness din pseudocodul de mai sus pot fi găsite prin implementările în pas menționate mai sus.
Astfel, a fost stabilită introducerea tehnicii de optimizare ACO. Aplicarea ACO poate fi extinsă la diverse probleme precum celebrele TSP (Problema vânzătorului călător) .
Referinte:
https://www.ics.uci.edu/~welling/teaching/271fall09/antcolonyopt.pdf
