Incentrul unui triunghi este punctul de intersecție al tuturor celor trei bisectoare ale unui triunghi. Incentrul este un punct important într-un triunghi în care liniile care taie unghiurile în jumătate se unesc. Acest punct este, de asemenea, centrul unui cerc numit Incircle care se potrivește perfect în interiorul triunghiului și atinge toate cele trei laturi la fel. Acest articol acoperă diferite concepte ale incentrului triunghiului, cum ar fi motivul pentru care acest punct este important, cum să-l găsiți folosind o busolă sau numere și proprietățile incentrului cercului.

Cuprins

• Ce este incentrul unui triunghi?
• Proprietățile unui incentrul unui triunghi
• Formula incentrului unui triunghi
• Cum să găsiți incentrul unui triunghi
• Centroid, circumcentru, incentru, ortocentru

Ce este incentrul unui triunghi?

Incentrul unui triunghi, după cum sugerează și numele, este punctul central al triunghiului. Acest punct pe care îl numim incentru se formează la joncțiunea în care se întâlnesc toate liniile care bisectează unghiurile interioare. Distanța punctului de toate cele trei laturi ale triunghiului este aceeași. Cercul triunghiului se potrivește și unui cerc perfect în interiorul triunghiului și acest cerc se numește cercul triunghiului.

Definiția incentrului

Incentrul unui triunghi este punctul din interiorul triunghiului în care se unesc toate cele trei linii care îi taie unghiurile interioare în jumătate. Acest punct este la aceeași distanță de cele trei laturi ale triunghiului, făcându-l ca mijlocul triunghiului. Este, de asemenea, centrul celui mai mare cerc care se poate încadra perfect în triunghi, pe care îl numim cerc. Pentru a simboliza incentrul, folosim de obicei litera I,

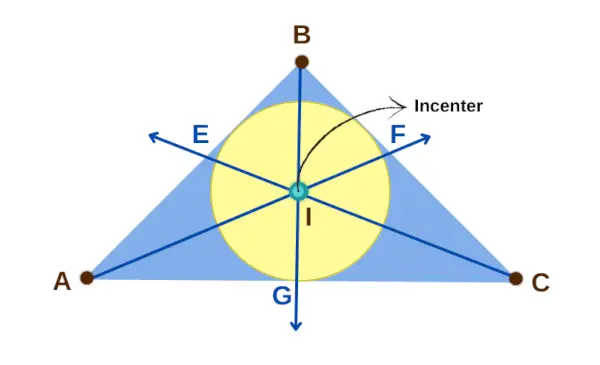
Incentrul unui triunghi

Proprietățile unui incentrul unui triunghi

Câteva proprietăți importante ale incentrului triunghiului sunt prezentate mai jos:

Proprietatea 1: Dacă eu este incentrul unui triunghi ABC, atunci trei perechi de segmente de dreaptă au lungime egală: AE și AG, CG și CF și BF și BE. Aceasta înseamnă că AE = AG, CG = CF și BF = BE.

sortare matrice java

Proprietatea 2: Incentrul eu are și o relație specială cu unghiurile triunghiului. Face ca unghiurile ∠BAI și ∠CAI să fie egale, ∠BCI și ∠ACI să fie egale și ∠ABI și ∠CBI să fie egale. Aceasta urmează teorema bisectoarei unghiului.

Proprietatea 3: Incentrul eu este centrul unui cerc care atinge toate cele trei laturi ale triunghiului și distanța de la eu la laturile triunghiului (EI, FI, GI) sunt toate la fel. Aceste distanțe sunt numite inradii sau raza cercului.

Proprietatea 4: Puteți calcula aria triunghiului folosind semiperimetrul (s) și inradiusul (r). Formula este A = sr, unde A este aria, s este semiperimetrul (s = (a + b + c)/2, unde a, b și c sunt lungimile laturilor triunghiului), iar r este inradius.

Proprietatea 5: Incentrul unui triunghi rămâne întotdeauna în interiorul triunghiului. Spre deosebire de ortocentrul, care poate fi în afara triunghiului în unele cazuri, incentrul este întotdeauna conținut în limitele triunghiului.

Formula incentrului unui triunghi

Formula pentru a găsi incentrul formulei cu 3 coordonate (x₁, și₁), (X₂, și₂), și (x₃, și₃) este:

{(topor ₁ + bx ₂ + cx ₃ )/(a + b + c), (este ₁ + de către ₂ + c ₃ )/(a + b + c)}

În termeni simpli, pentru a obține incentrul, trebuie să:

• Înmulțiți coordonata x a punctului A cu lungimea laturii a, coordonata x a punctului B cu lungimea laturii b și coordonata x a punctului C cu lungimea laturii c. Apoi, adăugați-le împreună.
• Împărțiți rezultatul la suma lungimilor laturilor a, b și c.
• Repetați același proces pentru coordonatele y, dar folosind lungimile laterale a, b și c.

Formula unghiului incentrului unui triunghi

Formula pentru a afla incentrul unui unghi al unui triunghi este următoarea:

Fie că Într-un triunghi D, F și G sunt punctele în care bisectoarele unghiurilor unghiurilor A, B și, respectiv, C, se întâlnesc cu laturile BC, AC și AB.

Unghiul ∠AIB (unde I este incentrul triunghiului) poate fi calculat folosind formula:

∠AIB = 180° – (jumătate din suma unghiurilor A și B)

SAU

∠AIB = 180° – (∠A + ∠B)/2

Cum să găsiți incentrul unui triunghi

Există două metode pentru a găsi incentrul unui triunghi. În construcție, localizăm incentrul desenând bisectoarele triunghiului. În geometria coordonatelor, folosim o formulă pentru a determina incentrul.

Folosind geometria coordonatelor : Găsiți incentrul triunghiului cu coordonatele date ca: A(2, 2), B(6, 2) și C(4, 5)

Conform informatiilor date

• (X₁, și₁) = (2, 2)
• (X₂, și₂) = (6, 2)
• (X₃, și₃) = (4, 5)

Știm că incentrul unui triunghi este:

I(x, y) = {(topor ₁ + bx ₂ + cx ₃ )/(a + b + c), (este ₁ + de către ₂ + c ₃ )/(a + b + c)}

Pentru latura a: Distanța dintre punctele B și C = √((6 – 4)²+ (2 – 5)²) = √8

Pentru latura b: Distanța dintre punctele A și C = √((2 – 4)²+ (2 – 5)²) = √13

Pentru latura c: Distanța dintre punctele A și B = √((6 – 2)²+ (2 – 2)²) = 4

Punând valorile lui a, b, c în formula incentrului, obținem:

I(x, y) = {(8×2 + 13×5 + 4×4)/(8 + 13 +4), (8×2 + 13×2 + 4×5)/(8 + 13 +4) )}

⇒ I(x, y) = (16 + 78 + 16)/(25), (16 + 26 + 20)/(25)

⇒ I(x, y) = (110/25, 62/25) = (22/5,62/25)

∴ Incentrul triunghiului ABC cu coordonatele este (22/5,62/25)

Cum se construiește incentrul unui triunghi?

Pentru a construi incentrul unui triunghi va fi nevoie să folosiți o busolă. Folosind o busolă, urmați pașii de mai jos:

Pasul 1: Puneți un capăt al busolei pe un vârf al triunghiului și celălalt capăt atinge o parte.

Pasul 2: Folosește busola pentru a desena două arce pe două laturi ale triunghiului.

Pasul 3: Cu aceeași distanță pe busolă, faceți două arce în interiorul triunghiului. Aceste arcuri ar trebui să se încrucișeze de unde ating părțile laterale.

Pasul 4: Desenați o linie de la vârful triunghiului până la locul în care cele două arce interioare se intersectează.

Pasul 5: Repetați aceiași pași de la celălalt vârf al triunghiului.

Pasul 6: Acolo unde cele două linii se întâlnesc sau se intersectează este incentrul triunghiului.

Incentrul triunghiului dreptunghic

Incentrul dacă a Triunghi dreptunghic este punctul în care se întâlnesc toate bisectoarele unui triunghi dreptunghic. Dacă laturile unui triunghi dreptunghic măsoară a, b și c, atunci raza cercului „r” este dată ca r = (ab)/(a + b + c). Incentrul triunghiului dreptunghic este ilustrat mai jos:

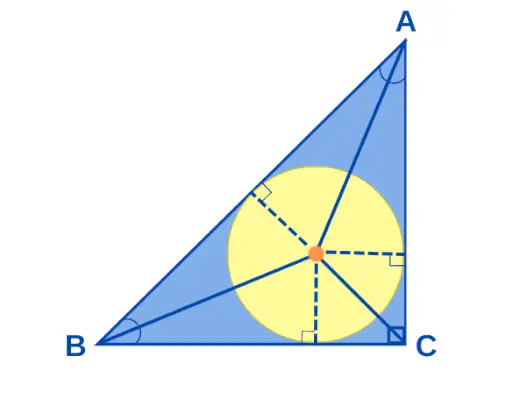
Incentrul unui triunghi dreptunghic

Centroid, circumcentru, incentru, ortocentru

Centroid, Circumcenter, Incenter și Orthocenter sunt cele patru puncte importante legate de un traingle. O comparație între Centroid, Circumcenter, Incenter și Orthocenter este tabelată mai jos:

De asemenea, verifica

• Aria triunghiului
• Perimetrul triunghiului
• Proprietatea Sumei unghiurilor a unui triunghi

Exemple de incentrul unui triunghi

Exemplul 1: Calculați incentrul triunghiului ABC. AB= 8cm, BC= 15 cm, CA= 17 cm.

Soluţie:

Folosind formula incentrului triunghiului = (aA + bB + cC)/(a + b + c)

Unde,

• a = 8
• b = 15
• c = 17

Și unghiurile sunt,

• A = 30°
• B = 60°
• C = 90°

Punând aceste valori în formula pentru a obține,

⇒ {(8)(30) + (15)(60) + (17)(90)}/{8 + 15 + 17}

⇒ (240 + 900 + 1530)/40

⇒ 2670/40

⇒ 66,75

Exemplul 2: Jane a calculat aria unui câmp triunghiular ca fiind de 120 de metri pătrați. Perimetrul terenului este de 36 de metri. Dacă un cerc este desenat în interiorul triunghiului astfel încât să atingă fiecare parte a triunghiului, ajută-l pe Jane să calculeze raza triunghiului.

Soluţie:

Conform informațiilor furnizate,

Aria triunghiului = 120 de metri pătrați

Perimetrul triunghiului = 36 metri

Știm, aria unui triunghi = r × s

s = semiperimetru

s = p/2 = 36/2 = 18

A = r × s

r = A/s

r = 120/18

r = 6,67 metri

Practicați probleme pe incentrul unui triunghi

Problema 1: dat triunghiul PQR cu vârfurile P(1, 2), Q(4, 6) și R(7, 2), găsiți coordonatele incentrului.

Problema 2: Construiți un triunghi ABC cu ∠A = 45°, ∠B = 60° și ∠C = 75°. Utilizați metoda de construcție pentru a găsi incentrul.

Problema 3: În triunghiul LMN, dacă ∠L = 75°, ∠M = 60° și ∠N = 45°, găsiți coordonatele incentrului.

Problema 4: Construiți un triunghi XYZ cu ∠X = 80°, ∠Y = 50° și ∠Z = 50°. Utilizați metoda de construcție pentru a găsi incentrul.

Incentrul unui triunghi: Întrebări frecvente

Ce este incentrul unui triunghi?

Incentrul unui triunghi este punctul în care bisectoarele unghiurilor interioare se intersectează. Este echidistant de toate cele trei laturi ale triunghiului.

Care este semnificația incentrului într-un triunghi?

Incentrul este semnificativ deoarece este centrul cercului triunghiului, cel mai mare cerc care se potrivește în interiorul triunghiului. Are proprietatea de a fi echidistant din toate părțile.

bash dacă altceva

Incenterul poate fi în afara triunghiului?

Nu, incentrul este întotdeauna în interiorul triunghiului. Este punctul de concurență pentru bisectoarele unghiului și, prin definiție, trebuie să fie în limitele triunghiului.

Cum este construit Incenterul folosind o busolă și o muchie dreaptă?

Pentru a construi incentrul, folosiți o busolă pentru a desena bisectoare de la fiecare vârf spre partea opusă. Incentrul este punctul în care aceste bisectoare se intersectează.

Ce este Formula Incenter?

Formula pentru incentrul unui triunghi se poate scrie ca:

frac{(aA+bB+cC)}{a+b+c}

Care sunt proprietățile centrului unui triunghi?

Incentrul are câteva proprietăți cheie. Este echidistant de laturile triunghiului, ceea ce înseamnă că distanțele față de laturi sunt egale. De asemenea, este punctul de intersecție al bisectoarelor unghiurilor, împărțind unghiurile în două părți egale.

Cum este determinat incentrul?

Pentru a determina incentrul, trebuie să găsiți unde se intersectează bisectoarele unghiului. Acest lucru se poate face folosind formula incentrului sau prin desenarea bisectoarelor unghiului și găsirea punctului de intersecție al acestora.

Care este diferența dintre centru și circumcentru?

Principala diferență dintre incentru și circumcentru este focalizarea lor. Incentrul se ocupă de bisectoare unghiulare și este centrul cercului înscris, în timp ce circumcentrul se ocupă de bisectoare perpendiculare și este centrul cercului circumscris.

Este Incentru și Centroid la fel?

Nu, incentrul și centroidul sunt diferite. Incentrul este locul în care bisectoarele unghiului se întâlnesc, în timp ce centroidul este locul în care medianele se intersectează. Medianele conectează vârfurile la mijlocul părții opuse.

Centrul și Ortocentrul sunt la fel?

Nu, incentrul și ortocentrul nu sunt la fel. Incentrul este punctul în care unghiul se biectează, în timp ce ortocentrul implică altitudini – linii de la fiecare vârf perpendicular pe latura opusă. Sunt puncte diferite dintr-un triunghi.