logo

TechCodeview

Regresia procesului gaussian (GPR)

Problemele de regresie și clasificare probabilistică pot fi rezolvate folosind procesul Gaussian (GP), o tehnică de învățare supravegheată. Deoarece fiecare proces gaussian poate fi gândit ca o generalizare infinit-dimensională a multivariatelor distribuții gaussiene , termenul Gaussian apare în nume. Vom discuta despre procesele gaussiene pentru regresie în această postare, care este denumită și regresia procesului gaussian (GPR). Numeroase probleme din lumea reală din domeniile științei materialelor, chimiei, fizicii și biologiei au fost rezolvate cu ajutorul GPR.

Cuprins



Regresia procesului gaussian (GPR)

Regresia procesului gaussian (GPR) este o tehnică de regresie neparametrică puternică și flexibilă utilizată în învățare automată și statistici . Este deosebit de util atunci când se confruntă cu probleme care implică date continue, unde relația dintre variabilele de intrare și ieșire nu este cunoscută în mod explicit sau poate fi complexă. GPR este o abordare bayesiană care poate modela certitudinea în predicții, făcându-l un instrument valoros pentru diverse aplicații, inclusiv optimizare, prognoza serii de timp și multe altele. GPR se bazează pe conceptul unui proces Gaussian, care este o colecție de variabile aleatoare, dintre care orice număr finit are o distribuție Gaussiană comună. Un proces gaussian poate fi gândit ca o distribuție de funcții.

Concepte cheie ale regresiei proceselor gaussiene (GPR)

Procesul Gaussain

Un model probabilistic neparametric numit a Procesul Gaussian (GP) este utilizat în statistici și învățarea automată pentru regresie, clasificare și cuantificarea incertitudinii. Acesta descrie un grup de variabile aleatoare, fiecare dintre ele având o distribuție Gaussiană comună și poate avea un număr finit. GP-urile sunt o tehnică versatilă și eficientă pentru modelarea relațiilor complicate în date și producerea de prognoze cu incertitudinea asociată.

Caracteristicile proceselor gaussiene :



  • Natura neparametrică : Medicii de familie se pot adapta la complexitatea datelor deoarece nu se bazează pe un număr stabilit de parametri ai modelului
  • Predicții probabilistice : Predicțiile de la medicii de familie pot fi cuantificate deoarece oferă predicții ca distribuții de probabilitate.
  • Interpolare și netezire : GP-urile sunt utile pentru date zgomotoase sau eșantionate neregulat, deoarece sunt bune la netezirea datelor zgomotoase și la interpolarea între punctele de date.
  • Marginalizarea hiperparametrilor : Prin eliminarea cerinței de ajustare explicită a hiperparametrilor, aceștia marginalizează hiperparametrii, simplificând modelul.

Funcția medie

Valoarea prezisă a funcției care este modelată la fiecare punct de intrare este reprezentată de funcţie medie în procesele gaussiene (GP). Funcționează ca o prezumție fundamentală cu privire la structura de date subiacentă. Funcția medie este adesea setată la zero în mod implicit, nu neapărat și poate fi modificată în funcție de proprietățile datelor sau de expertiza domeniului. Prin influențarea tendinței centrale a previziunilor, îi ajută pe medicii generaliști să identifice modele sau tendințe în date. GP oferă predicții probabilistice care conțin incertitudine, precum și estimări punctuale prin includerea funcției medii

Funcția de covarianță (kernel).

The funcția de covarianță , denumită și funcție kernel, măsoară cât de similare sunt punctele de date de intrare între ele în procesele gaussiene (GP). Este esențială în caracterizarea comportamentului modelului GP, afectând selecția funcțiilor din distribuția anterioară. Funcția de covarianță măsoară asemănările pe perechi pentru a stabili corelația dintre valorile funcției. Medicii de familie se pot adapta la o gamă largă de modele de date, de la tendințe netede la structuri complexe, deoarece diferitele funcții ale nucleului captează diferite tipuri de corelații. Performanța modelului poate fi foarte afectată de selecția nucleului.

Distribuții anterioare

The distributie prealabila , în procesele gaussiene (GPs), este înțelegerea noastră a funcțiilor înainte de observarea oricăror date. De obicei, este descrisă printr-o funcție de covarianță (nucleu) și o funcție medie. În timp ce funcția de covarianță descrie asemănarea sau corelația dintre valorile funcției la diferite puncte de intrare, funcția medie codifică așteptările noastre anterioare. Acesta este folosit în prealabil de către medicii de familie pentru a crea o distribuție între funcții. În GP, ​​prioritățile pot fi selectate pentru a reprezenta incertitudinea datelor, pentru a integra cunoștințele de domeniu sau pentru a indica netezimea.



Distribuții posterioare

procese gaussiene” distribuție ulterioară arată ipotezele noastre revizuite despre funcții după observarea datelor. Reunește probabilitatea datelor date în funcție de funcție și distribuția anterioară. Posterior în regresia GP oferă o distribuție pe funcții care se potrivesc cel mai bine cu datele observate. Permițând predicții probabilistice și cuantificarea incertitudinii, distribuția posterioară reflectă compromisul dintre credințele anterioare stocate în distribuția anterioară și informațiile furnizate de date.

Conceptul matematic al regresiei proceselor gaussiene (GPR)

Pentru sarcinile de regresie, se folosește un model de învățare automată probabilistic, non-parametric, numit regresie Gaussian Process (GP). Atunci când modelați interacțiuni complexe și ambigue între variabilele de intrare și de ieșire, este un instrument puternic. Se presupune că o distribuție Gaussiană multivariată produce punctele de date în regresia GP, iar obiectivul este de a deduce această distribuție.

Modelul de regresie GP are următoarea expresie matematică. Să presupunem x1, X2,…..,Xnsunt punctele de date de intrare, unde x aparțin numerelor reale (-2,-1,0,1...), (xiepsilon R)

Să presupunem că y1, și2,……., șinsunt valorile de ieșire, unde yiaparține numărului real (yiepsilon R)

Modelul de regresie GP presupune că un proces gaussian cu o funcție medie (mu ) și funcția de covarianță (k) furnizează funcția f care conectează intrările la ieșiri.

Apoi, la un set de locații de testare x*, distribuția lui f este dată de:

f(x^*) ∼ N(mu(x^*), k(x^*, x^*))

În mod obișnuit, funcțiile nucleului sunt utilizate pentru a defini funcția medie și funcția de covarianță. Ca o ilustrare, nucleul exponențial pătrat care este folosit frecvent este descris ca:

tipuri de date sql

k(x_{i},x_{j}) = sigma^2 exp(-frac{||x_{i} – x_{j}||^2}{2l^2})

Unde,

  • k(x_{i}, x_{j}) = Funcția kernel este reprezentată prin aceasta și calculează corelația sau asemănarea dintre două puncte de date de intrare, xiși xj.
  • sigma^2 = Parametrul de varianță al nucleului este acesta. Stabilește scara sau răspândirea verticală a funcției kernel. Reglează cât de puternic sunt corelate punctele de date. Un mai înaltsigma^2 produce o funcție de nucleu cu varianță mai mare.
  • exp: Funcția exponențială este responsabilă pentru ridicarea e la puterea argumentului.
  • ||x_{i} – x_{j}||^2 : Diferența dintre punctele de date de intrare, xiși xj, este distanța euclidiană la pătrat. Se măsoară separația geometrică dintre punctele din spațiul caracteristic.
  • l2: Aceasta este o reprezentare a scalei de lungime a nucleului sau a lungimii caracteristice. Reglează rata cu care funcția nucleului se deteriorează pe măsură ce punctele de date sunt mai îndepărtate. Un l mai mic face ca nucleul să se degradeze mai repede.

Modelul de regresie GP aplică inferența bayesiană pentru a determina distribuția lui f care este cel mai probabil să fi produs datele având în vedere un set de date de antrenament (x, y). Pentru a face acest lucru, trebuie calculată distribuția posterioară a lui f date fiind datele, care este definită după cum urmează:

p(f|x,y) =frac x,f)p(f) x)

unde probabilitatea marginală a datelor este p(y|x), distribuția anterioară a lui f este p(f), iar probabilitatea datelor dată de funcția f este (y|x,f).

După ce învață distribuția posterioară a lui f, modelul calculează distribuția predictivă posterioară pentru a face predicții la punctele de testare suplimentare x*. Poate fi definit astfel:

p(f^*|x^*, y,x) = int p(f^*|x^*, f), p(f|y,x)df

Unde,

  • p(f^*|x*, y, x) = Aceasta arată, având în vedere datele de antrenament y și x, probabilitatea condiționată a valorilor funcției prezise f*la un nou punct de intrare x*Altfel spus, este distribuția probabilității pentru toate valorile potențiale ale funcției la noul site de intrare x*, condiționat de datele observate y și de locațiile lor de intrare potrivire x.
  • int p(f^*|x^*, f)p(f|y,x)df = O integrală este folosită în această secțiune a ecuației pentru a determina probabilitatea condiționată. Integrala cuprinde toate valorile potențiale ale funcției f.
  • p(f^*|x^*, f) = Aceasta este distribuția de probabilitate condiționată a valorilor așteptate ale funcției f*la x*, având în vedere valorile funcției f în unele locații intermediare.
  • p(f|y,x) = Având în vedere datele observate (y) și locațiile lor de intrare (x), aceasta este distribuția de probabilitate condiționată a valorilor funcției (f).

Pentru sarcini precum luarea deciziilor conștientă de incertitudine și învățarea activă, această distribuție oferă o măsură a incertitudinii predicției, care poate fi utilă.

Etape în regresia procesului gaussian

  • Colectare de date : Adunați perechile de date intrare-ieșire pentru problema dvs. de regresie.
  • Alegeți o funcție Kernel : Selectați o funcție de covarianță adecvată (nucleul) care se potrivește problemei dvs. Alegerea nucleului influențează forma funcțiilor pe care GPR le poate modela.
  • Optimizarea parametrilor : Estimați hiperparametrii funcției kernel prin maximizarea probabilității datelor. Acest lucru se poate face folosind tehnici de optimizare precum coborârea gradientului.
  • Predicție: Având o nouă intrare, utilizați modelul GPR antrenat pentru a face predicții. GPR furnizează atât media prezisă, cât și incertitudinea asociată (varianță).

Implementarea regresiei procesului gaussian (GPR)

Piton import numpy as np import matplotlib.pyplot as plt from sklearn.gaussian_process import GaussianProcessRegressor from sklearn.gaussian_process.kernels import RBF from sklearn.model_selection import train_test_split # Generate sample data np.random.seed(0) X = np.sort(5 * np.random.rand(80, 1), axis=0) y = np.sin(X).ravel() # Add noise to the data y += 0.1 * np.random.randn(80) # Define the kernel (RBF kernel) kernel = 1.0 * RBF(length_scale=1.0) # Create a Gaussian Process Regressor with the defined kernel gp = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=10) # Split the data into training and testing sets X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.5, random_state=0) # Fit the Gaussian Process model to the training data gp.fit(X_train, y_train) # Make predictions on the test data y_pred, sigma = gp.predict(X_test, return_std=True) # Visualize the results x = np.linspace(0, 5, 1000)[:, np.newaxis] y_mean, y_cov = gp.predict(x, return_cov=True) plt.figure(figsize=(10, 5)) plt.scatter(X_train, y_train, c='r', label='Training Data') plt.plot(x, y_mean, 'k', lw=2, zorder=9, label='Predicted Mean') plt.fill_between(x[:, 0], y_mean - 1.96 * np.sqrt(np.diag(y_cov)), y_mean + 1.96 * np.sqrt(np.diag(y_cov)), alpha=0.2, color='k', label='95% Confidence Interval') plt.xlabel('X') plt.ylabel('y') plt.legend() plt.show()>

Ieșire:

gpr-Geeksforgeeks

În acest cod, mai întâi generați câteva puncte de date eșantion cu zgomot adăugat, apoi definiți un nucleu RBF și creați un Regressor de proces gaussian Cu acesta. Modelul este antrenat pe datele de antrenament și utilizat pentru a face predicții asupra datelor de testare. În cele din urmă, rezultatele sunt vizualizate cu un grafic care arată datele de antrenament, media prezisă și intervalul de încredere de 95%.

Implementarea procesului Gaussian în Python

Scikit Learn

Piton import matplotlib.pyplot as plt import numpy as np from scipy import linalg from sklearn.gaussian_process import kernels,GaussianProcessRegressor ## check version import sys import sklearn print(sys.version) !python --version print("numpy:", np.__version__) print("sklearn:",sklearn.__version__)>

Bibliotecile necesare pentru regresia procesului gaussian (GPR) în Python sunt importate de acest cod; acestea sunt SciPy pentru funcții de algebră liniară, NumPy pentru operații numerice și Matplotlib pentru vizualizarea datelor. Pentru a se asigura că este compatibil cu pachetele necesare, verifică suplimentar versiunea Python și o tipărește, împreună cu versiunile NumPy și scikit-learn (sklearn).

Selectarea Kernelului

Piton np.random.seed(0) n=50 kernel_ =[kernels.RBF (), kernels.RationalQuadratic(), kernels.ExpSineSquared(periodicity=10.0), kernels.DotProduct(sigma_0=1.0)**2, kernels.Matern() ] print(kernel_, ' ')>

Ieșire:

[RBF(length_scale=1),
RationalQuadratic(alpha=1, length_scale=1),
ExpSineSquared(length_scale=1, periodicity=10),
DotProduct(sigma_0=1) ** 2,
Matern(length_scale=1, nu=1.5)]

Codul specifică numărul de locuri de testare (n) și inițializează a sămânță aleatorie . Pentru a afișa nucleele alese, generează o listă cu mai multe funcții ale nucleului și tipărește lista.

Compararea și vizualizarea kernelului

Piton for kernel in kernel_: # Gaussian process gp = GaussianProcessRegressor(kernel=kernel) # Prior x_test = np.linspace(-5, 5, n).reshape(-1, 1) mu_prior, sd_prior = gp.predict(x_test, return_std=True) samples_prior = gp.sample_y(x_test, 3) # plot plt.figure(figsize=(10, 3)) plt.subplot(1, 2, 1) plt.plot(x_test, mu_prior) plt.fill_between(x_test.ravel(), mu_prior - sd_prior, mu_prior + sd_prior, color='aliceblue') plt.plot(x_test, samples_prior, '--') plt.title('Prior') # Fit x_train = np.array([-4, -3, -2, -1, 1]).reshape(-1, 1) y_train = np.sin(x_train) gp.fit(x_train, y_train) # posterior mu_post, sd_post = gp.predict(x_test, return_std=True) mu_post = mu_post.reshape(-1) samples_post = np.squeeze(gp.sample_y(x_test, 3)) # plot plt.subplot(1, 2, 2) plt.plot(x_test, mu_post) plt.fill_between(x_test.ravel(), mu_post - sd_post, mu_post + sd_post, color='aliceblue') plt.plot(x_test, samples_post, '--') plt.scatter(x_train, y_train, c='blue', s=50) plt.title('Posterior') plt.show() print("gp.kernel_", gp.kernel_) print("gp.log_marginal_likelihood:", gp.log_marginal_likelihood(gp.kernel_.theta)) print('-'*50, ' ')>

Ieșire:

RBF

graficul-1-Geeksforgeeks

gp.kernel_ RBF(length_scale=1,93)
gp.log_marginal_probabilitate: -3.444937833462133
-------------------------------------------------- -

Quadratic rațional

graficul-2-Geeksforgeeks

gp.kernel_ RationalQuadratic(alpha=1e+05, length_scale=1,93)
gp.log_marginal_probabilitate: -3.4449718909150966
--------------------------------------------------

ExpSineSquared

graficul-3-Geeksforgeeks

gp.kernel_ ExpSineSquared(length_scale=0,000524, periodicity=2,31e+04)
gp.log_marginal_probabilitate: -3.4449381454930217
--------------------------------------------------

Produs punct

graficul-4-Geeksforgeeks

gp.kernel_ DotProduct(sigma_0=0,998) ** 2
gp.log_marginal_probabilitate: -150204291.56018084
--------------------------------------------------

Matern

graficul-5-Geeksforgeeks

gp.kernel_ Matern(length_scale=1,99, nu=1,5)
gp.log_marginal_probabilitate: -5.131637070524745
--------------------------------------------------

Codul începe prin bucla peste diferitele funcții kernel listate în lista kernel_. Un regresor de proces gaussian (gp) este realizat folosind nucleul special pentru fiecare nucleu. Pentru Procesul Gaussian, aceasta stabilește structura de covarianță. Pentru a evalua distribuția anterioară se stabilește un set de puncte de intrare de test numit x_test, cu valori cuprinse între -5 și 5. Acest set de puncte este transformat într-un vector coloană.

Folosind metoda gp.predict, media distribuției anterioare (mu_prior) și abaterea standard (sd_prior) sunt determinate la fiecare punct de testare. Valorile deviației standard sunt solicitate folosind opțiunea return_std=True. gp.sample_y (x_test, 3) este folosit pentru a obține trei eșantioane de funcție din distribuția anterioară.

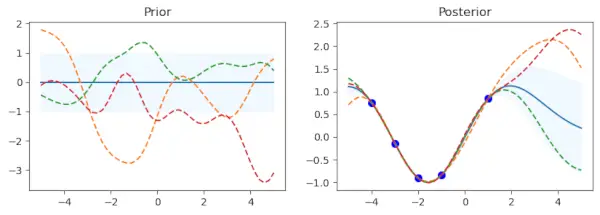
Primul subplot arată media distribuției anterioare, cu abaterea standard reprezentată de o zonă umbrită. Eșantioanele sunt suprapuse ca linii întrerupte, în timp ce media este afișată ca o linie continuă. Există un subplot numit Prior. Există un set definit de puncte de date de antrenament (x_train) și valori de obiectiv (y_train) care le însoțesc. Modelul Procesului Gaussian este ajustat folosind aceste puncte (gp.fit(x_train, y_train)). Cinci puncte de date cu valori sinusoidale corespunzătoare alcătuiesc datele de antrenament din acest cod.

După faza de adaptare a datelor de antrenament, procedura calculează media distribuției posterioare (mu_post) și abaterea standard (sd_post) pentru aceleași puncte de testare (x_test). gp.sample_y(x_test, 3) este, de asemenea, folosit pentru a produce mostre de funcții din distribuția posterioară. Al doilea subplot suprapune funcțiile eșantionate ca linii punctate și arată media distribuției posterioare, umbrită cu deviația standard. În albastru sunt reprezentate punctele de date de antrenament. Subplotul poartă numele Posterior.

Pentru a vedea diagramele anterioare și posterioare pentru nucleul curent și pentru a obține o înțelegere vizuală a comportamentului modelului, apelați funcția plt.show() a lui Matplotlib.

Codul arată detalii despre nucleul curent, cum ar fi gp.kernel_, care indică nucleul curent utilizat și gp.log_marginal_probabilitate (gp.kernel_.theta), care oferă probabilitatea log-marginală a modelului care utilizează nucleul curent, după fiecare set de diagrame anterioare și posterioare.

Avantajele regresiei procesului gaussian (GPR)

Regresia procesului gaussian (GPR) are o serie de beneficii într-o serie de aplicații:

  • GPR oferă un cadru probabilistic pentru regresie, ceea ce înseamnă că nu oferă doar estimări punctuale, ci oferă și estimări ale incertitudinii pentru predicții.
  • Este foarte flexibil și poate capta relații complexe în date.
  • GPR poate fi adaptat la diverse aplicații, inclusiv prognoza în serie de timp, optimizare și optimizare bayesiană.

Provocările regresiei procesului gaussian (GPR)

  • GPR poate fi costisitor din punct de vedere computațional atunci când se lucrează cu seturi de date mari, deoarece este necesară inversarea unei matrice de covarianță.
  • Alegerea funcției de nucleu și a hiperparametrilor săi pot avea un impact semnificativ asupra performanței modelului.

Exemple bune de aplicații GPR

  • Predicția prețului acțiunilor: GPR poate fi folosit pentru a modela și prezice prețurile acțiunilor, ținând cont de volatilitatea și incertitudinea de pe piețele financiare.
  • Experimente pe calculator: GPR este util în optimizarea simulărilor complexe prin modelarea relațiilor de intrare-ieșire și prin identificarea celor mai influenți parametri.
  • Detectarea anomaliilor: GPR poate fi aplicat la detectarea anomaliilor, unde identifică modele neobișnuite în datele din seria temporală prin captarea distribuțiilor normale de date.

Concluzie

În concluzie, regresia procesului gaussian este un instrument valoros pentru analiza și predicția datelor în situațiile în care înțelegerea incertitudinii în predicții este esențială. Prin valorificarea modelării probabilistice și a funcțiilor kernelului, GPR poate oferi rezultate precise și interpretabile. Cu toate acestea, este esențial să luați în considerare costul de calcul și nevoia de intervenție a experților atunci când implementați GPR în practică.