Exemplul 1:
Proiectați un NFA pentru tabelul de tranziție, după cum este prezentat mai jos:
| Starea actuală | 0 | 1 |
|---|---|---|
| →q0 | q0, q1 | q0, q2 |
| q1 | q3 | e |
| q2 | q2, q3 | q3 |
| →q3 | q3 | q3 |
Soluţie:
lista comparabila
Diagrama de tranziție poate fi desenată utilizând funcția de mapare, așa cum este prezentată în tabel.
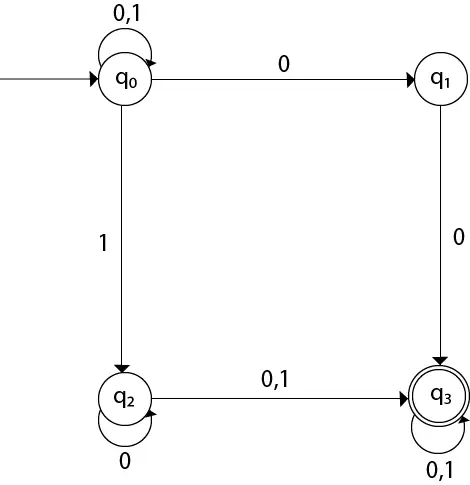
Aici,
δ(q0, 0) = {q0, q1} δ(q0, 1) = {q0, q2} Then, δ(q1, 0) = {q3} Then, δ(q2, 0) = {q2, q3} δ(q2, 1) = {q3} Then, δ(q3, 0) = {q3} δ(q3, 1) = {q3} Exemplul 2:
Proiectați un NFA cu ∑ = {0, 1} acceptă toate șirurile care se termină cu 01.
Soluţie:

Prin urmare, NFA ar fi:

Exemplul 3:
Proiectați un NFA cu ∑ = {0, 1} în care „1” dublu este urmat de „0” dublu.
Soluţie:
FA cu dublu 1 este după cum urmează:

Ar trebui să fie urmată imediat de 0 dublu.
Apoi,

Acum, înainte de dublu 1, poate exista orice șir de 0 și 1. În mod similar, după dublu 0, poate exista orice șir de 0 și 1.
Prin urmare, NFA devine:

Acum luând în considerare șirul 01100011
q0 → q1 → q2 → q3 → q4 → q4 → q4 → q4
Exemplul 4:
Proiectați un NFA în care toate șirurile să conțină un subșir 1110.
Soluţie:
Limbajul este format din tot șirul care conține subșirul 1010. Diagrama de tranziție parțială poate fi:

Acum, ca 1010 ar putea fi subșirul. Prin urmare, vom adăuga intrările 0 și 1, astfel încât subșirul 1010 al limbajului să poată fi menținut. Prin urmare, NFA devine:

Tabelul de tranziție pentru diagrama de tranziție de mai sus poate fi prezentat mai jos:
| Starea actuală | 0 | 1 |
|---|---|---|
| →q1 | q1 | q1, q2 |
| q2 | q3 | |
| q3 | q4 | |
| q4 | q5 | *q5 | q5 | q5 |
Luați în considerare un șir 111010,
δ(q1, 111010) = δ(q1, 1100) = δ(q1, 100) = δ(q2, 00)
M-am blocat! Deoarece nu există o cale de la q2 pentru simbolul de intrare 0. Putem procesa șirul 111010 într-un alt mod.
δ(q1, 111010) = δ(q2, 1100) = δ(q3, 100) = δ(q4, 00) = δ(q5, 0) = δ(q5, ε)
Deoarece starea q5 este starea de acceptare. Am scanat complet și am ajuns la starea finală.
Exemplul 5:
Proiectați un NFA cu ∑ = {0, 1} acceptă toate șirurile în care al treilea simbol de la capătul din dreapta este întotdeauna 0.
Soluţie:

Astfel, obținem cel de-al treilea simbol de la capătul drept ca „0” întotdeauna. NFA poate fi:

Imaginea de mai sus este un NFA deoarece în starea q0 cu intrarea 0, putem merge fie la starea q0, fie la q1.
