Divide and Conquer este un model algoritmic. În metodele algoritmice, proiectarea constă în a lua o dispută asupra unei intrări uriașe, a diviza intrarea în bucăți minore, a decide problema pentru fiecare dintre bucățile mici și apoi a îmbina soluțiile pe bucăți într-o soluție globală. Acest mecanism de rezolvare a problemei se numește Strategia Divide & Conquer.

Algoritmul Divide and Conquer constă într-o dispută folosind următorii trei pași.

Divideproblema inițială într-un set de subprobleme.A cuceri:Rezolvați fiecare subproblemă individual, recursiv.Combina:Adunați soluțiile subproblemelor pentru a obține soluția întregii probleme.

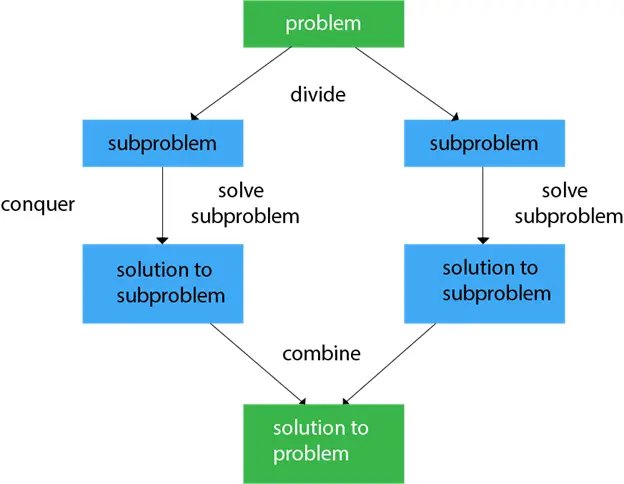
În general, putem urmări diviza și cuceri abordare într-un proces în trei etape.

Exemple: Algoritmii specifici de computer se bazează pe abordarea Divide & Conquer:

1. Problemă maximă și minimă
2. Căutare binară
3. Sortare (sortare îmbinare, sortare rapidă)
4. Turnul din Hanoi.

Elementele fundamentale ale strategiei Divide & Conquer:

Există două elemente fundamentale ale strategiei Divide & Conquer:

1. Formula relațională
2. Condiție de oprire

1. Formula relațională: Este formula pe care o generăm din tehnica dată. După generarea formulei, aplicăm strategia D&C, adică eliminăm problema recursiv și rezolvăm subproblemele rupte.

2. Condiție de oprire: Când rezolvăm problema utilizând strategia Divide & Conquer, atunci trebuie să știm că pentru cât timp, trebuie să aplicăm divide & Conquer. Deci condiția în care necesitatea de a opri pașii noștri recursivi ai D&C este numită Condiție de oprire.

Aplicații ale abordării Divide and Conquer:

Următorii algoritmi se bazează pe conceptul tehnicii Divide and Conquer:

Căutare binară:Algoritmul de căutare binar este un algoritm de căutare, care se mai numește și căutare pe jumătate de interval sau căutare logaritmică. Funcționează prin compararea valorii țintă cu elementul din mijloc existent într-o matrice sortată. După efectuarea comparației, dacă valoarea diferă, atunci jumătatea care nu poate conține ținta va fi eliminată în cele din urmă, urmată de continuarea căutării pe cealaltă jumătate. Vom lua în considerare din nou elementul de mijloc și îl vom compara cu valoarea țintă. Procesul continuă să se repete până la atingerea valorii țintă. Dacă am constatat că cealaltă jumătate este goală după încheierea căutării, atunci se poate concluziona că ținta nu este prezentă în matrice.Sortare rapida:Este cel mai eficient algoritm de sortare, cunoscut și sub numele de sortare cu schimb de partiții. Începe prin selectarea unei valori pivot dintr-o matrice, urmată de împărțirea restului elementelor matricei în două sub-matrice. Partiția se realizează comparând fiecare dintre elemente cu valoarea pivotului. Compară dacă elementul deține o valoare mai mare sau mai mică decât pivotul și apoi sortează tablourile recursiv.Sortare îmbinare:Este un algoritm de sortare care sortează o matrice făcând comparații. Începe prin împărțirea unei matrice în sub-matrice și apoi sortează recursiv fiecare dintre ele. După ce sortarea este finalizată, le îmbină înapoi.Cea mai apropiată pereche de puncte:Este o problemă de geometrie computațională. Acest algoritm pune accentul pe aflarea celei mai apropiate perechi de puncte dintr-un spațiu metric, date n puncte, astfel încât distanța dintre perechea de puncte să fie minimă.Algoritmul lui Strassen:Este un algoritm pentru multiplicarea matricei, care poartă numele de Volker Strassen. Sa dovedit a fi mult mai rapid decât algoritmul tradițional atunci când funcționează pe matrici mari.Algoritmul Cooley-Tukey Fast Fourier Transform (FFT):Algoritmul Fast Fourier Transform este numit după J. W. Cooley și John Turkey. Urmează abordarea Divide and Conquer și impune o complexitate de O(nlogn).Algoritmul Karatsuba pentru multiplicare rapidă:Este unul dintre cei mai rapidi algoritmi de înmulțire ai timpului tradițional, inventat de Anatoly Karatsuba la sfârșitul anului 1960 și publicat în 1962. Înmulțește astfel două numere de n cifre reducându-le la cel mult o singură cifră.

Avantajele Divide and Conquer

• Divide and Conquer tind să rezolve cu succes una dintre cele mai mari probleme, cum ar fi Turnul din Hanoi, un puzzle matematic. Este o provocare să rezolvi probleme complicate pentru care nu ai nicio idee de bază, dar cu ajutorul abordării împărți și cuceri, a redus efortul, deoarece lucrează la împărțirea problemei principale în două jumătăți și apoi le rezolvă recursiv. Acest algoritm este mult mai rapid decât alți algoritmi.
• Utilizează eficient memoria cache fără a ocupa mult spațiu, deoarece rezolvă subprobleme simple din memoria cache în loc să acceseze memoria principală mai lentă.
• Este mai priceput decât cel al lui omologul său tehnică Brute Force.
• Deoarece acești algoritmi inhibă paralelismul, acesta nu implică nicio modificare și este gestionat de sisteme care încorporează procesare paralelă.

Dezavantajele Divide and Conquer

• Deoarece majoritatea algoritmilor săi sunt proiectați prin încorporarea recursiunii, deci necesită un management ridicat al memoriei.
• O stivă explicită poate suprasolicita spațiul.
• Poate chiar să blocheze sistemul dacă recursiunea este efectuată cu mult mai mult decât stiva prezentă în CPU.