Știm o copac este o structură de date neliniară. Nu are limitare a numărului de copii. ACe este un arbore binar complet?

Un arbore binar complet este un tip special de arbore binar în care toate nivelurile arborelui sunt umplute complet, cu excepția nodurilor de cel mai jos nivel, care sunt umplute cât mai din stânga posibil.

Arborele binar complet

Câteva terminologii ale arborelui binar complet:

• Rădăcină – Nod în care nicio margine nu provine de la părinte. Exemplu -nodul A
• Copil – Nodul care are o margine de intrare se numește copil. Exemplu – nodurile B, F sunt copiii lui A și, respectiv, C.
• Frate – Nodurile care au același părinte sunt frați. Exemplul - D, E sunt frați, deoarece au același părinte B.
• Gradul unui nod – Numărul de copii ai unui anumit părinte. Exemplu: gradul A este 2 și gradul C este 1. Gradul D este 0.
• Noduri interne/externe – Nodurile frunză sunt noduri externe, iar nodurile care nu sunt frunze sunt noduri interne.
• Nivel – Numărați nodurile dintr-o cale pentru a ajunge la un nod de destinație. Exemplu - Nivelul nodului D este 2, deoarece nodurile A și B formează calea.
• Înălţime – Numărul de muchii pentru a ajunge la nodul destinație, Rădăcina este la înălțimea 0. Exemplu – Înălțimea nodului E este 2 deoarece are două muchii de la rădăcină.

Proprietățile arborelui binar complet:

• Se spune că un arbore binar complet este un arbore binar propriu, în care toate frunzele au aceeași adâncime.
• Într-un arbore binar complet, numărul de noduri la adâncime d este 2 ^d .
• Într-un arbore binar complet cu n înălțimea nodurilor arborelui este log(n+1) .
• Toate nivelurile cu excepția ultimului nivel sunt complet pline.

Arborele binar perfect vs Arborele binar complet:

Un arbore binar de înălțime „h” având numărul maxim de noduri este a perfect arbore binar.
Pentru o înălțime dată h , numărul maxim de noduri este 2 ^h+1 -1 .

A complet arbore binar de înălțime h este un arbore binar perfect până la înălțime h-1 , iar în ultimul nivel element sunt stocate în ordine de la stânga la dreapta.

Exemplul 1:

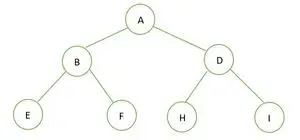
Un Arbore Binar

Înălțimea arborelui binar dat este 2 și numărul maxim de noduri din acel arbore este n= 2^h+1-1 = 2²⁺¹-1 = 2³-1 = 7 .
Prin urmare, putem concluziona că este un arbore binar perfect .
Acum, pentru un arbore binar complet, este plin până la înălțime h-1 adică; 1, iar elementele de ultimul nivel sunt stocate în ordine de la stânga la dreapta. Prin urmare, este și un arbore binar complet. Aici este reprezentarea elementelor atunci când sunt stocate într-o matrice

Element stocat într-o matrice nivel cu nivel

În matrice, toate elementele sunt stocate continuu.

Exemplul 2:

Sree Ramanujan

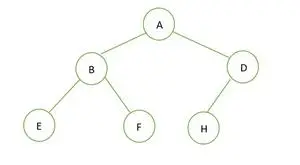
Un arbore binar

Înălțimea arborelui binar dat este 2, iar numărul maxim de noduri care ar trebui să existe sunt 2^h+1– 1 = 2²⁺¹– 1 = 2³– 1 = 7 .
Dar numărul de noduri din arbore este 6 . De aceea este nu un arbore binar perfect .
Acum, pentru un arbore binar complet, este plin până la înălțime h-1 adică; 1 , și ultimul element de nivel sunt stocate în ordine de la stânga la dreapta. Prin urmare, acesta este un arbore binar complet . Stocați elementul într-o matrice și va fi ca;

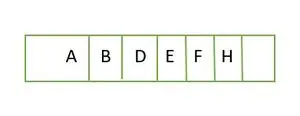
Element stocat într-o matrice nivel cu nivel

Exemplul 3:

variabile de tip java

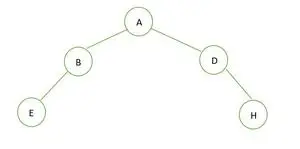
Un arbore binar

Înălțimea arborelui binar este de 2 și numărul maxim de noduri care pot fi acolo este de 7, dar există doar 5 noduri, de aceea este nu un arbore binar perfect .
În cazul unui arbore binar complet, vedem că în ultimul nivel elementele nu sunt completate de la stânga la dreapta. Deci este nu un arbore binar complet .

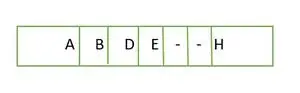
Element stocat într-o matrice nivel cu nivel

Elementele din matrice nu sunt continue.

Arborele binar complet vs Arborele binar complet:

Pentru un arbore binar complet, fiecare nod are fie 2 copii, fie 0 copii.

Exemplul 1:

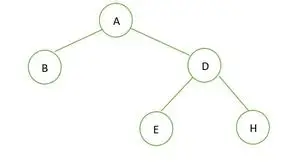
Un arbore binar

În arborele binar dat nu există niciun nod cu gradul 1, fie 2, fie 0 copii pentru fiecare nod, deci este un arbore binar complet .

Pentru un arbore binar complet, elementele sunt stocate nivel cu nivel și nu din partea stângă a ultimului nivel. Prin urmare, aceasta este nu un arbore binar complet . Reprezentarea matricei este:

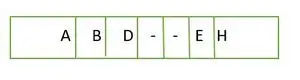
Element stocat într-o matrice nivel cu nivel

Exemplul 2:

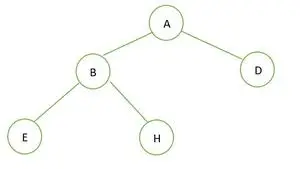
Un Arbore binar

În arborele binar dat nu există nici un nod cu gradul 1. Fiecare nod are un grad fie 2, fie 0. Prin urmare, este un arbore binar complet .

Pentru un arbore binar complet, elementele sunt stocate nivel cu nivel și completate din partea stângă a ultimului nivel. De aici aceasta a arbore binar complet . Mai jos este reprezentarea matrice a arborelui:

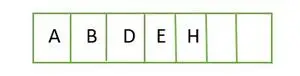
Element stocat într-o matrice nivel cu nivel

Exemplul 3:

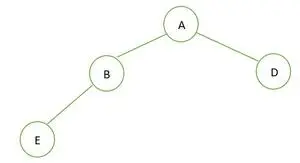
Un arbore binar

În arborele binar dat, nodul B are gradul 1, ceea ce încalcă proprietatea arborelui binar complet, deci este nu un arbore binar complet

algoritmul k-nn

Pentru un arbore binar complet, elementele sunt stocate nivel cu nivel și umplute din partea stângă a ultimului nivel. Prin urmare, acesta este un arbore binar complet . Reprezentarea matrice a arborelui binar este:

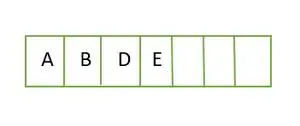
Element stocat într-o matrice nivel cu nivel

Exemplul 4:

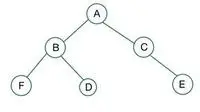
un arbore binar

d flip flop

În arborele binar dat, nodul C are gradul 1 care încalcă proprietatea unui arbore binar complet, deci este nu un arbore binar complet

Pentru un arbore binar complet, elementele sunt stocate nivel cu nivel și umplute din partea stângă a ultimului nivel. Aici nodul E încalcă condiția. Prin urmare, aceasta este nu un arbore binar complet .

Crearea arborelui binar complet:

Știm o arbore binar complet este un arbore în care, cu excepția ultimului nivel (să zicem l )tot celălalt nivel are ( 2l ) nodurile și nodurile sunt aliniate de la stânga la dreapta.
Poate fi reprezentat folosind o matrice. Dacă părintele este index i deci copilul stâng este la 2i+1 iar copilul potrivit este la 2i+2 .

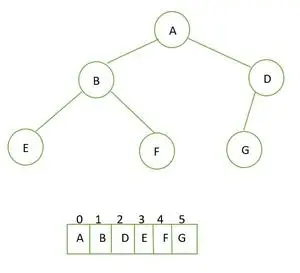
Arborele binar complet și reprezentarea sa matrice

Algoritm:

Pentru crearea unui Arborele binar complet , avem nevoie de a Pasul 1: Inițializați rădăcina cu un nou nod când arborele este gol.

Pasul 2: Dacă arborele nu este gol, atunci obțineți elementul frontal

• Dacă elementul frontal nu are un copil stâng, atunci setați copilul din stânga la un nou nod
• Dacă copilul potrivit nu este prezent, setați copilul potrivit ca nod nou

Pasul 3: Dacă nodul are ambii copii atunci pop e din coadă.

Pasul 4: Puneți noile date în coadă.

Ilustrare:

Luați în considerare matricea de mai jos:

actor chiranjeevi

1. Primul element va fi rădăcina (valoarea la index = 0 )

A este luat ca rădăcină

2. Următorul element (la index = 1 ) va fi stânga și al treilea element (index = 2 ) va fi copilul drept al rădăcinii

B ca copil stâng și D ca copil drept

3. al patrulea (indice = 3 ) și al cincilea element (index = 4 ) va fi copilul stâng și drept al nodului B

E și F sunt copii din stânga și din dreapta lui B

4. Următorul element (index = 5 ) va rămâne fiul nodului D

G este făcut fiul stâng al nodului D

Acesta este modul în care este creat un arbore binar complet.

Implementare: Pentru implementarea construirii unui Arbore Binar Complet din ordinea nivelului este dată în acest post .

Aplicarea arborelui binar complet:

• Sortare grămadă
• Structura de date bazată pe sortare heap

Verificați dacă un arbore binar dat este complet sau nu: Urma acest post pentru a verifica dacă arborele binar dat este complet sau nu.