Probabilitatea cărților este probabilitatea evenimentelor care implică un pachet de cărți de joc. După cum știm, probabilitatea este unul dintre subiectele importante ale matematicii care se ocupă de calculul posibilității oricărui eveniment. Cu cuvinte simple, probabilitatea cărților este o parte a probabilității în care găsim probabilitatea de a extrage o carte din pachetul de cărți. În acest articol, vom afla despre probabilitatea cărților cu toate detaliile despre diagrama probabilității cărților, probabilitatea cărților de joc, cum să găsim probabilitatea cărților și exemple rezolvate de probabilitatea cărților. Să începem învățarea pe tema probabilității cardurilor.
Ce este probabilitatea?
Probabilitatea este ramura matematicii care studiază posibilitățile ca orice eveniment să se întâmple sau nu. Din punct de vedere matematic, nu este altceva decât raportul dintre numărul de rezultate favorabile și numărul total de rezultate (spațiu eșantion) pentru un eveniment.
Câteva dintre exemplele din viața reală de probabilitate sunt:
- Jocuri de cărți, pentru a afla probabilitatea de a câștiga sau pierde jocul.
- Prognoza meteo, pentru a prezice ploaia.
- Rezultatele alegerilor, pentru a determina dacă candidatul va câștiga sau va pierde.
- Rezultatele examenului, pentru a identifica dacă candidatul va promova sau nu.
Formula probabilității
Dacă E este un eveniment cu spațiul eșantion S și numărul de rezultate favorabile este n(E), atunci probabilitatea evenimentului E și anume, P(E) este dată de:
P(E) = n(E) / n(S)
Ce este probabilitatea cardului?
Probabilitatea de a extrage o carte sau o colecție de cărți dintr-un pachet se numește Probabilitatea cărților. În cuvinte simple, probabilitatea legată de cărțile de joc se numește probabilitate de cărți. Deoarece acesta este tipul de probabilitate, se află întotdeauna între 0 și 1. De exemplu, dacă trebuie să găsim probabilitatea de a extrage un as din pachetul de cărți, adică 4/52 = 1/13 [Deoarece sunt 4 ași în pachetul de 52 de cărți].
Pachetul de cărți în probabilitate
Deck of Cards este o colecție de 52 de cărți care par să existe de mii de ani. Setul de cărți sau cărțile de joc sunt considerate a fi originare fie din India, fie din China, prima dovadă documentată a acestor cărți se găsește în 9.th-China secolului în timpul dinastiei Tang. Aceste cărți erau similare cărților din zilele noastre și, de asemenea, s-au împărțit în patru culori, dar numele și simbolul acelor costume sunt diferite, adică monede, șiruri de monede, miriade și miriade de zeci.
În zilele noastre, aceste cărți vin în diferite modele și sunt împărțite în patru culori și anume Spade (♠), Club (♣), Heart (❤) și Diamond (◆). Pentru o singură carte aleasă, spațiul eșantion este 52, adică numărul total de rezultate pentru o singură carte aleasă dintr-un pachet este 52.
n(S) pentru pachetul de cărți = 52
Tipuri de cărți dintr-un pachet
Orice pachet de cărți poate fi clasificat în mai multe moduri, unii dintre parametrii pe care pot fi clasificate cărțile sunt:
- Bazat pe Culori
- Bazat pe costume
Să înțelegem această clasificare în detaliu, după cum urmează:
Bazat pe Culori
Pe baza culorilor, un pachet de cărți poate fi clasificat în două categorii,
- Cartonașe roșii
- Cărți negre
Un total de 52 de cărți sunt împărțite în mod egal în cărți roșii și negre, ceea ce înseamnă că există 26 cărți roșii și 26 cărți negre în pachet.
Bazat pe costume
Există patru culori în pachetul de cărți care sunt:
- Inimi (❤)
- Diamante (◆)
- Cluburi (♣)
- pică (♠)
În afară de acestea, există încă o clasificare a cărților, bazată pe rangul cărților:
- As
- Carduri cu numere
- Cărți de față
As
Asul este o astfel de carte care fie este cea mai importantă, fie cea mai puțin importantă în funcție de joc. Această carte A scrisă pe ea și fiecare culoare are una dintre aceste cărți, adică patru cărți de as.
Carduri cu numere
De la 2 la 10, există 9 cărți per costum, astfel încât există un total de 36 de astfel de cărți.
Cărți de față
Cărțile cu față, după cum sugerează și numele, conțin o figură sau o față a figurii de pe card. Există trei cărți din fiecare culoare, adică Jack, Queen, King. Astfel, există un total de 12 cărți de față.
Toate aceste clasificări pot fi văzute în tabelul următor.
| pachet de cărți (52 de cărți) | ||||
|---|---|---|---|---|
| Carduri colorate | Carti negre (26 de carti) | Cartonașe roșii (26 de cărți) | ||
| Costume | Spade (13 cărți) | Club (13 cărți) | Inima (13 cărți) | Diamant (13 cărți) |
| Cărți de față (12 cărți într-un pachet și 3 cărți în fiecare culoare) | K (regele) | K (regele) | K (regele) | K (regele) |
| Q (regina) | Q (regina) | Q (regina) | Q (regina) | |
| J (Jack) | J (Jack) | J (Jack) | J (Jack) | |
| Carduri cu numere (36 de cărți într-un pachet și 9 cărți într-un costum) | 10 | 10 | 10 | 10 |
| 9 | 9 | 9 | 9 | |
| 8 | 8 | 8 | 8 | |
| 7 | 7 | 7 | 7 | |
| 6 | 6 | 6 | 6 | |
| 5 | 5 | 5 | 5 | |
| 4 | 4 | 4 | 4 | |
| 3 | 3 | 3 | 3 | |
| 2 | 2 | 2 | 2 | |
| Cărți de as (4 cărți în pachet și 1 carte într-un costum) | A (As) | A (As) | A (As) | A (As) |
Diagrama pachetului de cărți
Următorul grafic reprezintă clasificarea pachetului de cărți de joc:
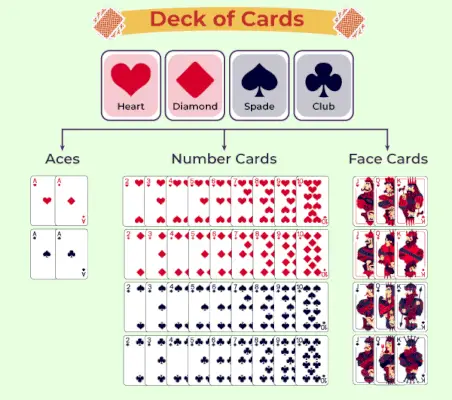
Probabilitatea cărților de joc
Unele dintre evenimentele comune în probabilitățile cardului sunt discutate în următorul tabel:
| Evenimentul E pentru cartea de desen | Probabilitate P(E) |
|---|---|
| Un As | P(E) = 4 / 52 = 1 / 13 |
| Un rege | P(E) = 4 / 52 = 1 / 13 |
| Un card cu numere | P(E) = 36 / 52 = 9 / 13 |
| O carte de față | P(E) = 12 / 52 = 3 / 13 |
| O carte de pică | P(E) = 13 / 52 = 1 / 4 |
| Un cartonaș roșu | P(E) = 26 / 52 = 1 / 2 |
Cum să găsiți probabilitatea cărților?
Pașii pentru a găsi probabilitatea evenimentelor care implică cărți sunt aceiași cu toate celelalte probabilități, care sunt date după cum urmează:
ls comandă Linux
Pasul 1: Mai întâi, găsiți numărul de rezultate favorabile de la întrebarea dată.
Pasul 2: Apoi, găsiți numărul total de rezultate.
Pasul 3: Aplicați formula probabilității pentru a găsi probabilitatea cardului.
Exemplu: Care este probabilitatea de a extrage un as dintr-un pachet de cărți?
Răspuns:
Aici, E este evenimentul de extragere a unei cărți de as
Numărul total de rezultate într-un pachet n(S) = 52
Numărul de rezultate favorabile = n(E) = extragerea unei cărți as din pachet = 4 (Există 4 cărți as într-un pachet)
P(E) = n(E) / n(S) = 4 / 52
P(E) = 1 / 13
Probabilitatea de a extrage o carte as = 1 / 13
Exemple de întrebări despre probabilitatea cardului
Problema 1: Care este probabilitatea de a extrage următoarele cărți dintr-un pachet de cărți?
(i) o pică
(ii) un cartonaș negru
(iii) un card cu număr
Soluţie:
(i) Aici, E este evenimentul de extragere a unei cărți de pică
Numărul total de rezultate într-un pachet n(S) = 52
Numărul de rezultate favorabile = n(E) = extragerea unei cărți de pică din pachet = 13 (Există 13 cărți de fiecare culoare într-un pachet)
P(E) = n(E) / n(S) = 13 / 52
P(E) = 1 / 4
Probabilitatea de a trage o pică = 1 / 4
(ii) Aici, E este evenimentul de a extrage o carte neagră
Numărul total de rezultate într-un pachet n(S) = 52
Numărul de rezultate favorabile = n(E) = extragerea unei cărți negre din pachet = 26 (Există 26 de cărți negre într-un pachet)
P(E) = n(E) / n(S) = 26 / 52
P(E) = 1 / 2
Probabilitatea de a extrage o carte neagră = 1 / 2
(iii) Aici, E este evenimentul de extragere a unei cărți cu număr
Numărul total de rezultate într-un pachet n(S) = 52
Numărul de rezultate favorabile = n(E) = extragerea unei cărți cu numere din pachet = 36 (Există 36 cărți cu numere într-un pachet)
P(E) = n(E) / n(S) = 36 / 52
P(E) = 9 / 13
Probabilitatea de a extrage o carte cu numere = 9 / 13
Problema 2: Care este probabilitatea de a extrage următoarele cărți dintr-un pachet de cărți?
(i) Un rege sau o carte neagră
(ii) Un cartonaș roșu și as
Soluţie:
(i) Aici, E este evenimentul de a extrage un rege sau o carte neagră
Numărul total de rezultate într-un pachet n(S) = 52
Numărul de rezultate favorabile = n(E) = extragerea unui rege sau a unei cărți negre din pachet = 26 + 2 = 28 (Există 26 de cărți negre în care 2 sunt rege și rămân 2 regi al negru într-un singur pachet)
P(E) = n(E) / n(S) = 28 / 52
P(E) = 7 / 13
Probabilitatea de a extrage un rege sau o carte neagră = 7/13
(ii) Aici, E este evenimentul de extragere a unei cărți roșii și as
Numărul total de rezultate într-un pachet n(S) = 52
Numărul de rezultate favorabile = n(E) = extragerea unei cărți roșii și as din pachet = 2 (Există 26 cărți roșii în care 2 sunt cărți as)
Conform întrebării, cartea extrasă ar trebui să fie roșie și as ambele. Prin urmare, n(E) = 2
P(E) = n(E) / n(S) = 2 / 52
P(E) = 1/26
Probabilitatea de a extrage o carte roșie și as = 1 / 26
Problema 3: Care este probabilitatea de a extrage următoarele cărți dintr-un pachet de cărți?
(i) Un card non-club
(ii) O carte fără față
Soluţie:
(i) Aici, E este evenimentul de extragere a unui card non-club
Numărul total de rezultate într-un pachet n(S) = 52
Numărul de rezultate favorabile = n(E) = extragerea unei cărți non-club din pachet = 39 (Există 13 cluburi într-un pachet, non-pack = 52 – 13 = 39)
P(E) = n(E) / n(S) = 39 / 52
P(E) = 3 / 4
Probabilitatea de a extrage un cartonaș non-club = 3 / 4
(ii) Aici, E este evenimentul de extragere a unei cărți fără față
Numărul total de rezultate într-un pachet n(S) = 52
Numărul de rezultate favorabile = n(E) = extragerea unei cărți fără față din pachet = 40 (Există 12 cărți cu față într-un pachet, fără pachet = 52 – 12 = 40)
P(E) = n(E) / n(S) = 40 / 52
P(E) = 10 / 13
Probabilitatea de a extrage un cartonaș non-club = 10 / 13
Problema 4: Care este probabilitatea de a extrage un cartonaș care nu este nici roșu, nici cartonaș?
Soluţie:
Aici, E este evenimentul de a extrage o carte nici roșie, nici cu fața
Numărul total de rezultate într-un pachet n(S) = 52
Numărul de rezultate favorabile = n(E) = nu extrage nici o carte roșie, nici o carte din pachet.
Total cartonașe roșii = 26
Există un total de 12 cărți de față într-un pachet, dar 6 cărți roșii sunt deja eliminate. Deci cărțile rămase = 12 – 6 = 6
n(E) = 26 + 6 = 32
P(E) = n(E) / n(S) = 32/ 52
P(E) = 8 / 13
Probabilitatea de a extrage o carte nici roșie, nici cu fața = 8 / 13
Problema 5: Care este probabilitatea de a extrage două cărți dintr-un pachet de cărți cu înlocuire atunci când prima carte este inimă și a doua carte este diamant?
Soluţie:
Probabilitatea de a extrage prima carte ca inimă = 13 / 52
După extragerea primei cărți, cartea este scoasă.
Probabilitatea de a extrage a doua carte ca un diamant = 13 / 51
Probabilitatea de a extrage prima carte ca inimă și a doua ca diamant = (13 / 52) × (13 / 51)
Probabilitatea de a extrage prima carte ca inimă și a doua ca diamant = 13 / 204
Întrebări frecvente despre probabilitatea cardului
1. Ce este probabilitatea cardului?
Probabilitatea de a extrage o carte din pachetul de cărți se numește probabilitate de cărți.
2. Enumerați tipurile de costume dintr-un pachet de cărți.
Există patru tipuri de costume într-un pachet de cărți. Sunt:
- Inimi
- Diamante
- Pică
- Cluburi
3. Care este spațiul eșantion pentru pachetul de cărți atunci când o carte este extrasă din pachet?
Eșantionul de spațiu pentru pachetul de cărți atunci când este extrasă o carte conține 52 de rezultate.
4. Scrieți formula pentru găsirea probabilității.
Formula pentru găsirea probabilității este dată de:
Probabilitatea evenimentului = Numărul de evenimente favorabile / Numărul total de rezultate
SAU
metode string în javaP(E) = n(E) / n(S)
5. Câte cărți de față sunt prezente într-un pachet de cărți?
Există 12 cărți de față prezente într-un pachet de cărți.
