Unghiul dintre doi vectori este unghiul dintre cozile lor și acest unghi poate fi găsit ușor folosind produsul încrucișat și produsul punctual al formulelor vectoriale. Unghiul dintre doi vectori este întotdeauna între 0° și 180°.
În acest articol vom afla în detaliu despre unghiul dintre doi vectori, definiție, formule și exemple.
Care este unghiul dintre doi vectori?
Unghiul dintre doi vectori este unghiul format la intersecția cozilor lor. Unghiul dintre doi vectori poate fi acut, drept sau obtuz, în funcție de direcția vectorilor.
Unghiul dintre doi vectori este găsit folosind două formule:
- Utilizarea produsului punctual al vectorilor
- Utilizarea produsului încrucișat al vectorilor
Acest lucru este explicat în formula de mai jos.
Unghiul dintre doi vectori formule
Unghiul dintre doi vectori este ușor și cel mai frecvent găsit folosind produsul scalar al vectorilor.

Doi vectori A și B
Produs punctual a lui A și B este dat de,
vec{A}.vec{B} = |A| |B| cosθ.
Cazuri speciale
- Când unghiul dintre vectori este de 0 grade.
Adică θ = 0°
⇒ |A| |B| cosθ
⇒ |A| |B| cos0°
⇒ |A| |B| [cos0° = 1]
- Când unghiul dintre vectori este de 180 de grade.
⇒ |A| |B| cosθ
⇒ |A| |B| cos180°
⇒ – |A| |B| [cos180° = -1]
- Când unghiul dintre vectori este de 90 de grade.
⇒ |A| |B| cosθ
⇒ |A| |B| cos90°
⇒ |A| |B| × 0 [cos90° = 0]
⇒ 0
Formula pentru unghiul dintre doi vectori
Cosinusul unghiului dintre doi vectori este egal cu suma produsului constituenților individuali ai celor doi vectori, împărțit la produsul mărimii celor doi vectori.
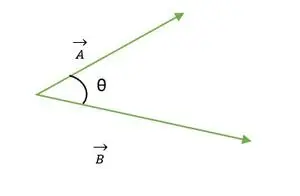
Doi vectori A și B
cosθ=
θ= cos-1
În formă carteziană,
A = AXi + Așij + ACuk
B= BXi + Bșij + BCuk
cos θ =
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}
Proprietățile produsului Dot
- Produsul punctual este comutativ
vec{A}.vec{B}=vec{B}.vec{A}
- Produsul punct este distributiv
vec{A}.(vec{B}+vec{C})=(vec{A}.vec{B}+vec{A}.vec{C})
Unghiul dintre doi vectori este cuprins între 0 ≤ θ ≤ 180. Când cozile sau capetele ambilor vectori coincid, atunci se calculează unghiul dintre vectori.
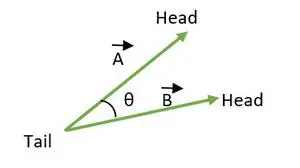
Coada coincide
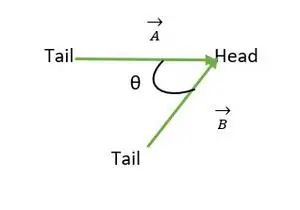
Capul coincide
Exemple de probleme Unghiul dintre doi vectori Formula
Problema 1: Aflați unghiul dintre vectori (dacă formează un triunghi echilateral)
- vectori a și b
- vectorii b și c
- vectori a și c
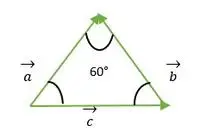
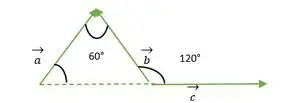
Triunghi echilateral format din vectorul a, b, c
Soluţie:
- vectori a și b
Pentru vectorul a și b, capul ambilor vectori coincide unul cu celălalt, prin urmare unghiul dintre vectorul a și b este același cu unghiul dintre două laturi ale triunghiului echilateral = 60°.
- vectorii b și c:
Din figura de mai sus, vedem că capul sau coada vectorului b și c nu coincid unul cu celălalt.
Deci, prin utilizarea proprietății- Un vector rămâne neschimbat dacă este transmis paralel cu el însuși.
Vectorul c este deplasat paralel cu el însuși
Acum vedem coada vectorilor b și c coincid între ele, prin urmare este aceeași cu unghiul exterior făcut cu un triunghi echilateral = 120°.
- vectori a și c
Coada lui a și c coincid
Pentru vectorii a și c, coada ambilor vectori coincid unul cu celălalt, prin urmare unghiul dintre vectorul a și c este același cu unghiul dintre două laturi ale triunghiului echilateral = 60°.
Problema 2: Găsiți unghiuri între vectori dacă formează un triunghi dreptunghic isoscel.
- vectorul a și b
- vectorul b și c
- vectori a și c
Soluţie:
- vectorul a și b
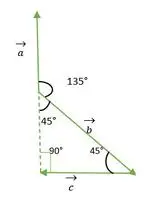
Triunghi isoscel cu unghi drept
Din figura de mai sus, vedem că capul sau coada vectorului a și b nu coincid unul cu celălalt. Deci, prin utilizarea proprietății- Un vector rămâne neschimbat dacă este transmis paralel cu el însuși.
un vector este deplasat paralel cu el însuși
Acum, cozile vectorilor a și b coincid între ele și formează un unghi la fel ca unghiul exterior al unui triunghi isoscel drept unghi = 135°.
- vectorul b și c
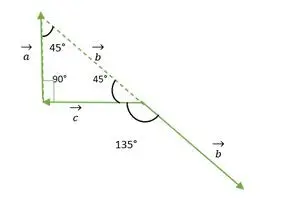
Triunghi isoscel cu unghi drept
Din figura de mai sus, capul sau cozile vectorului b și c nu coincid unul cu celălalt. Deci, prin utilizarea proprietății, un vector rămâne neschimbat dacă este transmis paralel cu el însuși.
vectorul b este deplasat paralel cu el însuși
Acum, cozile vectorilor b și c coincid între ele și formează un unghi la fel ca unghiul exterior al unui triunghi isoscel cu unghi drept = 135°.
- vectori a și c
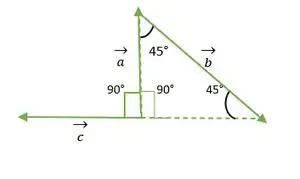
Triunghi isoscel cu unghi drept
Din figura de mai sus, capul sau cozile vectorului a și c nu coincid unul cu celălalt. Deci, prin utilizarea proprietății- Un vector rămâne neschimbat dacă este transmis paralel cu el însuși.
vectorul c este mutat paralel cu el însuși
Acum, cozile vectorilor a și c coincid între ele și formează un unghi la fel ca unghiul drept al triunghiului isoscel = 90°.
Problema 3: Aflați unghiul dintre vectorii A = i + j + k și vectorul B = -2i – 2j – 2k.
Soluţie:
Din formula,
A = AXi + Așij + ACuk
B= BXi + Bșij + BCuk
cosθ=
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})} Aici, în întrebarea dată,
A= i + j + k
B= -2i -2j -2k
Înlocuirea valorilor din formulă
⇒ cosθ =
frac{(1.(-2)+1.(-2)+1.(-2))}{(sqrt{1^2+1^2+1^2}×sqrt{(-2)^2+(-2)^2+(-2)^2})} ⇒ cosθ =
frac{(-2-2-2)}{(sqrt{1+1+1}×sqrt{4+4+4})} ⇒ cosθ =
frac{-6}{(sqrt{3}×sqrt{12})} ⇒ cosθ =
frac{-6}{(sqrt{36})} ⇒ cosθ = -6/6
⇒ cosθ= -1
⇒ θ = 180°
Problema 4: Aflați unghiul dintre vectorul A = 3i + 4j și B = 2i + j
Soluţie:
A = AXi + Așij + ACuk
B = BXi + Bșij + BCuk
cosθ =
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})} Dat aici,
A= 3i + 4j + 0k
B= 2i + j + 0k
Inlocuind valorile din formula,
⇒ cosθ =
frac{(3.2+4.1+0.0)}{(sqrt{3^2+4^2+0^2}×sqrt{2^2+1^2+0^2})} ⇒ cosθ =
frac{(6+4+0)}{(sqrt{9+16+0}×sqrt{4+1+0})} ⇒ cosθ =
frac{(10)}{(sqrt{25}×sqrt{5})} ⇒ cosθ =
frac{(10)}{(sqrt{125})} ⇒ θ = cos-1(
frac{(10)}{5.(sqrt{5})} )⇒ θ = cos-1(
frac{2}{(sqrt{5})} )care este 10 din 60
Problema 5: Aflați unghiul dintre vectorul A = i + j și Vector B = j + k.
Soluţie:
Din formula,
A = AXi + Așij + ACuk
B = BXi + Bșij + BCuk
cosθ =
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})} Aici, în întrebarea dată,
⇒ A = i + j
⇒ B = j + k
⇒ cosθ =
frac{(1.0+1.1+0.1)}{(sqrt{1^2+1^2+0^2}×sqrt{0^2+1^2+1^2})} ⇒ cosθ =
frac{(1)}{(sqrt{1+1+0}×sqrt{0+1+1})} ⇒ cosθ =
frac{1}{(sqrt{2}×sqrt{2})} ⇒ θ = cos-1(1/2)
⇒ θ = 60°