SCORUL Z ÎN STATISTICI - ȘTIINȚA DATELOR

Scorul Z în statistici este o măsurare a câte abateri standard este un punct de date față de media unei distribuții. Să găsim scorul z în statistici. Un scor z de 0 indică faptul că scorul punctului de date este același cu scorul mediu. Un scor z pozitiv indică faptul că punctul de date este peste medie, în timp ce un scor z negativ indică faptul că punctul de date este sub medie.

Formula pentru calcularea unui scor z este: z = (x – μ)/ p

Unde:

concat șir java

X: este valoarea de test
m: este media
la: este valoarea standard

În acest articol, vom discuta următoarele concepte:

Cuprins

Ce este Z-Score?
Cum se calculează scorul Z?
Caracteristicile Z-Score
Calculați valori aberante utilizând valoarea scorului Z
Implementarea Z-Score în Python
Aplicarea Z-Score
Scoruri Z vs. Deviația standard
De ce scorurile Z sunt numite scoruri standard?

Ce este Z-Score?

Scorul Z, cunoscut și sub denumirea de scor standard, ne indică abaterea unui punct de date de la medie, exprimându-l în termeni de abateri standard deasupra sau sub medie. Ne oferă o idee despre cât de departe este un punct de date de medie. Prin urmare, scorul Z este măsurat în termeni de abatere standard de la medie. De exemplu, un scor Z de 2 indică faptul că valoarea este la 2 abateri standard de la medie. Pentru a folosi un scor z, trebuie să cunoaștem media populației (μ) și, de asemenea, abaterea standard a populației (σ).

Formula pentru scorul Z

Un scor z poate fi calculat folosind următoarea formulă.

z = (X – μ) / p

Unde,

z = Scorul Z
X = Valoarea elementului
μ = Media populației
σ = Abaterea standard a populației

Cum se calculează scorul Z?

Ni se oferă media populației (μ), abaterea standard a populației (σ) și valoarea observată (x) în enunțul problemei, înlocuind aceeași în ecuația scorului Z, ne dă valoarea scorului Z. În funcție de dacă scorul Z dat este pozitiv sau negativ, putem folosi Tabel Z pozitiv sau Tabel Z negativ disponibil online sau pe spatele manualului de statistică din anexă.

Exemplul 1:

Susți examenul GATE și obții 500. Scorul mediu pentru GATE este 390, iar abaterea standard este 45. Cât de bine ai obținut un punctaj la test în comparație cu examinatorul mediu?

Soluţie:

Următoarele date sunt ușor disponibile în declarația de întrebare de mai sus

Scorul brut/valoarea observată = X = 500

Scorul mediu = μ = 390

Abaterea standard = σ = 45

Prin aplicarea formulei scorului z,

z = (X – μ) / p

z = (500 – 390) / 45

z = 110 / 45 = 2,44

Aceasta înseamnă că scorul tău z este 2.44 .

Deoarece scorul Z este pozitiv 2,44, vom folosi tabelul Z pozitiv.

ciclul de viață al dezvoltării software

Acum să aruncăm o privire la Tabelul Z (CC-BY) pentru a ști cât de bine ați obținut scoruri în comparație cu ceilalți examinați.

Urmați instrucțiunile de mai jos pentru a găsi probabilitatea din tabel.

Aici, scorul z = 2,44, care i indică faptul că punctul de date este cu 2,44 deviații standard peste medie.

În primul rând, mapați primele două cifre 2.4 pe axa Y.
Apoi de-a lungul axei X, harta 0,04
Uniți ambele axe. Intersecția celor două vă va oferi probabilitatea cumulativă asociată cu valoarea scorului Z pe care o căutați

[Această probabilitate reprezintă aria de sub curba normală standard din stânga scorului Z]

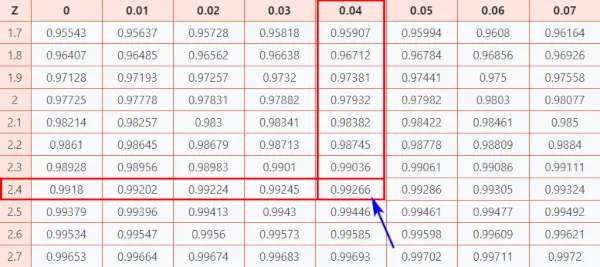
Tabel de distribuție normală

Ca rezultat, veți obține valoarea finală care este 0,99266 .

Acum, trebuie să comparăm modul în care scorul nostru original de 500 la examenul GATE se compară cu scorul mediu al lotului. Pentru a face acest lucru, trebuie să convertim probabilitatea cumulativă asociată cu scorul Z într-o valoare procentuală.

0,99266 × 100 = 99,266%

În cele din urmă, puteți spune că ați făcut bine decât aproape 99% a altor examinatori.

Exemplul 2 : Care este probabilitatea ca un elev să obțină un punctaj între 350 și 400 (cu un scor mediu μ de 390 și o abatere standard σ de 45)?

Soluţie:

Scorul minim = X₁= 350

Scorul maxim = X₂= 400

Prin aplicarea formulei scorului z,

Cu₁= (X1 – m) / p

Cu₁= (350 – 390) / 45

Cu₁= -40 / 45 = -0,88

Cu₂= (X₂– m) / p

z2 = (400 – 390) / 45

Cu₂= 10 / 45 = 0,22

Deoarece z1 este negativ, va trebui să ne uităm la un negativ Masa Z și găsiți că probabilitatea cumulativă p1, prima probabilitate, este 0,18943 .

Cu₂este pozitivă, deci folosim un Z-Tabel pozitiv care dă o probabilitate cumulativă p₂de 0,58706 .
programare cobol

Probabilitatea finală se calculează scăzând p1 din p₂:

p = p₂– p₁

p = 0,58706 – 0,18943 = 0,39763

Probabilitatea ca un student să obțină scoruri între 350 și 400 este 39,763% (0,39763 * 100).

Caracteristicile Z-Score

Mărimea scorului Z reflectă cât de departe este un punct de date de medie în termeni de abateri standard.
Un element care are un scor z mai mic de 0 înseamnă că elementul este mai mic decât media.
Scorurile Z permit compararea punctelor de date din diferite distribuții.
Un element având un scor z mai mare decât 0 înseamnă că elementul este mai mare decât media.
Un element având un scor z egal cu 0 reprezintă faptul că elementul este egal cu media.
Un element având un scor z egal cu 1 reprezintă faptul că elementul este cu 1 abatere standard mai mare decât media; un scor z egal cu 2, 2 abateri standard mai mari decât media și așa mai departe.
Un element având un scor z egal cu -1 reprezintă faptul că elementul este cu 1 abatere standard mai mică decât media; un scor z egal cu -2, cu 2 abateri standard mai mici decât media și așa mai departe.
Dacă numărul de elemente dintr-o mulțime dată este mare, atunci aproximativ 68% dintre elemente au un scor z între -1 și 1; aproximativ 95% au un scor z între -2 și 2; aproximativ 99% au un scor z între -3 și 3. Aceasta este cunoscută sub numele de Regula Empirică și precizează procentul de date în anumite abateri standard de la medie într-o distribuție normală, așa cum este demonstrat în imaginea de mai jos.

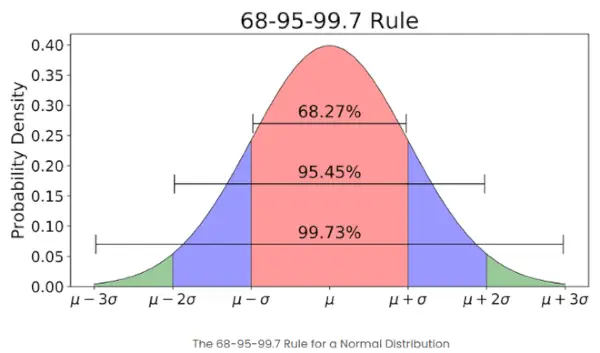
Regula empirică în distribuția normală

Calculați valori aberante utilizând valoarea scorului Z

Putem calcula valori aberante în date folosind valoarea scorului z a punctelor de date. Pașii pentru a lua în considerare un punct de date abere sunt următorii:

La început, adunăm setul de date în care dorim să vedem valorile aberante
Vom calcula media și abaterea standard a setului de date. Aceste valori vor fi utilizate pentru a calcula valoarea z-score a fiecărui punct de date.
Vom calcula valoarea scorului z pentru fiecare punct de date. Formula pentru calcularea valorii scorului z va fi aceeași ca
Z = frac{{X – mu}}{{sigma}}
unde X va fi punctul de date, μ este media datelor și σ este abaterea standard a setului de date.
Vom determina valoarea limită pentru scorul z după care punctul de date ar putea fi considerat un valori abere. Această valoare limită este un hiperparametru pe care îl decidem în funcție de proiectul nostru.
Un punct de date a cărui valoare z-score este mai mare de 3 înseamnă că punctul de date nu aparține punctului de 99,73 % al setului de date.
Orice punct de date al cărui z-score este mai mare decât valoarea limită hotărâtă de noi va fi considerat aberant.

Verifica: Scorul Z pentru detectarea valorii aberante

Implementarea Z-Score în Python

Putem folosi Python pentru a calcula valoarea z-score a punctelor de date din setul de date. De asemenea, vom folosi biblioteca numpy pentru a calcula media și abaterea standard a setului de date.

Python3

 import numpy as np def calculate_z_score(data): # Mean of the dataset mean = np.mean(data) # Standard Deviation of tha dataset std_dev = np.std(data) # Z-score of tha data points z_scores = (data - mean) / std_dev return z_scores # Example dataset dataset = [3,9, 23, 43,53, 4, 5,30, 35, 50, 70, 150, 6, 7, 8, 9, 10] z_scores = calculate_z_score(dataset) print('Z-Score :',z_scores) # Data points which lies outside 3 standard deviatioms are outliers # i.e outside range of99.73% values outliers = [data_point for data_point,  z_score in zip(dataset, z_scores) if z_score>3] print(f'
Valorile aberante din setul de date sunt {outliers}')>

Ieșire:

Scor Z : [-0,7574907 -0,59097335 -0,20243286 0,35262498 0,6301539 -0,72973781
-0,70198492 -0,00816262 0,13060185 0,54689523 1,10195307 3,32218443
-0,67423202 -0,64647913 -0,61872624 -0,59097335 -0,56322046]
Valorile aberante din setul de date sunt [150]

Aplicarea Z-Score

Scorurile Z sunt adesea folosite pentru scalarea caracteristicilor pentru a aduce diferite caracteristici la o scară comună. Funcțiile de normalizare asigură că acestea au varianță medie și unitate zero, ceea ce poate fi benefic pentru anumiți algoritmi de învățare automată, în special pentru cei care se bazează pe măsuri la distanță.
Scorurile Z pot fi folosite pentru a identifica valorile aberante dintr-un set de date. Punctele de date cu scoruri Z peste un anumit prag (de obicei 3 abateri standard de la medie) pot fi considerate valori aberante.
Scorurile Z pot fi utilizate în algoritmii de detectare a anomaliilor pentru a identifica cazurile care se abat semnificativ de la comportamentul așteptat.
Scorurile Z pot fi aplicate pentru a transforma distribuțiile distorsionate în distribuții mai normale.
Când se lucrează cu modele de regresie, scorurile Z ale reziduurilor pot fi analizate pentru a verifica homoscedasticitatea (varianța constantă a reziduurilor).
Scorurile Z pot fi utilizate în scalarea caracteristicilor analizând abaterile lor standard de la medie.

Scoruri Z vs. Deviația standard

Z- Scor	Deviație standard
Transformați datele brute într-o scară standardizată.	Măsoară cantitatea de variație sau dispersie într-un set de valori.
Ușurează compararea valorilor din diferite seturi de date, deoarece acestea elimină unitățile de măsură originale.	Deviația standard păstrează unitățile de măsură originale, ceea ce o face mai puțin potrivită pentru comparații directe între seturi de date cu unități diferite.
Indicați cât de departe este un punct de date de medie în termeni de abateri standard, oferind o măsură a poziției relative a punctului de date în cadrul distribuției sql selectează mai multe tabele	Exprimat în aceleași unități ca și datele originale, oferind o măsură absolută a modului de răspândire a valorilor în jurul mediei

Z- Scor

Deviație standard

Transformați datele brute într-o scară standardizată.

Măsoară cantitatea de variație sau dispersie într-un set de valori.

Ușurează compararea valorilor din diferite seturi de date, deoarece acestea elimină unitățile de măsură originale.

Deviația standard păstrează unitățile de măsură originale, ceea ce o face mai puțin potrivită pentru comparații directe între seturi de date cu unități diferite.

Indicați cât de departe este un punct de date de medie în termeni de abateri standard, oferind o măsură a poziției relative a punctului de date în cadrul distribuției

sql selectează mai multe tabele

Exprimat în aceleași unități ca și datele originale, oferind o măsură absolută a modului de răspândire a valorilor în jurul mediei

Verifica: Tabelul Z-Score

De ce scorurile Z sunt numite scoruri standard?

Scorurile Z sunt cunoscute și ca scoruri standard, deoarece standardizează valoarea unei variabile aleatoare. Aceasta înseamnă că lista de scoruri standardizate are o medie de 0 și o abatere standard de 1,0. Scorurile Z permit, de asemenea, compararea scorurilor pe diferite tipuri de variabile. Acest lucru se datorează faptului că folosesc starea relativă pentru a echivala scorurile de la diferite variabile sau distribuții.

Scorurile Z sunt folosite frecvent pentru a compara o variabilă cu o distribuție normală standard (cu μ = 0 și σ = 1).

Z-Score în statistici – Întrebări frecvente

Care este semnificația scorurilor Z pozitive și negative?

Scorurile Z pozitive indică valori peste medie, în timp ce scorurile Z negative indică valori sub medie. Semnul reflectă direcția abaterii de la medie.

Ce înseamnă un scor Z de 0?

Un scor Z de 0 indică faptul că valoarea punctului de date este exact la media setului de date. Aceasta sugerează că punctul de date nu este nici deasupra, nici sub medie.

Care este regula 68-95-99.7 în legătură cu scorurile Z?

Regula 68-95-99.7, cunoscută și sub numele de Regula empirică, afirmă că:

Aproximativ 68% dintre date se încadrează la o abatere standard de la medie.
Aproximativ 95% se încadrează în 2 abateri standard.
Aproximativ 99,7% se încadrează în 3 abateri standard.

Se pot folosi Z-Scores pentru distribuții non-normale?

Scorurile Z se bazează pe presupunerea că datele urmează o distribuție normală. Cu toate acestea, în practică, scorurile Z sunt benefice pentru datele care urmează o distribuție normală. În timp ce scorurile Z pot fi calculate pentru orice distribuție, interpretarea lor devine mai puțin fiabilă și mai simplă atunci când se ocupă de date nedistribuite în mod normal.

Cum pot fi aplicate Z-Scores în situații reale?

Z-Scores au diverse aplicații, cum ar fi în finanțe pentru analiza portofoliului, educație pentru testare standardizată, sănătate pentru evaluări clinice și multe altele. Acestea oferă o măsură standardizată pentru compararea și interpretarea datelor.