Volumul unei sfere este cantitatea de lichid pe care o poate conține o sferă. Formula volumului sferei este dată ca 4/3πr3. Este spațiul ocupat de o sferă în spațiul tridimensional. Se măsoară în unitate3eu sunt3, cm3, etc. O sferă este un obiect solid tridimensional cu o formă rotundă în geometrie.
Volumul sferei este spațiul total ocupat de suprafața sferei și este proporțional cu cubul razei sferei. În acest articol, vom afla despre volumul sferei, volumul formulei sferei, exemplele de formule ale volumului sferei și altele în detaliu.
Cuprins
- Ce este volumul unei sfere?
- Formula volumului sferei
- Volumul unei sfere solide
- Volumul unei sfere goale
- Volumul de derivare a formulei sferei
- Cum se calculează volumul sferei?
Ce este volumul unei sfere?
Volumul unei sfere este cantitatea de spațiu pe care o ocupă în interiorul acesteia. Sfera este o formă solidă rotundă tridimensională în care toate punctele de pe suprafața sa sunt distanțate egal de centrul său. Distanța fixă este raza sferei, iar punctul fix este centrul sferei. Vom observa o schimbare de formă atunci când cercul este întors. Ca urmare a rotației obiectului bidimensional cunoscut sub numele de cerc, se obține forma tridimensională a unei sfere.
Află mai multe,
- Sferă
- Suprafața sferei
Definiția volumului unei sfere
Volumul unei sfere este masa totală închisă de suprafața sferei. Este spațiul 3-D din interiorul sferei. Depinde de raza sferei. Imaginea adăugată mai jos arată o sferă cu raza r și volumul acesteia.
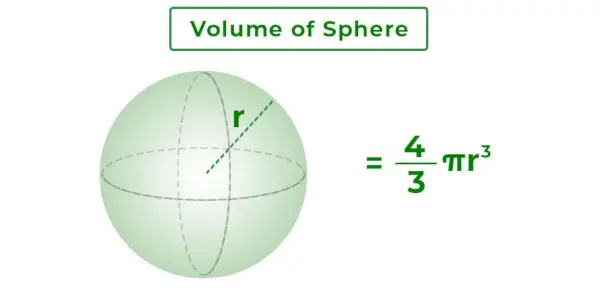
Formula volumului sferei
Formula volumului sferei este formula care este utilizată pentru a găsi volumul sferei atunci când este dată raza acesteia. Formula volumului sferei pentru sfera cu raza R este adăugată mai jos,
Formula volumului sferei = 4/3πr 3
Unde,
- r este raza unei sfere
- Pi este o constantă și valoarea sa este 22/7
O sferă este, în general, clasificată în două, care sunt,
- Volumul sferei solide
- Volumul sferei goale
Să învățăm despre ele în detaliu.
Volumul unei sfere solide
O sferă solidă este o sferă care este complet umplută până în interior. adică are masă până la miez și formula sa pentru volum atunci când raza sa este r este,
Volumul unei sfere solide (V) = (4/3)πr 3
Volumul unei sfere goale
Pentru o sferă goală, spațiul său interior este gol și să presupunem că raza sa exterioară este R iar raza sa interioară este r, apoi volumul său este calculat folosind formula,
Volumul sferei goale = (4/3)π(R 3 – r 3 )
Volumul de derivare a formulei sferei
Formula volumului sferei poate fi derivată folosind următoarele metode:
- Folosind integrarea
- Folosind Arhimede Relația dintre cilindru, con și sferă
Să discutăm aceste metode în detaliu, după cum urmează:
Volumul sferei utilizând integrarea
Folosind abordarea integrării, putem calcula pur și simplu volumul unei sfere.
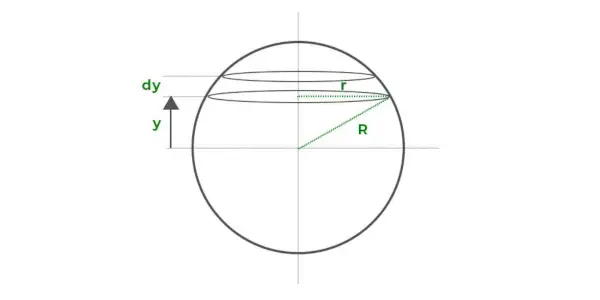
Să presupunem că volumul sferei este alcătuit dintr-o serie de discuri circulare subțiri stivuite unul peste altul, așa cum este desenat în diagrama de mai sus. Fiecare disc subțire are o rază de r și o grosime de dy care este distanța y față de axa x.
Lăsați volumul unui disc să fie dV. Valoarea dV este dată de,
dV = (πr2) tu
Astfel, dV = π (R2- și2) tu
Volumul total al sferei va fi suma volumelor tuturor acestor discuri mici. Valoarea cerută poate fi obținută prin integrarea expresiei de la limita -R la R.
Deci, volumul sferei devine,
V =
⇒ V =
⇒ V =
⇒ V =
⇒ V =
⇒ V =
Astfel, se obține formula pentru volumul sferei.
Volumul sferei folosind relațiile lui Arhimede
După cum a demonstrat deja Arhimede, dacă un con, o sferă și un cilindru au aceeași rază r și aceeași înălțime, volumele lor sunt în raport de 1:2:3.
Prin urmare putem spune:
Volumul cilindrului = Volumul conului + Volumul sferei
Astfel, volumul sferei = volumul cilindrului – volumul conului
După cum știm, acel volum al cilindrului = πr2h și volumul conului = (1/3)πr2h
Înlocuind aceste valori în ecuație, obținem:
Volumul sferei = πr2h – (1/3)πr2h = (2/3)πr2h
Presupunem că înălțimea cilindrului este egală cu diametrul sferei, care este 2r. Prin urmare:
Volumul sferei este (2/3)πr 2 h = (2/3)πr 2 (2r) = (4/3)πr 3
De asemenea, verifica
- Formula de volum a capacului sferic
- Formula sectorului sferic
- Formula segmentului sferic
Cum se calculează volumul sferei?
Volumul sferei este spațiul ocupat de o sferă. Volumul acestuia poate fi calculat folosind formula V = 4/3πr 3 .
Pașii necesari pentru a calcula volumul unei sfere sunt:
Pasul 1: Marcați valoarea razei sferei.
2 septembrie: Găsiți cubul razei.
Pasul 3: Înmulțiți cubul razei cu (4/3)π
Pasul 4: Adăugați (unitatea)3la răspunsul final.
Exemplu pentru a calcula volumul sferei
Exemplu: Aflați volumul unei sfere cu raza de 7 cm.
Având în vedere, r = 7 cm
V = (4/3)πr3
Volumul sferei, V = ((4/3) × π × 73) cm3
Inaltime = 1436,8 cm3
Astfel, volumul sferei este de 1436,8 cm3
Citeşte mai mult
- Volumul conului
- Volumul cubului
- Volumul cilindrului
Exemple de volum de sfere
Exemplul 1. Aflați volumul sferei a cărei rază este de 9 cm.
Soluţie:
Avem, r = 9
Volumul sferei = 4/3 πr3
⇒ Volumul sferei = (4/3) (3,14) (9) (9) (9)
⇒ Volumul sferei = (4) (3,14) (3) (9) (9)
⇒ Volumul sferei = 3052 cm3
Exemplul 2. Aflați volumul sferei a cărei rază este de 12 cm.
Soluţie:
Avem, r = 12
Volumul sferei = 4/3 πr3
⇒ Volumul sferei = (4/3) (3,14) (12) (12) (12)
⇒ Volumul sferei = (4) (3,14) (4) (12) (12)
⇒ Volumul sferei = 7234,56 cm3
Exemplul 3. Aflați volumul sferei a cărei rază este de 6 cm.
Soluţie:
Avem, r = 6
Volumul sferei = 4/3 πr3
⇒ Volumul sferei = (4/3) (3,14) (6) (6) (6)
⇒ Volumul sferei = (4) (3,14) (2) (6) (6)
⇒ Volumul sferei = 904,32 cm3
Exemplul 4. Aflați volumul sferei a cărei rază este de 4 cm.
Soluţie:
Avem, r = 4
Volumul sferei = 4/3 πr3
⇒ Volumul sferei = (4/3) (3,14) (4) (4) (4)
⇒ Volumul sferei = (1,33) (3,14) (4) (4) (4)
⇒ Volumul sferei = 267,27 cm3
Exemplul 5. Aflați volumul sferei al cărei diametru este de 10 cm.
Soluţie:
Avem, 2r = 10
listă sortată java⇒ r = 5
Volumul sferei = 4/3 πr3
⇒ Volumul sferei = (4/3) (3,14) (5) (5) (5)
⇒ Volumul sferei = (1,33) (3,14) (5) (5) (5)
⇒ Volumul sferei = 522,025 cm3
Exemplul 6. Aflați volumul sferei al cărei diametru este de 16 cm.
Soluţie:
Avem, 2r = 16
⇒ r = 8
Volumul sferei = 4/3 πr3
⇒ Volumul sferei = (4/3) (3,14) (8) (8) (8)
⇒ Volumul sferei = (1,33) (3,14) (8) (8) (8)
⇒ Volumul sferei = 2138,21 cm3
Exemplul 7. Aflați volumul sferei al cărei diametru este de 14 cm.
Soluţie:
Avem, 2r = 14
⇒ r = 7
Volumul sferei = 4/3 πr3
⇒ Volumul sferei = (4/3) (3,14) (7) (7) (7)
⇒ Volumul sferei = (1,33) (3,14) (7) (7) (7)
⇒ Volumul sferei = 1432,43 cm3
Volumul de întrebări sferă-practică
Î1: Aflați volumul sferei al cărei diametru este de 34 cm.
Î2: Aflați volumul sferei goale a cărei interior este de 4 cm și raza exterioară este de 8 cm.
Î3: Aflați volumul sferei a cărei rază este de 14 cm.
Î4: Care este volumul sferei a cărei rază este egală cu latura pătratului cu aria de 144 m2.
Volumul Sphere-Întrebări frecvente
Ce este volumul sferei?
Volumul sferei este spațiul ocupat de suprafața sferei.
Care este suprafața unei formule sfere?
Suprafața totală a sferei cu raza r este, Aria = 4πr 2
Care este formula pentru volumul unei sfere?
Volumul unei sfere cu raza r este, Volumul = 4/3πr 3
Cum găsim volumul emisferei?
Volumul unei emisfere cu raza r este, Volumul = 2/3πr 3
Care este raportul dintre volumul sferei și emisferei?
Dacă o sferă și o emisferă au aceleași raze, atunci raportul dintre volumul lor este:
ÎN 1 : IN 2 = (4/3πr 3 ): (2/3πr 3 ) = 2 : 1
Care este unitatea de volum a unei sfere?
Volumul sferei se măsoară în m3, cm3, litri etc. m 3 este unitatea de măsură standard.
Care este volumul sferei când raza sa este înjumătățită?
Volumul sferei = (4/3)πr3= (4/3)π(r/2)3= (4/3)π(r3/8) = Volumul/8. Deci volumul sferei devine o opteme.
