Suprafața unei prisme: În matematică, o prismă este un membru esențial al familiei poliedrelor și este definită ca o formă tridimensională având două poligoane identice față în față și care sunt conectate lateral prin fețe dreptunghiulare sau paralelograme. Poligoanele identice pot fi triunghiuri, pătrate, dreptunghiuri, pentagoane sau orice alt poligon cu n laturi și se numesc bazele prismei. Celelalte fețe ale unei prisme sunt paralelograme sau dreptunghiuri.

În acest articol, vom discuta diferite tipuri de prisme și aria suprafeței formulei prismei, cu exemple și probleme practice.

Cuprins

• Care este suprafața prismei?
• Diferite tipuri de prisme
• Prisma triunghiulara
• Prismă dreptunghiulară
• Prismă pătrată
• Prismă pentagonală
• Prismă hexagonală
• Formula suprafeței prismei
• Aria suprafeței unei prisme Exemple rezolvate
• Practicați probleme pe suprafața unei prisme

Care este suprafața prismei?

Aria suprafeței unei prisme este denumită suprafața totală închisă de toate fețele sale. Pentru a determina suprafața unei prisme, trebuie să calculăm ariile fiecăreia dintre fețele sale și apoi să adăugăm zonele rezultate. O prismă are două tipuri de suprafețe, și anume suprafața laterală și suprafața totală. Zona ocupată de fețele unei prisme, excluzând cele două fețe paralele (bazele unei prisme), este denumită suprafața sa laterală.

Aria suprafeței laterale a unei prisme = [Perimetrul bazei × înălțime] unități pătrate

Acum, aria suprafeței totale a unei prisme este suma ariilor celor două baze ale sale și a suprafeței sale laterale.

Formula generală pentru calcularea suprafeței totale a oricărui tip de prismă dreaptă este:

Suprafața totală a unei prisme = [2 (Aria de bază) + (Perimetrul de bază × înălțime)] unități pătrate

Diferite tipuri de prisme

Există diferite tipuri de prisme în funcție de forma bazei unei prisme, cum ar fi

• prisme triunghiulare,
• prisme pătrate,
• prisme dreptunghiulare,
• prisme pentagonale,
• prisme hexagonale,
• Prisme octogonale.

Prisma triunghiulara

O prismă cu bază triunghiulară este denumită prismă triunghiulară. O prismă triunghiulară este formată din trei suprafețe dreptunghiulare înclinate și două baze triunghiulare paralele. Fie H înălțimea prismei triunghiulare; a, b și c sunt lungimile laturilor, iar h este înălțimea bazelor triunghiulare.

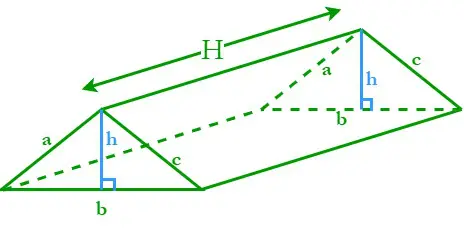
Perimetrul unei baze triunghiulare (P) = Suma celor trei laturi ale sale = a + b + c

Aria unei baze triunghiulare (A) = ½ × bază × înălțime = ½ bh

Știm că formula generală pentru aria suprafeței laterale a unei prisme drepte este L. S. A. = PH, unde P este perimetrul bazei și A este aria bazei.

Prin înlocuirea tuturor valorilor din formula generală obținem ,

Aria suprafeței laterale a unei prisme triunghiulare = (a + b +c)H unități pătrate

Unde,

a, b, c sunt laturile bazei triunghiulare

H este înălțimea prismei triunghiulare

Știm că formula generală pentru suprafața totală a unei prisme drepte este T. S. A. = PH+2A, unde P este perimetrul bazei, A este aria bazei și H este înălțimea prismei.

Prin înlocuirea tuturor valorilor din formula generală obținem

Suprafața totală a prismei triunghiulare = (a + b + c)H + 2 × (½ bh)

Suprafața totală a prismei triunghiulare = (a + b + c)H + bh unități pătrate

Unde,

a, b, c sunt laturile bazei triunghiulare

H este înălțimea prismei triunghiulare

h este înălțimea triunghiului

Prismă dreptunghiulară

O prismă cu bază dreptunghiulară este denumită prismă dreptunghiulară. O prismă dreptunghiulară este formată din patru suprafețe dreptunghiulare și două baze dreptunghiulare paralele. Fie înălțimea prismei h, iar lungimea și lățimea bazelor dreptunghiulare fie l și, respectiv, w .

Perimetrul unei baze dreptunghiulare (P) = Suma celor patru laturi ale sale = 2 (l + w)

Aria unei baze dreptunghiulare (A) = lungime × lățime = l × l

Știm că formula generală pentru suprafața laterală a unei prisme drepte este L. S. A. = PH, unde P este perimetrul bazei și A este aria bazei.

Prin înlocuirea tuturor valorilor din formula generală obținem ,

Aria suprafeței laterale a unei prisme dreptunghiulare = 2h(l + w) unități pătrate

Unde,

l este lungimea

w este lățimea

if else if else if java

h este înălțimea

Știm că formula generală pentru suprafața totală a unei prisme drepte este T. S. A. = PH+2A, unde P este perimetrul bazei, A este aria bazei și H este înălțimea prismei.

Prin înlocuirea tuturor valorilor din formula generală obținem

Suprafața totală a prismei dreptunghiulare = 2h(l + w) + 2(l × w)

= 2 lh + 2 wh + 2 lw

Suprafața totală a prismei dreptunghiulare = 2 (lh + wh + lw) unități pătrate

Unde,

l este lungimea

w este lățimea

h este înălțimea

Prismă pătrată

O prismă cu bază pătrată este denumită prismă pătrată. O prismă pătrată este formată din patru suprafețe dreptunghiulare și două baze pătrate paralele. Fie înălțimea prismei h și lungimile bazelor pătrate s.

Perimetrul unei baze pătrate (P) = Suma celor patru laturi ale sale = s + s + s + s = 4s

Aria unei baze pătrate (A) = (lungimea laturii)²= s²

Știm că formula generală pentru suprafața laterală a unei prisme drepte este L. S. A. = PH, unde P este perimetrul bazei și A este aria bazei.

Prin înlocuirea tuturor valorilor din formula generală obținem,

Aria suprafeței laterale a unei prisme pătrate = 4sh unități pătrate

Unde,

s este latura bazei pătrate

h este înălțimea prismei pătrate

Știm că formula generală pentru suprafața totală a unei prisme drepte este T. S. A. = PH+2A, Unde P este perimetrul bazei, A este aria bazei și H este înălțimea prismei.

Prin înlocuirea tuturor valorilor din formula generală, obținem

Suprafața totală a prismei pătrate = [4sh + 2s ² ] unități pătrate

Unde,

s este latura bazei pătrate

h este înălțimea prismei pătrate

Prismă pentagonală

O prismă cu o bază pentagonală este denumită prismă pentagonală. O prismă pentagonală este formată din cinci suprafețe dreptunghiulare înclinate și două baze pentagonale paralele. Fie h înălțimea prismei pentagonale; a și b să fie lungimea apotemului și lungimile laterale ale bazelor pentagonale.

Perimetrul bazei pentagonului (P) = Suma celor cinci laturi ale sale = 5b

Aria bazei pentagonului (A) = 5/2 x (lungimea apotemului) x (lungimea laturii) = 5ab

Știm că formula generală pentru suprafața laterală a unei prisme drepte este L. S. A. = PH, unde P este perimetrul bazei și A este aria bazei.

Prin înlocuirea tuturor valorilor din formula generală obținem,

Aria suprafeței laterale a unei prisme pentagonale = 5bh unități pătrate

Unde,

b este latura bazei pentagonale

h este înălțimea prismei pentagonale

Știm că formula generală pentru suprafața totală a unei prisme drepte este T. S. A. = PH+2A, unde P este perimetrul bazei, A este aria bazei și H este înălțimea prismei.

Prin înlocuirea tuturor valorilor din formula generală obținem,

Suprafața totală a prismei pentagonale = [5bh + 5ab] unități pătrate

Unde,

b este latura bazei pentagonale

a este lungimea apotema.

h este înălțimea prismei pentagonale

Prismă hexagonală

O prismă cu bază hexagonală este denumită prismă hexagonală. O prismă hexagonală este formată din șase suprafețe dreptunghiulare înclinate și două baze hexagonale paralele. Fie h înălțimea prismei hexagonale; a fie lungimile laterale ale bazelor hexagonale.

Perimetrul unei baze de hexagon (P) = Suma celor șase laturi ale sale = 6a

Aria bazei hexagonale (A) = 6 x (Aria unui triunghi echilateral)

A = 6 x (√3a²/4) ⇒ A = 3√3a²/2

Știm că formula generală pentru suprafața laterală a unei prisme drepte este L. S. A. = PH, unde P este perimetrul bazei și A este aria bazei.

Prin înlocuirea tuturor valorilor din formula generală obținem,

Suprafața laterală a unei prisme hexagonale = 6ah unități pătrate

Unde,

a este latura bazei hexagonale

h este înălțimea bazei hexagonale

Știm că formula generală pentru suprafața totală a unei prisme drepte este T. S. A. = PH+2A, unde P este perimetrul bazei, A este aria bazei și H este înălțimea prismei.

Prin înlocuirea tuturor valorilor din formula generală obținem

Suprafața totală a prismei hexagonale = [6ah +3√3a²] unități pătrate

Unde,

a este latura bazei hexagonale

h este înălțimea bazei hexagonale:

Formula suprafeței prismei

Tabelul de mai jos oferă formula pentru diferite tipuri de prisme:

Aria suprafeței unei prisme Exemple rezolvate

Problema 1: Care este înălțimea unei prisme a cărei suprafață de bază este de 36 de unități pătrate, perimetrul de bază este de 24 de unități și aria sa totală a suprafeței este de 320 de unități pătrate?

Soluţie:

Date date,

Suprafața de bază = 36 de unități pătrate

Perimetrul de bază = 24 de unități

Suprafața totală a prismei = 320 unități pătrate

Avem,

Suprafața totală a prismei = (2 × Suprafața bazei) + (Perimetrul bazei × înălțimea)

⇒ 320 = (2 × 36)+ (24 × h)

⇒ 24h = 248 ⇒ h = 10,34 unități

Prin urmare, înălțimea prismei date este de 10,34 unități.

Problema 2: Aflați aria suprafeței totale a unei prisme pătrate dacă înălțimea prismei și lungimea laturii bazei pătrate sunt de 13 cm, respectiv 4 cm.

Soluţie:

Date date,

Înălțimea prismei pătrate (h) = 13 cm

Lungimea laturii bazei pătrate (a) = 4 cm

Noi stim aia,

np zerouri

Suprafața totală a unei prisme pătrate = 2a²+ 4 ah

= 2 × (4)²+ 4 × 4 × 13

= 32 + 208 = 240 cm²

Prin urmare, suprafața totală a prismei date este de 240 cm².

Problema 3: Determinați lungimea bazei unei prisme pentagonale dacă aria sa totală este de 100 de unități pătrate, iar înălțimea și lungimea apotemelor sunt de 8 unități, respectiv 5 unități.

Soluţie:

Date date,

Suprafața totală a prismei pentagonale = 100 de unități pătrate

Înălțimea prismei (h) = 8 unități

Lungimea apotema (a) = 5 unități

Noi stim aia,

Suprafața totală a prismei pentagonale = 5ab + 5bh

⇒ 100 = 5b (a+ h)

⇒ 100/5 = b (5 + 8)

⇒ 20 = b × (13) ⇒ b = 25/16 = 1,54 unități

Prin urmare, lungimea bazei este de 1,54 unități

Problema 4: Determinați înălțimea prismei dreptunghiulare și aria totală a unei prisme dreptunghiulare dacă suprafața ei laterală este de 540 cm pătrați și lungimea și lățimea bazei sunt de 13 cm, respectiv 7 cm.

Soluţie:

Date date,

Lungimea bazei dreptunghiulare (l) = 13 cm

Lățimea bazei dreptunghiulare (w) = 7 cm

Suprafața laterală a prismei = 540 cm2

Avem,

Suprafața laterală a prismei = perimetrul bazei × înălțime

⇒ 540 = 2 (l + l) h

⇒ 2 (13 + 7) h = 540

⇒ 2 (20) h = 540 ⇒ h = 13,5 cm

Noi stim aia,

Suprafața totală a prismei dreptunghiulare = 2 (lw + wh + lh)

= 2 × (13 × 7 + 7 × (13,5) + 13 × (13,5))

= 2 × (91 + 94,5 + 175,5) = 722 cm²

Prin urmare, înălțimea și suprafața totală a prismei dreptunghiulare date sunt de 13,5 cm și, respectiv, 722 cm pătrați.

Problema 5: Determinați aria suprafeței prismei hexagonale regulate dacă înălțimea prismei este de 12 inchi și lungimea laturii bazei este de 5 inchi.

Soluţie:

Date date,

Înălțimea prismei (h) = 12 in

Lungimea laturii bazei (a) = 6 in

Aria suprafeței unei prisme hexagonale regulate = 6ah + 3√3a²

= 6 × 5 × 12 + 3√3(5)²

= 360 + 75√3

= 360 + 75 × (1,732) = 489,9 inchi pătrați

Prin urmare, aria suprafeței prismei date este de 489,9 sq. in.

Problema 6: Calculați suprafețele laterale și totale ale unei prisme triunghiulare al cărei perimetru de bază este de 25 inci, lungimea și înălțimea bazei triunghiului sunt de 9 inci și 10 inci, iar înălțimea prismei este de 14 inci.

Soluţie:

Date date,

Înălțimea prismei (H) = 14 inci

Perimetrul de bază al prismei (P) = 25 inci

Lungimea bazei triunghiului = 9 inci

Înălțimea triunghiului = 10 inci

Noi stim aia,

Suprafața laterală a prismei = perimetrul bazei × înălțime

= 25 × 14= 350 sq. in

Aria bazei triunghiulare (A) = ½ × bază × înălțime = 1/2 × 9 × 10 = 45 sq. in

Suprafața totală a prismei triunghiulare = 2A + PH

= 2 × 45 + 25 × 14 = 90 + 350 = 440 sq. in

Prin urmare, suprafețele laterale și totale ale prismei sunt de 350 sq. in și, respectiv, 440 sq. in.

Practicați probleme pe suprafața unei prisme

1. Având în vedere o prismă dreptunghiulară cu dimensiuni:

• Lungime = 6 cm
• Latime = 4 cm
• Inaltime = 5 cm

Calculați suprafața totală.

2. Luați în considerare o prismă triunghiulară cu dimensiuni:

• Baza triunghiului = 8 cm
• Înălțimea triunghiului = 6 cm
• Lungimea prismei = 10 cm

Aflați suprafața totală.

3. Determinați aria suprafeței unei prisme pentagonale regulate cu:

• Lungimea laterală a bazei = 7 cm
• Înălțimea prismei = 9 cm.

4. Calculați aria suprafeței unei prisme hexagonale cu:

• Lungimea laturii bazei hexagonale regulate = 10 cm
• Înălțimea prismei = 12 cm.

Suprafața unei prisme – Întrebări frecvente

Ce este o prismă în geometrie?

O prismă este o formă tridimensională cu două baze paralele congruente și fețe laterale dreptunghiulare sau paralelograme care le unesc. Prismele vin sub diferite forme, cum ar fi prisme dreptunghiulare, prisme triunghiulare și prisme pentagonale, fiecare având caracteristici unice.

Cum găsiți suprafața unei prisme?

Pentru a găsi aria suprafeței unei prisme, calculați ariile tuturor fețelor sale și apoi însumați-le. Pentru o prismă dreptunghiulară, formula suprafeței este 2lw + 2lh + 2wh, unde l este lungimea, w este lățimea și h este înălțimea. Pentru alte tipuri de prisme, cum ar fi prismele triunghiulare sau pentagonale, pot fi necesare formule suplimentare pentru aria de bază și aria laterală.

Care sunt proprietățile unei prisme?

Prismele au mai multe proprietăți cheie:

• Au două baze paralele congruente.
• Fețele laterale sunt toate paralelograme.
• Altitudinea (înălțimea) este distanța perpendiculară dintre cele două baze.
• Bazele sunt identice ca formă și dimensiune.
• Secțiunea transversală paralelă cu bazele are întotdeauna aceeași formă și dimensiune ca bazele.

Care sunt câteva exemple din viața reală de prisme?

Prismele pot fi găsite în diferite obiecte și structuri de zi cu zi. Exemplele includ:

• Prisme dreptunghiulare: Clădiri, cutii de cereale, cărți.
• Prisme triunghiulare: Acoperișuri de case, obiecte în formă de pană.
• Prisme pentagonale: Unele tipuri de coloane, anumite structuri arhitecturale.
• Prisme hexagonale: Anumite tipuri de cristale, unele recipiente de ambalare.

De ce este importantă suprafața în prisme?

Suprafața este crucială în prisme, deoarece reprezintă aria totală a tuturor suprafețelor (fețelor) prismei. Înțelegerea suprafeței ajută în diverse aplicații practice, cum ar fi calcularea cantității de material necesară pentru a construi sau acoperi un obiect în formă de prismă, determinarea ratelor de transfer de căldură și optimizarea designului ambalajului.