Forma standard a unei parabole este y = ax2+ bx + c unde a, b și c sunt numere reale și a nu este egal cu zero. O parabolă este definită ca mulțimea tuturor punctelor dintr-un plan care sunt echidistante de o dreaptă fixă și de un punct fix din plan.
În acest articol, vom înțelege ce este o parabolă, ecuația standard a unei parabole, exemple înrudite și altele în detaliu.
Cuprins
- Ce este o parabolă?
- Ecuația unei parabole
- Părți ale unei parabole
- Exemple despre ecuația unei parabole
Ce este o parabolă?
O parabolă este o secțiune conică definită ca mulțime de puncte echidistante de un punct numit focar și de o linie numită directrice. Ecuațiile standard pentru o parabolă depind de orientarea (direcția de deschidere) și de poziție.
Ecuația unei parabole
Ecuația parabolei poate fi scrisă în formă standard sau în formă generală și ambele sunt adăugate mai jos:
Ecuații generale ale unei parabole
Ecuația generală a unei parabole este:
y = 4a(x – h) 2 + k
(sau)
x = 4a(y – k) 2 + h
Unde (h, k) este vârful unei parabole.
Ecuații standard ale unei parabole
Ecuația standard a unei parabole este:
y = ax 2 + bx + c
(sau)
x = este 2 + prin + c
unde, a nu poate fi niciodată zero.
Părți ale unei parabole
Câțiva termeni și părți importante ale unei parabole sunt:
- Focus: Focalizarea este punctul fix al unei parabole.
- Directrix: Directoarea unei parabole este linia perpendiculară pe axa unei parabole.
- Coarda focală: Coarda care trece prin focarul unei parabole, tăind parabola în două puncte distincte, se numește coardă focală.
- Distanța focală: Distanța focală este distanța unui punct (x1, și1) pe parabola din focar.
- Partea dreapta: Un latus rectum este o coardă focală care trece prin focarul unei parabole și este perpendiculară pe axa parabolei. Lungimea latus rectum este LL’ = 4a.
- Excentricitate: Raportul dintre distanța unui punct de la focar și distanța acestuia de la directrixă se numește excentricitate (e). Pentru o parabolă, excentricitatea este egală cu 1, adică e = 1.
O parabolă are patru ecuații standard bazate pe orientarea parabolei și a axei acesteia. Fiecare parabolă are o axă transversală și o axă conjugată diferită.
| Ecuația parabolei | Parabolă | Formule ale parametrilor unei parabole |
|---|---|---|
| și 2 = 4ax | 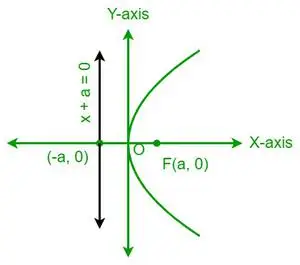 Parabola orizontală |
|
| și 2 = -4ax |  Parabola orizontală |
|
| X 2 = 4 zile |  Parabola verticală |
|
| X 2 = -4 zile |  Parabola verticală |
|
Următoarele sunt observațiile făcute din forma standard a ecuațiilor unei parabole:
- O parabolă este simetrică față de axa ei. De exemplu, y2= 4ax este simetric față de axa x, în timp ce x2= 4ay este simetrică față de axa y.
- Dacă o parabolă este simetrică față de axa x, atunci parabola se deschide spre dreapta dacă coeficientul x este pozitiv și spre stânga dacă coeficientul x este negativ.
- Dacă o parabolă este simetrică față de axa y, atunci parabola se deschide în sus dacă coeficientul y este pozitiv și în jos dacă coeficientul y este negativ.
Următoarele sunt ecuațiile standard ale unei parabole atunci când axa de simetrie este fie paralelă cu axa x, fie cu axa y și vârful nu este la origine.
| Ecuația parabolei | Parabolă | Formule ale parametrilor unei parabole |
|---|---|---|
| (și – k)2= 4a(x – h) |  Parabola orizontală |
|
| (și – k)2= -4a(x – h) |  Parabola orizontală |
|
| (x – h)2= 4a(y – k) |  Parabola verticală |
|
| (x – h)2= -4a(y – k) |  Parabola verticală |
|
Ecuația derivării parabolei
Fie P un punct pe parabolă ale cărui coordonate sunt (x, y). Din definiția unei parabole, distanța punctului P la focar (F) este egală cu distanța aceluiași punct P la directriza unei parabole. Acum, să considerăm un punct X de pe directrice, ale cărui coordonate sunt (-a, y).
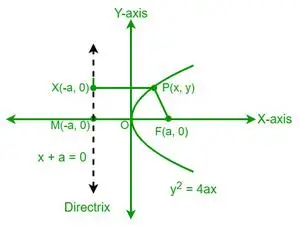
Din definiția excentricității unei parabole, avem
e = PF/PX = 1
⇒ PF = PX
Coordonatele focarului sunt (a, 0). Acum, folosind formula distanței de coordonate, putem găsi distanța punctului P (x, y) la focarul F (a, 0).
PF = √[(x – a)2+ (și – 0)2]
⇒ PF = √[(x – a)2+ și2] ------ (1)
Ecuația directricei este x + a = 0. Pentru a afla distanța lui PX, folosim formula distanței perpendiculare.
PX = (x + a)/√[12+02]
⇒ PX = x +a —————— (2)
Știm deja că PF = PX. Deci, egalați ecuațiile (1) și (2).
√[(x – a)2+ și2] = (x + a)
Prin pătrat pe ambele părți, obținem,
⇒ [(x – a)2+ și2] = (x + a)2
⇒ x2+ a2– 2ax + y2= x2+ a2+ 2x
⇒ și2– 2ax = 2ax
⇒ și2= 2ax + 2ax ⇒ și 2 = 4ax
Astfel, am derivat ecuația unei parabole. În mod similar, putem deriva ecuațiile standard ale celorlalte trei parabole.
- și2= -4ax
- X2= 4 zile
- X2= -4 zile
și 2 = 4ax și 2 = -4ax, x 2 = 4ay și x 2 = -4 zile sunt ecuațiile standard ale unei parabole.
Articole legate de Parabola:
- Ecuația cercului
- Ecuația elipsei
- Ecuația hiperbolei
- Aplicații ale parabolei în viața reală
Exemple despre ecuația unei parabole
Exemplul 1: Aflați lungimea latus rectum, focar și vârf, dacă ecuația parabolei este y 2 = 12x.
Soluţie:
Dat,
Ecuația parabolei este y2= 12x
Comparând ecuația dată cu forma standard y2= 4ax
4a = 12
⇒ a = 12/4 = 3
Noi stim aia,
Partea dreaptă a unei parabole = 4a = 4 (3) = 12
Acum, focalizarea parabolei = (a, 0) = (3, 0)
Vârful parabolei date = (0, 0)
Exemplul 2: Găsiți ecuația parabolei care este simetrică față de axa X și trece prin punctul (-4, 5).
Soluţie:
Dat,
Parabola este simetrică față de axa X și își are vârful la origine.
Astfel, ecuația poate fi de forma y2= 4ax sau y2= -4ax, unde semnul depinde dacă parabola se deschide spre partea stângă sau spre dreapta.
Parabola trebuie să se deschidă la stânga deoarece trece prin (-4, 5) care se află în al doilea cadran.
Deci, ecuația va fi: y2= -4ax
Înlocuind (-4, 5) în ecuația de mai sus,
⇒ (5)2= -4a(-4)
⇒ 25 = 16a
⇒ a = 25/16
Prin urmare, ecuația parabolei este: y2= -4(25/16)x (sau) 4y2= -25x.
Exemplul 3: Găsiți coordonatele focarului, axei, ecuația directricei și latus rectum al parabolei x 2 = 16 ani.
Soluţie:
Dat,
Ecuația parabolei este: x2= 16 ani
Comparând ecuația dată cu forma standard x2= 4 zile,
4a = 16 ⇒ a = 4
Coeficientul lui y este pozitiv, astfel încât parabola se deschide în sus.
De asemenea, axa de simetrie este de-a lungul axei Y pozitive.
Prin urmare,
Focalizarea parabolei este (a, 0) = (4, 0).
Ecuația directricei este y = -a, adică y = -4 sau y + 4 = 0.
Lungimea latus rectum = 4a = 4(4) = 16.
Exemplul 4: Aflați lungimea latus rectum, focar și vârf dacă ecuația unei parabole este 2(x-2) 2 + 16 = y.
Soluţie:
Dat,
Ecuația unei parabole este 2(x-2)2+ 16 = și
Prin compararea ecuației date cu ecuația generală a unei parabole y = a(x – h)2+ k, obținem
a = 2
(h, k) = (2, 16)
Noi stim aia,
Lungimea latus rectum al unei parabole = 4a
= 4(2) = 8
Acum, focus= (a, 0) = (2, 0)
Acum, vârf = (2, 16)
Exemplul 5: Ecuația unei parabole este x 2 – 12x + 4y – 24 = 0, apoi găsiți vârful, focarul și directricea acestuia.
Soluţie:
Dat,
Ecuația parabolei este x2– 12x + 4y – 24 = 0
⇒ x2– 12x + 36 – 36 + 4y – 24 = 0
⇒ (x – 6)2+ 4y – 60 = 0
⇒ (x – 6)2= -4(y + 15)
Ecuația obținută este sub forma (x – h)2= -4a(y – k)
-4a = -4 ⇒ a = 1
Deci, vârful = (h, k) = (6, – 15)
Focalizare = (h, k – a) = (6, -15-1) = (6, -16)
Ecuația directricei este y = k + a
⇒ y = -15 + 1 ⇒ y = -14
⇒ y + 14 = 0
Întrebări frecvente despre ecuația parabolei
Cum găsiți ecuația standard a unei parabole?
Forma standard de parabolă este y2= 4ax sau x2= 4 zile.
Care este ecuația normală a parabolei?
Ecuația normalei la parabola y2= 4ax cu panta m este dat ca: y = mx – 2am – am 3
Cum găsești vârful unei parabole?
Pentru parabola dată: y = ax2+ bx + c vârful său poate fi găsit folosind formula x = − b/2a. Conectați această valoare x înapoi în ecuație pentru a găsi coordonatele y corespunzătoare.
aplicații ascunse
