Sortare rapida este un algoritm intern care se bazează pe strategia de împărțire și cucerire. In acest:
diferența dintre un gigaoctet și un megaoctet
- Matricea de elemente este împărțită în părți în mod repetat, până când nu este posibil să o împarți în continuare.
- Este cunoscut și ca sortarea schimbului de partiții .
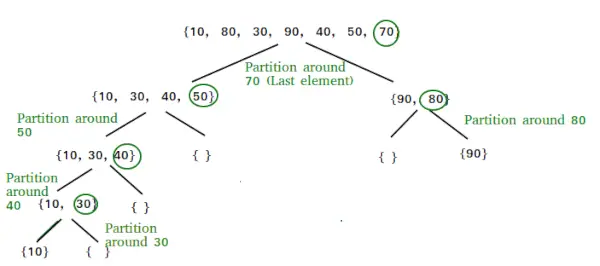
- Utilizează un element cheie (pivot) pentru partiţionarea elementelor.
- O partiție din stânga conține toate acele elemente care sunt mai mici decât pivotul și o partiție din dreapta conține toate acele elemente care sunt mai mari decât elementul cheie.
 Sortare îmbinare este un algoritm extern și se bazează pe strategia de împărțire și cuceri. In acest:
Sortare îmbinare este un algoritm extern și se bazează pe strategia de împărțire și cuceri. In acest:
- Elementele sunt împărțite în două sub-matrice (n/2) din nou și din nou până când rămâne un singur element.
- Merge sort folosește spațiu de stocare suplimentar pentru sortarea matricei auxiliare.
- Merge sort utilizează trei matrice, unde două sunt folosite pentru stocarea fiecărei jumătăți, iar cea de-a treia externă este folosită pentru a stoca lista finală sortată prin îmbinarea altor două și fiecare matrice este apoi sortată recursiv.
- În cele din urmă, toate sub-matricele sunt îmbinate pentru a face dimensiunea „n” elementului matricei.

Sortare rapidă vs Sortare prin îmbinare
- Partiția elementelor din matrice: în sortarea de îmbinare, matricea este împărțită în doar 2 jumătăți (adică n/2). în timp ce în cazul sortării rapide, matricea este împărțită în orice raport. Nu există nicio obligație de a împărți șirul de elemente în părți egale într-o sortare rapidă. Complexitatea celui mai rău caz: complexitatea celui mai rău caz de sortare rapidă este O(n^2), deoarece este nevoie de o mulțime de comparații în cea mai proastă stare. în timp ce în sortarea de îmbinare, cel mai rău caz și cazul mediu au aceleași complexități O(n log n). Utilizare cu seturi de date: sortarea prin îmbinare poate funcționa bine pe orice tip de seturi de date, indiferent de dimensiunea acestuia (fie mare sau mică). întrucât Sortarea rapidă nu poate funcționa bine cu seturi de date mari. Cerință suplimentară de spațiu de stocare: Sortarea prin îmbinare nu este în vigoare deoarece necesită spațiu de memorie suplimentar pentru a stoca matricele auxiliare. în timp ce sortarea rapidă este în vigoare, deoarece nu necesită depozitare suplimentară. Eficiență: sortarea prin îmbinare este mai eficientă și funcționează mai rapid decât sortarea rapidă în cazul unei matrice sau seturi de date mai mari. în timp ce sortarea rapidă este mai eficientă și funcționează mai rapid decât sortarea prin îmbinare în cazul unei matrice mai mici sau seturi de date. Metoda de sortare: Sortarea rapidă este o metodă de sortare internă în care datele sunt sortate în memoria principală. în timp ce sortarea de îmbinare este o metodă de sortare externă în care datele care urmează să fie sortate nu pot fi stocate în memorie și au nevoie de memorie auxiliară pentru sortare. Stabilitate: Sortarea prin îmbinare este stabilă, deoarece două elemente cu valoare egală apar în aceeași ordine în ieșirea sortată ca și în matricea nesortată de intrare. în timp ce Sortarea rapidă este instabilă în acest scenariu. Dar poate fi stabilizat folosind unele modificări ale codului. De preferat pentru : Sortarea rapidă este preferată pentru matrice. în timp ce sortarea Merge este preferată pentru listele legate. Localitate de referință: Quicksort prezintă o localitate bună în cache și acest lucru face sortarea rapidă mai rapidă decât sortarea prin îmbinare (în multe cazuri, cum ar fi mediul de memorie virtuală).
| Baza pentru comparație | Sortare rapida | Merge Sort |
|---|---|---|
| Partiția elementelor din matrice | Împărțirea unei matrice de elemente este în orice raport, nu neapărat împărțită în jumătate. | În sortarea de îmbinare, matricea este împărțită în doar 2 jumătăți (adică n/2). |
| Complexitatea în cel mai rău caz | O(n^2) | O(nlogn) |
| Funcționează bine pe | Funcționează bine pe o matrice mai mică | Funcționează bine pe orice dimensiune de matrice |
| Viteza de executie | Funcționează mai rapid decât alți algoritmi de sortare pentru seturi mici de date, cum ar fi Selection sort etc | Are o viteză constantă pe orice dimensiune de date |
| Cerință suplimentară de spațiu de depozitare | Mai puțin (la loc) | Mai multe (nu pe loc) |
| Eficienţă | Ineficient pentru matrice mai mari | Mai eficient |
| Metoda de sortare | Intern | Extern |
| Stabilitate | Instabil | Grajd |
| De preferat pentru | pentru Arrays | pentru listele conectate |
| Localitatea de referință | bun | sărac |
| Lucrare majora | Lucrarea majoră este să partiționați matricea în două sub-matrice înainte de a le sorta recursiv. | Lucrul major este de a combina cele două sub-matrice după sortarea lor recursiv. |
| Diviziunea matricei | Împărțirea unei matrice în sub-matrice poate fi sau nu echilibrată, deoarece matricea este partiționată în jurul pivotului. | Împărțirea unei matrice în submatrice este întotdeauna echilibrată, deoarece împarte matricea exact la mijloc. |
| Metodă | Sortarea rapidă este o metodă de sortare în loc. | Sortarea prin îmbinare nu este o metodă de sortare în loc. |
| Fuzionarea | Quicksort nu necesită îmbinarea explicită a sub-matricelor sortate; mai degrabă sub-matricele rearanjate corespunzător în timpul partiționării. | Merge sort realizează îmbinarea explicită a sub-matricelor sortate. |
| Spaţiu | Quicksort nu necesită spațiu suplimentar pentru matrice. | Pentru îmbinarea sub-matricelor sortate, are nevoie de o matrice temporară cu dimensiunea egală cu numărul de elemente de intrare. |
