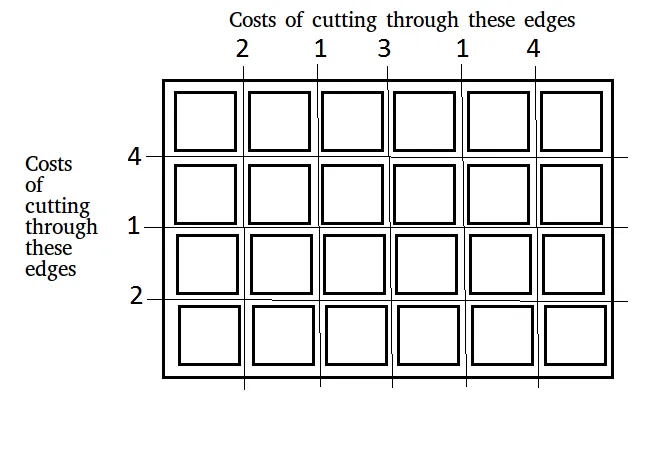
Dată o tablă de dimensiuni n × m care trebuie tăiat în n × m pătrate. Costul efectuării unei tăieturi de-a lungul unei margini orizontale sau verticale este furnizat în două matrice:

• x[] : Reducerea costurilor de-a lungul marginilor verticale (din punct de vedere al lungimii).
• şi[] : Reducerea costurilor de-a lungul marginilor orizontale (din lățime).

Găsiți costul total minim necesar pentru a tăia tabla în pătrate în mod optim.

Exemple: 

Intrare: x[] = [2 1 3 1 4] y[] = [4 1 2] n = 4 m = 6
Ieșire: 42
Explicaţie:

Initial nu. de segmente orizontale = 1 & nr. de segmente verticale = 1.
Modul optim de a tăia în pătrat este:
Alegeți 4 (din x) -> tăiere verticală Cost = 4 × segmente orizontale = 4
 Acum segmente orizontale = 1 segmente verticale = 2.
Alegeți 4 (din y) -> tăiere orizontală Cost = 4 × segmente verticale = 8
 Acum segmente orizontale = 2 segmente verticale = 2.
Alegeți 3 (din x) -> tăiere verticală Cost = 3 × segmente orizontale = 6
 Acum segmente orizontale = 2 segmente verticale = 3.
Alegeți 2 (din x) -> tăiere verticală Cost = 2 × segmente orizontale = 4
 Acum segmente orizontale = 2 segmente verticale = 4.
Alegeți 2 (din y) -> tăiere orizontală Cost = 2 × segmente verticale = 8
 Acum segmente orizontale = 3 segmente verticale = 4.
Alegeți 1 (din x) -> tăiere verticală Cost = 1 × segmente orizontale = 3
Acum segmente orizontale = 3 segmente verticale = 5.
Alegeți 1 (din x) -> tăiere verticală Cost = 1 × segmente orizontale = 3
Acum segmente orizontale = 3 segmente verticale = 6.
Alegeți 1 (din y) -> tăiere orizontală Cost = 1 × segmente verticale = 6
Acum segmente orizontale = 4 segmente verticale = 6.
Deci costul total = 4 + 8 + 6 + 4 + 8 + 3 + 3 + 6 = 42.

Intrare: x[] = [1 1 1] y[] = [1 1 1] n = 4 m = 4
Ieșire: 15
Explicaţie:
Initial nu. de segmente orizontale = 1 & nr. de segmente verticale = 1.
Modul optim de a tăia în pătrat este:
Alegeți 1 (din y) -> tăiere orizontală Cost = 1 × segmente verticale = 1
Acum segmente orizontale = 2 segmente verticale = 1.
Alegeți 1 (din y) -> tăiere orizontală Cost = 1 × segmente verticale = 1
Acum segmente orizontale = 3 segmente verticale = 1.
Alegeți 1 (din y) -> tăiere orizontală Cost = 1 × segmente verticale = 1
Acum segmente orizontale = 4 segmente verticale = 1.
Alegeți 1 (din x) -> tăiere verticală Cost = 1 × segmente orizontale = 4
Acum segmente orizontale = 4 segmente verticale = 2.
Alegeți 1 (din x) -> tăiere verticală Cost = 1 × segmente orizontale = 4
Acum segmente orizontale = 4 segmente verticale = 3.
Alegeți 1 (din x) -> tăiere verticală Cost = 1 × segmente orizontale = 4
Acum segmente orizontale = 4 segmente verticale = 4
Deci costul total = 1 + 1 + 1 + 4 + 4 + 4 = 15.

Cuprins

• [Abordare naivă] Încercați toate permutările - O((n+m)!×(n+m)) Timp și O(n+m) Spațiu
• [Abordare așteptată] Folosind Tehnica Greedy - O( n (log n)+m (log m)) Timp și O (1) spațiu

[Abordare naivă] Încercați toate permutările - O((n+m)!×(n+m)) Timp și O(n+m) Spațiu

Ideea este de a genera toate permutările posibile ale tăierilor date și apoi de a calcula costul pentru fiecare permutare. În sfârșit, returnați costul minim printre ele.

Nota: Această abordare nu este fezabilă pentru intrări mai mari, deoarece numărul de permutări crește factorial ca (m+n-2)!.
Pentru fiecare permutare trebuie să calculăm costul în timp O(m+n). Prin urmare, complexitatea generală a timpului devine O((m+n−2)!×(m+n)).

[Abordare așteptată] Folosind Tehnica Greedy - O( n (log n)+m (log m)) Timp și O (1) spațiu

Ideea este să faceți mai întâi cele mai scumpe tăieturi folosind a abordare lacomă . Observația este că alegerea celei mai mari reduceri a costurilor la fiecare pas reduce costurile viitoare prin afectarea mai multor piese simultan. Sortăm costurile verticale (x) și orizontale (y) tăiate în ordine descrescătoare, apoi alegem iterativ pe cea mai mare pentru a maximiza economiile de costuri. Tăieturile rămase sunt procesate separat pentru a se asigura că toate secțiunile sunt împărțite în mod optim.

Ce se întâmplă când facem o tăietură?

• Tăiere orizontală → tăiați pe lățime astfel încât numărul de benzi orizontale crește (hCount++). Dar costul este înmulțit cu vCount (numărul de benzi verticale), deoarece tăietura orizontală trebuie să treacă prin toate segmentele verticale.
• Tăiere verticală → tăiați pe înălțime astfel încât numărul de benzi verticale crește (vCount++). Dar costul este înmulțit cu hCount (numărul de benzi orizontale) deoarece tăietura verticală trebuie să treacă prin toate segmentele orizontale.

Pași pentru a rezolva problema:

• Sortați atât matricele x și y în ordine descrescătoare.
• Folosiți două indicatori unul pentru x și unul pentru y pornind de la cea mai mare valoare și trecând spre valori mai mici.
• Mențineți hCount și vCount pentru a urmări câte segmente afectează fiecare tăietură și actualizați-le în consecință.
• Repetați în timp ce atât x și y au reduceri neprocesate, alegând întotdeauna costul mai mare pentru a minimiza cheltuielile totale.
• Dacă x are tăieturi rămase, procesează-le cu hCount multiplicator; procesați în mod similar tăierile y rămase cu vCount.
• Acumulați costul total la fiecare pas folosind formula: costul redus * numărul de piese afectate asigurând un cost minim.

#include   #include #include   using namespace std; int minCost(int n int m   vector<int>& x vector<int>& y) {    // Sort the cutting costs in ascending order  sort(x.begin() x.end());  sort(y.begin() y.end());   int hCount = 1 vCount = 1;   int i = x.size() - 1 j = y.size() - 1;   int totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;   vCount++;  i--;  }   else {  totalCost += y[j] * vCount;   hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost; } int main() {    int n = 4 m = 6;  vector<int> x = {2 1 3 1 4};  vector<int> y = {4 1 2};  cout << minCost(n m x y) << endl;  return 0; } 

import java.util.Arrays; class GfG {    static int minCost(int n int m   int[] x int[] y) {    // Sort the cutting costs in ascending order  Arrays.sort(x);  Arrays.sort(y);   int hCount = 1 vCount = 1;   int i = x.length - 1 j = y.length - 1;   int totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;   vCount++;  i--;  }   else {  totalCost += y[j] * vCount;   hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost;  }  public static void main(String[] args) {    int n = 4m = 6;  int[] x = {2 1 3 1 4};  int[] y = {4 1 2};  System.out.println(minCost(n m x y));  } } 

def minCost(nm x y): # Sort the cutting costs in ascending order x.sort() y.sort() hCount vCount = 1 1 i j = len(x) - 1 len(y) - 1 totalCost = 0 while i >= 0 and j >= 0: # Choose the larger cost cut to  # minimize future costs if x[i] >= y[j]: totalCost += x[i] * hCount vCount += 1 i -= 1 else: totalCost += y[j] * vCount hCount += 1 j -= 1 # Process remaining vertical cuts while i >= 0: totalCost += x[i] * hCount vCount += 1 i -= 1 # Process remaining horizontal cuts while j >= 0: totalCost += y[j] * vCount hCount += 1 j -= 1 return totalCost if __name__ == '__main__': nm = 4 6 x = [2 1 3 1 4] y = [4 1 2] print(minCost(nmx y)) 

using System; class GfG {  public static int minCost(int n int m   int[] x int[] y) {    // Sort the cutting costs in ascending order  Array.Sort(x);  Array.Sort(y);  int hCount = 1 vCount = 1;  int i = x.Length - 1 j = y.Length - 1;  int totalCost = 0;  // Process the cuts in greedy manner  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  else {  totalCost += y[j] * vCount;  hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost;  }    public static void Main() {    int n=4m=6;  int[] x = {2 1 3 1 4};  int[] y = {4 1 2};  Console.WriteLine(minCost(nm x y));  } } 

function minCost( nm x y) {    // Sort the cutting costs in ascending order  x.sort((a b) => a - b);  y.sort((a b) => a - b);  let hCount = 1 vCount = 1;  let i = x.length - 1 j = y.length - 1;  let totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;  vCount++;  i--;  }   else {  totalCost += y[j] * vCount;  hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost; } // Driver Code let n = 4m = 6; let x = [2 1 3 1 4]; let y = [4 1 2]; console.log(minCost(nm x y)); 

42