Programare liniară este un concept matematic care este folosit pentru a găsi soluția optimă a funcției liniare. Această metodă utilizează ipoteze simple pentru optimizarea funcției date. Programarea liniară are o aplicație uriașă în lumea reală și este folosită pentru a rezolva diferite tipuri de probleme.
Programarea liniară este utilizată în diverse industrii, cum ar fi industriile de transport maritim, industriile de producție, industriile de transport, telecomunicații și altele.
Termenul programare liniară constă din două cuvinte liniar și programare, cuvântul liniar spune relația dintre diferitele tipuri de variabile de gradul unu utilizate într-o problemă și cuvântul programare ne spune procedura pas cu pas pentru a rezolva aceste probleme.
În acest articol, vom afla în detaliu despre programarea liniară, exemplele, formulele și alte concepte.
Cuprins
- Ce este programarea liniară?
- Componentele programării liniare
- Exemple de programare liniară
- Probleme de programare liniară
- Tipuri de probleme de programare liniară
- Formula de programare liniară
- Cum se rezolvă problemele de programare liniară?
- Metode de programare liniară
- Metoda Simplex de programare liniară
- Metoda grafică de programare liniară
- Aplicații de programare liniară
- Importanța programării liniare
- Aplicații actualizate ale programării liniare
- Programarea liniară în cercetarea operațională
- Metoda Simplex
Ce este programarea liniară?
Programare liniară sau Optimizare liniară este o tehnică care ne ajută să găsim soluția optimă pentru o anumită problemă, o soluție optimă este o soluție care este cel mai bun rezultat posibil al unei anumite probleme.
În termeni simpli, este metoda de a afla cum să faci ceva în cel mai bun mod posibil. Cu resurse limitate, trebuie să utilizați în mod optim resursele și să obțineți cel mai bun rezultat posibil într-un anumit obiectiv, cum ar fi cel mai mic cost, cea mai mare marjă sau cel mai mic timp.
Situația care necesită căutarea celor mai bune valori ale variabilelor supuse anumitor constrângeri este cea în care folosim probleme de programare liniară. Aceste situații nu pot fi gestionate de tehnicile uzuale de calcul și numerice.
Definiție programare liniară
Programarea liniară este tehnica utilizată pentru optimizarea unui anumit scenariu. Utilizarea programării liniare ne oferă cel mai bun rezultat posibil într-o situație dată. Utilizează toate resursele disponibile astfel încât să producă rezultatul optim.
Componentele programării liniare
Componentele de bază ale unei probleme de programare liniară (LP) sunt:
- Variabile de decizie: Variabilele pe care doriți să le determinați pentru a obține soluția optimă.
- Funcția obiectivă: M ecuație atematică care reprezintă scopul pe care doriți să-l atingeți
- Constrângeri: Limitări sau restricții pe care trebuie să le respecte variabilele de decizie.
- Restricții de non-negativitate: În unele scenarii din lumea reală, variabilele de decizie nu pot fi negative
Caracteristici suplimentare ale programării liniare
- Finitudine: Numărul de variabile de decizie și constrângeri într-o problemă LP este finit.
- Linearitate: Funcția obiectiv și toate constrângerile trebuie să fie funcții liniare ale variabilelor de decizie . Înseamnă că gradul variabilelor ar trebui să fie unul.
Exemple de programare liniară
Putem înțelege situațiile în care se aplică programarea liniară cu ajutorul exemplului discutat mai jos,
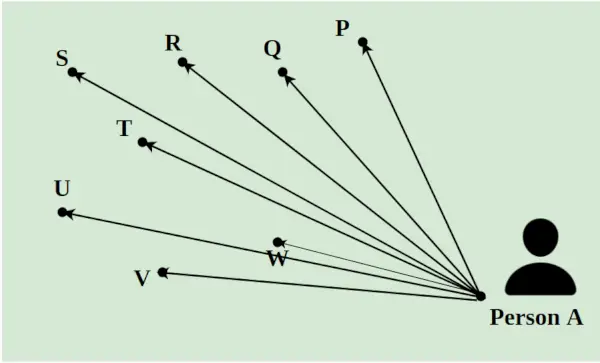
Să presupunem că un livrător trebuie să livreze 8 pachete într-o zi în diferite locații ale unui oraș. El trebuie să aleagă toate pachetele din A și trebuie să le livreze în punctele P, Q, R, S, T, U, V și W. Distanța dintre ele este indicată folosind liniile așa cum se arată în imaginea de mai jos. Cea mai scurtă cale urmată de livrător este calculată folosind conceptul de Programare Liniară.
explicați independența datelor
Probleme de programare liniară
Probleme de programare liniară (LPP) implică optimizarea unei funcții liniare pentru a găsi soluția optimă a valorii pentru funcție. Valoarea optimă poate fi fie valoarea maximă, fie valoarea minimă.
În LPP, funcțiile liniare sunt numite functii obiective. O funcție obiectiv poate avea mai multe variabile, care sunt supuse unor condiții și trebuie să satisfacă constrângeri liniare .
Tipuri de probleme de programare liniară
Există multe probleme diferite de programare liniară (LPP), dar ne vom ocupa de trei probleme majore de programare liniară în acest articol.
Probleme de fabricație
Problemele de fabricație sunt o problemă care tratează numărul de unități care ar trebui produse sau vândute pentru a maximiza profiturile atunci când fiecare produs necesită forță de muncă fixă, ore de mașină și materii prime.
Probleme cu dieta
Este folosit pentru a calcula numărul de diferite tipuri de constituenți care trebuie incluse în dietă pentru a obține costul minim, în funcție de disponibilitatea alimentelor și prețurile acestora.
Probleme de transport
Este folosit pentru a determina programul de transport pentru a găsi cea mai ieftină modalitate de a transporta un produs de la fabrici/fabrici situate în locații diferite către piețe diferite.
Formula de programare liniară
O problemă de programare liniară constă în,
- Variabile de decizie
- Funcție obiectivă
- Constrângeri
- Restricții non-negative
Variabile de decizie sunt variabilele x și y, care decid rezultatul problemei de programare liniară și reprezintă soluția finală.
The funcție obiectivă , reprezentată în general de Z, este funcția liniară care trebuie optimizată în funcție de condiția dată pentru a obține soluția finală.
The restricții impuse variabilelor de decizie care le limitează valorile se numesc constrângeri.
Acum, formula generală a unei probleme de programare liniară este:
Funcție obiectivă : Z = ax + by
Constrângeri: cx + dy ≥ e, px + qy ≤ r
Restricții non-negative: x ≥ 0, y ≥ 0
În condiția de mai sus, x și y sunt variabilele de decizie.
Cum se rezolvă problemele de programare liniară?
Înainte de a rezolva problemele de programare liniară trebuie mai întâi să formulăm problemele conform parametrilor standard. Pașii pentru rezolvarea problemelor de programare liniară sunt:
Pasul 1: Marcați variabilele de decizie din problemă.
Pasul 2: Construiți funcția obiectivă a problemei și verificați dacă funcția trebuie minimizată sau maximizată.
Pasul 3: Notați toate constrângerile problemelor liniare.
Pasul 4: Asigurați restricții nenegative ale variabilelor de decizie.
Pasul 5: Acum rezolvăm problema de programare liniară folosind orice metodă, în general, folosim fie metoda simplex, fie metoda grafică.
Metode de programare liniară
Folosim diverse metode pentru rezolvarea problemelor de programare liniară. Cele mai frecvente două metode utilizate sunt:
- Metoda Simplex
- Metoda grafică
Să învățăm despre aceste două metode în detaliu în acest articol,
Metoda simplex de programare liniară
Una dintre cele mai comune metode de rezolvare a problemei de programare liniară este metoda simplex. În această metodă, repetăm o anumită condiție „n” de mai multe ori până când se obține o soluție optimă.
Pașii necesari pentru rezolvarea problemelor de programare liniară folosind metoda simplex sunt:
Pasul 1: Formulați problemele de programare liniară pe baza constrângerilor date.
Pasul 2: Convertiți toate inegalitățile date în ecuații sau egalități ale problemelor de programare liniară adăugând variabila slack la fiecare inegalitate acolo unde este necesar.
Pasul 3: Construiți tabelul simplex inițial. Reprezentând fiecare ecuație de constrângere într-un rând și scriind funcția obiectiv pe rândul de jos. Tabelul astfel obținut se numește tabel Simplex.
Pasul 4: Identificați cea mai mare intrare negativă în rândul de jos coloana elementului cu cea mai mare intrare negativă se numește coloana pivot
Pasul 5: Împărțiți intrările coloanei din dreapta cu intrările coloanei pivot respective, excluzând intrările din rândul cel mai de jos. Acum rândul care conține cea mai mică intrare se numește rând pivot. Elementul pivot este obținut prin intersecția rândului pivot și coloanei pivot.
Pasul 6: Folosind operația cu matrice și cu ajutorul elementului pivot faceți ca toate intrările din coloana pivot să fie zero.
Pasul 7: Verificați intrările nenegative din rândul de jos dacă nu există intrări negative în rândul de jos, încheiați procesul, altfel începeți procesul din nou de la pasul 4.
Pasul 8: Tabelul simplex final astfel obținut oferă soluția problemei noastre.
Metoda grafică de programare liniară
Metoda grafică este o altă metodă decât metoda Simplex, care este folosită pentru a rezolva probleme de programare liniară. După cum sugerează și numele, această metodă folosește grafice pentru a rezolva problemele de programare liniară date. Aceasta este cea mai bună metodă pentru a rezolva probleme de programare liniară și necesită mai puțin efort decât metoda simplex.
În timp ce folosim această metodă, reprezentăm grafic toate inegalitățile care sunt supuse constrângerilor în problemele de programare liniară date. De îndată ce toate inegalitățile LPP date sunt reprezentate în graficul XY, regiunea comună a tuturor inegalităților oferă soluția optimă. Se calculează toate punctele de colț ale regiunii fezabile și se calculează valoarea funcției obiectiv în toate acele puncte, apoi comparând aceste valori obținem soluția optimă a LPP.
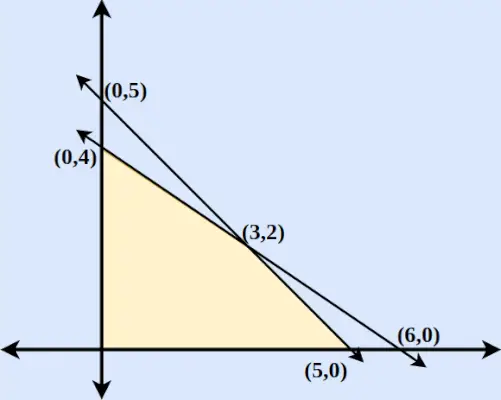
Exemplu: Găsiți valoarea maximă și minimă a lui z = 6x + 9y când condițiile de constrângere sunt:
- 2x + 3y ≤ 12
- x și y ≥ 0
- x + y ≤ 5
Soluţie:
Pasul 1 : Mai întâi convertiți inecuațiile în ecuații normale. Prin urmare, ecuațiile vor fi 2x+3y = 0, x = 0, y = 0 și x + y = 5.
Pasul 2 : Aflați punctele în care 2x + 3y și x + y = 5 taie axa x și axa y. Pentru a găsi punctul de intersecție al axei x puneți y = 0 în ecuația respectivă și găsiți punctul. În mod similar, pentru punctele de intersecție pe axa y puneți x = 0 în ecuația respectivă.
Pasul 3 : Desenați cele două linii tăind axa x și axa y. Constatăm că cele două axe se taie reciproc la (3,2).
Pasul 4 : Pentru x ≥ 0 și y ≥ 0, constatăm că ambele inecuații sunt urmate. Prin urmare, regiunea va include o regiune arie închisă de două axe și ambele linii incluzând originea. Regiunea trasată este prezentată mai jos în figură.
Pasul 5 : Găsiți Z pentru fiecare punct și maxime și minime.
Coordonatele Z = 6x + 9y (0,5) Z = 45 (0,4) Z = 36 (5,0) Z = 30 (6,0) Z = 36 (3,2) Z = 36 Prin urmare, aflăm că Z = 6x + 9y este maxim la (0,5) și minim la (5,0).
Aplicații de programare liniară
Programarea liniară are aplicații în diverse domenii. Este folosit pentru a găsi costul minim al unui proces atunci când sunt date toate constrângerile problemelor. Este folosit pentru a optimiza costul de transport al vehiculului, etc. Diverse aplicații ale programării liniare sunt
Industrii Inginerie
Industriile de inginerie utilizează programarea liniară pentru a rezolva problemele de proiectare și fabricație și pentru a obține rezultatul maxim dintr-o anumită condiție.
Industrii manufacturiere
Industriile de producție folosesc programarea liniară pentru a maximiza profitul companiilor și pentru a reduce costurile de producție.
Industriile Energetice
Companiile energetice folosesc programarea liniară pentru a-și optimiza producția.
Industriile Transporturilor
Programarea liniară este, de asemenea, utilizată în industriile de transport pentru a găsi calea de a minimiza costul de transport.
Importanța programării liniare
Programarea liniară are o importanță uriașă în diverse industrii, maximizează valoarea de ieșire, minimizând în același timp valorile de intrare în funcție de diverse constrângeri.
LP este foarte aplicabil atunci când avem mai multe condiții în timpul rezolvării unei probleme și trebuie să optimizăm rezultatul problemei, adică fie trebuie să găsim valoarea minimă, fie valoarea maximă în funcție de o anumită condiție.
Citeşte mai mult,
- Inegalități liniare
- Soluția algebrică a inegalităților liniare
Probleme de programare liniară
Problema 1: O companie produce și vinde două tipuri de produse, iar costul de producție al fiecărei unități a și b este de 200 și respectiv 150 de rupii, fiecare unitate de produs aduce un profit de 20 de rupii și fiecare unitate de produs b are un profit de 15 rupii la vânzare. . Compania estimează că cererea lunară pentru A și B este la maximum din unitatea recoltată în tot bugetul de producție al lunii este stabilit la 50000 de rupii. Câte unități ar trebui să producă compania pentru a obține profit maxim din vânzările sale lunare dintr-un si b?
Soluţie:
Fie x = numărul de unități de tip A
y = Numărul de unități de tip B
Maximizați Z = 40x + 50y
Sub rezerva constrângerilor
3x + y ≤ 9
x + 2y ≤ 8
și x, y ≥ 0
Luați în considerare ecuația,
3x + y = 9
x = 3
y = 0
și x + 2y = 8
x = 8
y = 0
Acum, putem determina valoarea maximă a lui Z evaluând valoarea lui Z în cele patru puncte (vârfurile) prezentate mai jos
Noduri
Z = 40x + 50y
(0, 0)
string.compare c#Z = 40 × 0 + 50 × 0 = Rs. 0
(3, 0)
Z = 40 × 3 + 50 × 0 = Rs. 120
(0, 4)
Z = 40 × 0 + 50 × 4 = Rs. 200
(23)
Z = 40 × 2 + 50 × 3 = Rs. 230
Profit maxim, Z = Rs. 230
∴ Numărul de unități de tip A este 2 și numărul de unități de tip B este 3.
Problema 2: Maximizați Z = 3x + 4y.
Sub rezerva constrângerilor, x + y ≤ 450, 2x + y ≤ 600 și x, y ≤ 0.
Soluţie:
Avem din dat
Constrângeri (1)
X + Y = 450
Punând x = 0, ⇒ 0 + y = 450 ⇒ y = 450
Punând y = 0, ⇒ x + 0 = 450 ⇒ x = 450
Din, Constrângeri (2)
2x + y = 600
Punând x = 0, ⇒ 0 + y = 600 ⇒ y = 600
Punând y = 0, ⇒ 2x + 0 = 600 ⇒ x = 300
Acum, avem coordonatele punctelor Z = 3x + 4y
| Noduri | Z = 3x + 4y |
|---|---|
| (0, 0) | Z = 3 × 0 + 4 × 0 = 0 |
| (300, 0) | Z = 3 × 300+ 4 × 0 = 900 |
| (150, 300) | Z = 3 × 150 + 4 × 300 = 1650 |
| (0, 450) | Z = 3 × 0 + 4 × 450 = 1800 |
Prin urmare, soluția optimă maximă Z = 1800 la coordonatele x = 0 și y = 450. Graficul este prezentat mai jos.

Aplicații actualizate ale programării liniare
Programarea liniară, o tehnică matematică puternică, este utilizată pentru a rezolva probleme de optimizare în diverse industrii. Iată câteva aplicații moderne:
- Optimizarea lanțului de aprovizionare : Programarea liniară ajută companiile să minimizeze costurile și să maximizeze eficiența în lanțurile lor de aprovizionare. Este folosit pentru a determina cele mai rentabile rute de transport, operațiuni de depozit și strategii de gestionare a stocurilor.
- Managementul energiei : În sectorul energetic, programarea liniară este utilizată pentru a optimiza mixul de metode de producere a energiei. Aceasta include echilibrarea surselor de energie tradiționale cu cele regenerabile pentru a reduce costurile și impactul asupra mediului, în timp ce satisface cererea.
- Proiectarea rețelelor de telecomunicații : Programarea liniară ajută la proiectarea rețelelor de telecomunicații eficiente. Ajută la alocarea lățimii de bandă, la proiectarea structurilor de rețea și la optimizarea fluxului de date pentru a asigura o comunicare de mare viteză la costuri mai mici.
- Planificare financiara : Companiile și analiștii financiari folosesc programarea liniară pentru optimizarea portofoliului, managementul riscului și bugetarea capitalului. Ajută la luarea deciziilor de investiții care maximizează rentabilitatea, reducând în același timp riscul.
- Logistica asistenței medicale : În asistența medicală, programarea liniară este aplicată pentru a optimiza alocarea resurselor, cum ar fi paturile de spital, personalul medical și echipamentele. Este esențial pentru îmbunătățirea îngrijirii pacienților, reducerea timpilor de așteptare și gestionarea eficientă a costurilor.
- Optimizarea procesului de fabricație : Programarea liniară este utilizată pentru a determina nivelurile optime de producție pentru mai multe produse dintr-o unitate de producție, luând în considerare constrângeri precum forța de muncă, materialele și disponibilitatea mașinii.
- Planificarea Agricolă : Fermierii și planificatorii agricoli folosesc programarea liniară pentru a decide cu privire la selecția culturilor, utilizarea terenurilor și alocarea resurselor pentru a maximiza randamentele și profiturile, conservând în același timp resursele.
- Programarea echipajului companiei aeriene : Companiile aeriene folosesc programare liniară pentru a programa eficient echipajele, asigurându-se că zborurile sunt dotate cu personal în conformitate cu reglementările și reducând la minimum costurile operaționale.
Aceste aplicații demonstrează versatilitatea și puterea programării liniare în rezolvarea problemelor complexe de optimizare în diverse sectoare, arătându-și relevanța în lumea actuală bazată pe date.
Programarea liniară în cercetarea operațională
- Instrumentul de bază : Programarea liniară este un instrument de bază în cercetarea operațională pentru optimizarea resurselor.
- Luarea deciziilor : Ajută la luarea celor mai bune decizii privind alocarea resurselor, maximizarea profiturilor sau minimizarea costurilor.
- Aplicații largi : Folosit în diverse domenii, cum ar fi logistică, producție, finanțe și asistență medicală pentru rezolvarea problemelor complexe.
- Modelarea problemelor din lumea reală : Transformă problemele din lumea reală în modele matematice pentru a găsi cele mai eficiente soluții.
Metoda Simplex
- Algoritm de optimizare : Metoda Simplex este un algoritm puternic utilizat în programarea liniară pentru a găsi soluția optimă la inegalitățile liniare.
- Abordare pas cu pas : Se îndreaptă iterativ către cea mai bună soluție navigând pe marginile regiunii fezabile definite de constrângeri.
- Eficienţă : Cunoscut pentru eficiența sa în rezolvarea problemelor de programare liniară la scară largă.
- Versatilitate : Aplicabil în diferite domenii, cum ar fi planificarea dietei, fluxurile de rețea, programarea producției și multe altele, prezentându-și versatilitatea.
Programare liniară – Întrebări frecvente
Ce este programarea liniară?
Programarea liniară este un concept matematic care este utilizat pentru a optimiza o problemă liniară dată care are o varietate de constrângeri. Folosind programarea liniară obținem rezultatul optim al problemei date
Ce sunt problemele de programare liniară?
Problemele de programare liniară (LPP) sunt problemele care oferă soluția optimă condițiilor date.
Ce este formula de programare liniară?
Formulele generale de programare liniară sunt:
- Funcția obiectivă: Z = ax + by
- Constrângeri: px + qy ≤ r, sx + ty ≤ u
- Restricții nenegative: x ≥ 0, y ≥ 0
Care sunt diferitele tipuri de programare liniară?
Diferite tipuri de metode de programare liniară sunt:
- Programare liniară prin metoda simplex
- Programare liniară prin metoda R
- Programare liniară prin metoda grafică
Care sunt cerințele programării liniare?
Diverse cerințe ale problemelor de programare liniară sunt:
- Liniaritate
- Funcție obiectivă
- Constrângeri
- Non-negativitate
Care sunt avantajele programării liniare?
Diverse avantaje ale programării liniare sunt:
- Oferă soluția optimă pentru orice problemă liniară dată.
- Este ușor de utilizat și oferă întotdeauna rezultate consistente
- Ajută la maximizarea profiturilor și la reducerea costurilor de intrare.