Având în vedere rădăcina lui a Arborele de căutare binar și un număr întreg k . Sarcina este de a găsi cel mai mare număr mai puțin decât sau egal la k dacă nu există un astfel de element se imprimă -1.
java convertește caracterul în șir
Exemple:
Intrare:

Ieșire: 21
Explicatie: 19 și 25 sunt două numere cele mai apropiate de 21 și 19 este cel mai mare număr având o valoare mai mică sau egală cu 21.
Intrare: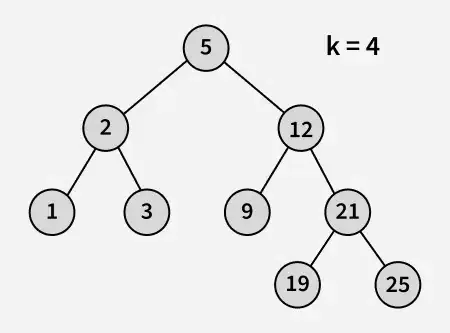
Ieșire: 3
Explicatie: 3 și 5 sunt două numere cele mai apropiate de 4 și 3 este cel mai mare număr având o valoare mai mică sau egală cu 4.
Cuprins
- [Abordare naivă] Utilizarea recursiunii - O(h) Timp și O(h) spațiu
- [Abordare așteptată] Folosind iterația - O(h) Timp și O(1) Spațiu
[Abordare naivă] Utilizarea recursiunii - O(h) Timp și O(h) spațiu
C++Ideea este să începem de la rădăcină și comparați valoarea sa cu k. Dacă valoarea nodului este mai mare decât k, treceți în subarborele din stânga. În caz contrar, găsiți valoarea celui mai mare număr mai mic decât egal cu k în subarborele drept . Dacă subarborele din dreapta returnează -1 (adică nu există o astfel de valoare), atunci returnează valoarea nodului curent. Altfel returnează valoarea returnată de subarborele din dreapta (deoarece va fi mai mare decât valoarea nodului curent, dar mai mică decât egală cu k).
// C++ code to find the largest value // smaller than or equal to k using recursion #include
// Java code to find the largest value // smaller than or equal to k using recursion class Node { int data; Node left right; Node(int val) { data = val; left = null; right = null; } } class GfG { // function to find max value less than k static int findMaxFork(Node root int k) { // Base cases if (root == null) return -1; if (root.data == k) return k; // If root's value is smaller // try in right subtree else if (root.data < k) { int x = findMaxFork(root.right k); if (x == -1) return root.data; else return x; } // If root's data is greater // return value from left subtree. return findMaxFork(root.left k); } public static void main(String[] args) { int k = 24; // creating following BST // // 5 // / // 2 12 // / / // 1 3 9 21 // / // 19 25 Node root = new Node(5); root.left = new Node(2); root.left.left = new Node(1); root.left.right = new Node(3); root.right = new Node(12); root.right.left = new Node(9); root.right.right = new Node(21); root.right.right.left = new Node(19); root.right.right.right = new Node(25); System.out.println(findMaxFork(root k)); } }
# Python code to find the largest value # smaller than or equal to k using recursion class Node: def __init__(self val): self.data = val self.left = None self.right = None # function to find max value less than k def findMaxFork(root k): # Base cases if root is None: return -1 if root.data == k: return k # If root's value is smaller # try in right subtree elif root.data < k: x = findMaxFork(root.right k) if x == -1: return root.data else: return x # If root's data is greater # return value from left subtree. return findMaxFork(root.left k) if __name__ == '__main__': k = 24 # creating following BST # # 5 # / # 2 12 # / / # 1 3 9 21 # / # 19 25 root = Node(5) root.left = Node(2) root.left.left = Node(1) root.left.right = Node(3) root.right = Node(12) root.right.left = Node(9) root.right.right = Node(21) root.right.right.left = Node(19) root.right.right.right = Node(25) print(findMaxFork(root k))
// C# code to find the largest value // smaller than or equal to k using recursion using System; class Node { public int data; public Node left right; public Node(int val) { data = val; left = null; right = null; } } class GfG { // function to find max value less than k static int FindMaxFork(Node root int k) { // Base cases if (root == null) return -1; if (root.data == k) return k; // If root's value is smaller // try in right subtree else if (root.data < k) { int x = FindMaxFork(root.right k); if (x == -1) return root.data; else return x; } // If root's data is greater // return value from left subtree. return FindMaxFork(root.left k); } static void Main() { int k = 24; // creating following BST // // 5 // / // 2 12 // / / // 1 3 9 21 // / // 19 25 Node root = new Node(5); root.left = new Node(2); root.left.left = new Node(1); root.left.right = new Node(3); root.right = new Node(12); root.right.left = new Node(9); root.right.right = new Node(21); root.right.right.left = new Node(19); root.right.right.right = new Node(25); Console.WriteLine(FindMaxFork(root k)); } }
// JavaScript code to find the largest value // smaller than or equal to k using recursion class Node { constructor(val) { this.data = val; this.left = null; this.right = null; } } // function to find max value less than k function findMaxFork(root k) { // Base cases if (root === null) return -1; if (root.data === k) return k; // If root's value is smaller // try in right subtree else if (root.data < k) { let x = findMaxFork(root.right k); if (x === -1) return root.data; else return x; } // If root's data is greater // return value from left subtree. return findMaxFork(root.left k); } let k = 24; // creating following BST // // 5 // / // 2 12 // / / // 1 3 9 21 // / // 19 25 let root = new Node(5); root.left = new Node(2); root.left.left = new Node(1); root.left.right = new Node(3); root.right = new Node(12); root.right.left = new Node(9); root.right.right = new Node(21); root.right.right.left = new Node(19); root.right.right.right = new Node(25); console.log(findMaxFork(root k));
Ieșire
21
[Abordare așteptată] Folosind iterația - O(h) Timp și O(1) Spațiu
C++Ideea este să începem de la rădăcină și comparați valoarea acesteia cu k . Dacă valoarea nodului este <= k actualizați valoarea rezultatului la valoarea root și treceți la corect subarborele altfel trece la stânga subarborele. De iterativ aplicând această operație pe toate nodurile putem minimiza spațiul necesar pentru recursiunea stivă.
// C++ code to find the largest value // smaller than or equal to k using recursion #include
// Java code to find the largest value // smaller than or equal to k using recursion class Node { int data; Node left right; Node(int val) { data = val; left = null; right = null; } } class GfG { // function to find max value less than k static int findMaxFork(Node root int k) { int result = -1; // Start from root and keep looking for larger while (root != null) { // If root is smaller go to right side if (root.data <= k) { result = root.data; root = root.right; } // If root is greater go to left side else { root = root.left; } } return result; } public static void main(String[] args) { int k = 24; // creating following BST // // 5 // / // 2 12 // / / // 1 3 9 21 // / // 19 25 Node root = new Node(5); root.left = new Node(2); root.left.left = new Node(1); root.left.right = new Node(3); root.right = new Node(12); root.right.left = new Node(9); root.right.right = new Node(21); root.right.right.left = new Node(19); root.right.right.right = new Node(25); System.out.println(findMaxFork(root k)); } }
# Python code to find the largest value # smaller than or equal to k using recursion class Node: def __init__(self val): self.data = val self.left = None self.right = None # function to find max value less than k def findMaxFork(root k): result = -1 # Start from root and keep looking for larger while root is not None: # If root is smaller go to right side if root.data <= k: result = root.data root = root.right # If root is greater go to left side else: root = root.left return result if __name__ == '__main__': k = 24 # creating following BST # # 5 # / # 2 12 # / / # 1 3 9 21 # / # 19 25 root = Node(5) root.left = Node(2) root.left.left = Node(1) root.left.right = Node(3) root.right = Node(12) root.right.left = Node(9) root.right.right = Node(21) root.right.right.left = Node(19) root.right.right.right = Node(25) print(findMaxFork(root k))
// C# code to find the largest value // smaller than or equal to k using recursion using System; class Node { public int data; public Node left right; public Node(int val) { data = val; left = null; right = null; } } class GfG { // function to find max value less than k static int FindMaxFork(Node root int k) { int result = -1; // Start from root and keep looking for larger while (root != null) { // If root is smaller go to right side if (root.data <= k) { result = root.data; root = root.right; } // If root is greater go to left side else { root = root.left; } } return result; } static void Main() { int k = 24; // creating following BST // // 5 // / // 2 12 // / / // 1 3 9 21 // / // 19 25 Node root = new Node(5); root.left = new Node(2); root.left.left = new Node(1); root.left.right = new Node(3); root.right = new Node(12); root.right.left = new Node(9); root.right.right = new Node(21); root.right.right.left = new Node(19); root.right.right.right = new Node(25); Console.WriteLine(FindMaxFork(root k)); } }
// JavaScript code to find the largest value // smaller than or equal to k using recursion class Node { constructor(val) { this.data = val; this.left = null; this.right = null; } } // function to find max value less than k function findMaxFork(root k) { let result = -1; // Start from root and keep looking for larger while (root !== null) { // If root is smaller go to right side if (root.data <= k) { result = root.data; root = root.right; } // If root is greater go to left side else { root = root.left; } } return result; } let k = 24; // creating following BST // // 5 // / // 2 12 // / / // 1 3 9 21 // / // 19 25 let root = new Node(5); root.left = new Node(2); root.left.left = new Node(1); root.left.right = new Node(3); root.right = new Node(12); root.right.left = new Node(9); root.right.right = new Node(21); root.right.right.left = new Node(19); root.right.right.right = new Node(25); console.log(findMaxFork(root k));
Ieșire
21Creați un test


