A Graficul aciclic direcționat , adesea prescurtat ca ZI , este un concept fundamental în teoria grafurilor. DAG-urile sunt folosite pentru a arăta cum lucrurile sunt legate sau depind unele de altele într-un mod clar și organizat. În acest articol, vom afla despre Graficul aciclic direcționat , proprietățile sale și aplicarea în viața reală.

Graficul aciclic direcționat

Ce este un grafic aciclic direcționat?

A Graficul aciclic direcționat (DAG) este un grafic direcționat care nu conține niciun ciclu.

Graficul de mai jos reprezintă un grafic aciclic direcționat (DAG):

Graficul aciclic direct

Semnificația graficului aciclic direcționat:

Graficul aciclic direcționat are două caracteristici importante:

• Marginea Dirijată s:În graficul aciclic direcționat, fiecare muchie are o direcție, adică merge de la un vârf (nod) la altul. Această direcție semnifică a Sens unic relație sau dependență între noduri.
• Aciclic: Termenul aciclic indică faptul că nu există cicluri sau bucle închise în grafic. Cu alte cuvinte, nu puteți parcurge o secvență de muchii direcționate și să vă întoarceți la același nod, urmând direcțiile marginilor. Formarea de cicluri este interzisă în ZI. Prin urmare, această caracteristică este esențială.

Graficul aciclic direcționat

Proprietăți ale graficului aciclic direcționat DAG:

Graficul aciclic direcționat (DAG) are proprietăți diferite care le fac utilizabile în problemele grafice.

Există următoarele proprietăți ale graficului aciclic direcționat (DAG):

• Relația de accesibilitate: În DAG, putem determina dacă există o relație de accesibilitate între două noduri. Se spune că nodul A este accesibil de la nodul B dacă există o cale direcționată care începe la nodul B și se termină la nodul A. Aceasta implică faptul că puteți urma direcția muchiilor din grafic pentru a ajunge de la B la A.
• Închidere tranzitivă: Închiderea tranzitivă a unui graf direcționat este un nou graf care reprezintă toate relațiile directe și indirecte sau conexiunile dintre nodurile din graficul original. Cu alte cuvinte, vă spune la ce noduri se poate ajunge de la alte noduri urmând una sau mai multe margini direcționate.

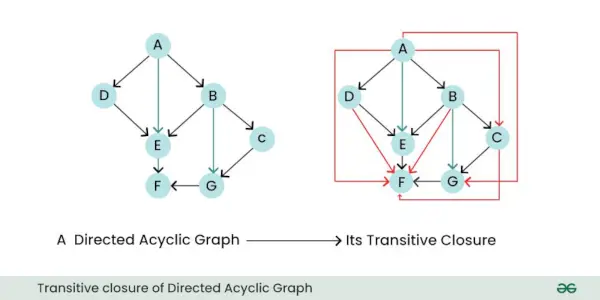
Închiderea tranzitivă a graficului aciclic direcționat

• Reducere tranzitivă: Reducerea tranzitivă a unui graf direcționat este un graf nou care păstrează doar relațiile esențiale, directe dintre noduri, îndepărtând în același timp orice margini indirecte inutile. În esență, simplifică graficul eliminând muchiile care pot fi deduse din muchiile rămase.

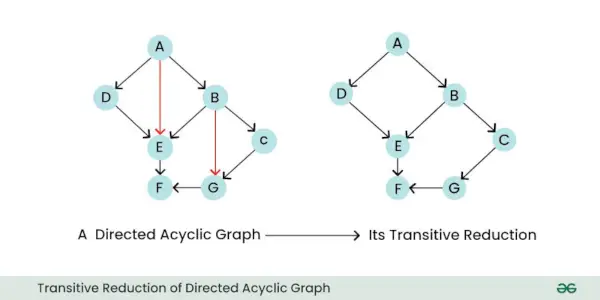
Reducerea tranzitivă a grafului aciclic direcționat

• Ordinea topologică: Un DAG poate fi sortat topologic, ceea ce înseamnă că îi puteți ordona liniar nodurile în așa fel încât pentru toate muchiile, nodul de pornire al muchiei să apară mai devreme în secvență. Această proprietate este utilă pentru sarcini precum programarea și rezolvarea dependențelor.

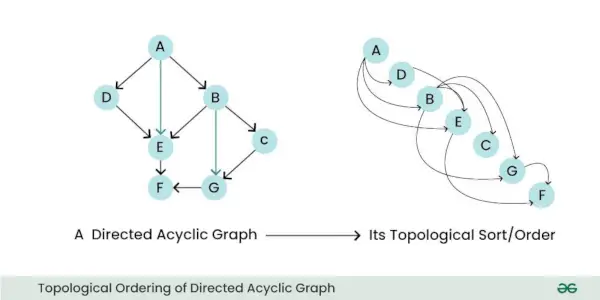
Ordonarea topologică a graficului aciclic direcționat

Aplicații practice ale DAG:

• Analiza fluxului de date: În proiectarea și optimizarea compilatorului, DAG-urile sunt folosite pentru a reprezenta fluxul de date în cadrul unui program. Acest lucru ajută la optimizarea codului prin identificarea calculelor redundante și a codului mort. DAG-urile sunt, de asemenea, folosite pentru a reprezenta structura blocuri de bază în proiectarea compilatorului.

• Programarea sarcinilor: DAG-urile sunt utilizate în managementul proiectelor și în planificarea lucrărilor. Fiecare sarcină sau job este reprezentat ca un nod în DAG, cu margini direcționate indicând dependențe. Natura aciclică a DAG asigură că sarcinile sunt programate într-o ordine logică, prevenind dependențele circulare.

Un grafic aciclic direcționat ponderat poate fi utilizat pentru a reprezenta o problemă de planificare. Să luăm exemplul unei probleme de programare a sarcinilor. Aici, un vârf poate reprezenta sarcina, iar greutatea acestuia poate reprezenta dimensiunea calculului sarcinii. În mod similar, o margine poate reprezenta comunicarea între două sarcini, iar greutatea sa poate reprezenta costul comunicării:

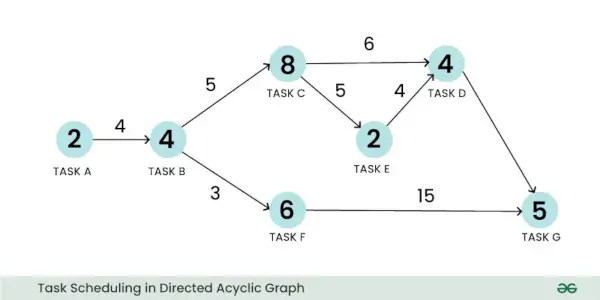
Programarea sarcinilor în graficul aciclic direcționat

Concluzie:

În rezumat, graficele aciclice direcționate sunt un concept fundamental al teoriei grafurilor cu numeroase aplicații practice. DAG-urile joacă un rol crucial în programarea sarcinilor, analiza fluxului de date, rezoluția dependenței și diverse alte domenii ale informaticii și ingineriei. Acestea ajută la optimizarea proceselor, la gestionarea dependențelor și la asigurarea executării eficiente a sarcinilor sau joburilor.