Înălțimea sau adâncimea unui arbore binar poate fi definită ca numărul maxim sau cel mai mare de muchii de la un nod frunză la nodul rădăcină sau nodul rădăcină la nodul frunză. Nodul rădăcină va fi la nivelul zero, ceea ce înseamnă că dacă nodul rădăcină nu are niciunul dintre nodurile secundare conectate la el, atunci se spune că înălțimea sau adâncimea arborelui binar este zero.
Să luăm un exemplu pentru o mai bună înțelegere a înălțimii arborelui binar.
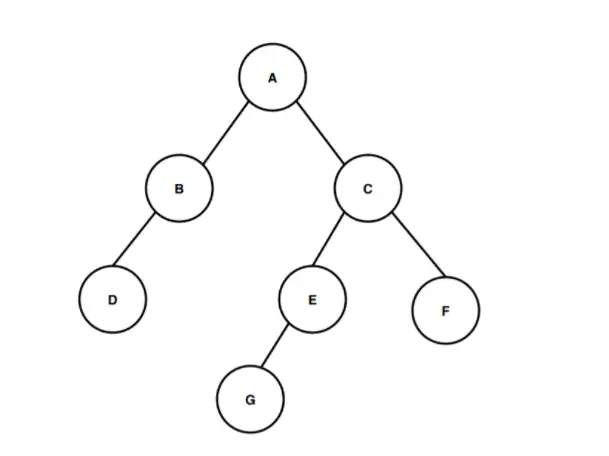
În imaginea de mai sus, avem un arbore binar pornind de la nodul rădăcină numit A. Nodul rădăcină A are două noduri copil B și C drept copil stâng și, respectiv, copil drept. Și, în mod similar, nodul copil stâng B are un singur nod copil stâng numit D și nodul copil drept C are două noduri copil E și F din care nodul E are nodul G ca singurul copil stâng.
obiect la jsonobject java
Acum să calculăm înălțimea acestui arbore binar. Numărați numărul de margini începând de la nodul rădăcină până la cel mai adânc nod de frunză pentru a calcula înălțimea arborelui binar. Cel mai adânc nod care este prezent în acest arbore binar este nodul G. Deci, pentru calcularea înălțimii sau adâncimii acestui arbore binar trebuie să calculăm numărul de muchii dintre nodul rădăcină și cel mai adânc nod G. Prima margine este de la nodul A la nodul C, a doua muchie este de la nodul C la nodul E și a treia muchie este de la nodul E la nodul G. Deci, pentru parcurgerea de la nodul rădăcină A la cel mai adânc nod G există trei muchii. , deci înălțimea sau adâncimea arborelui binar este 3. Calea pe care am urmat-o pentru a trece de la rădăcină la cel mai adânc nod al frunzei este A > C > E > G și această cale acoperă trei margini în timpul traversării, de aceea conform la definiția înălțimii arborelui binar, înălțimea acestui arbore binar este de 3.
Modalități de a găsi înălțimea arborelui binar
Acum, să scriem cod pentru a găsi înălțimea unui arbore binar. Există două moduri de a găsi înălțimea arborelui binar. Unul este metoda recursivă iar celălalt este metoda nerecursivă care va folosi structura de date Queue pentru a calcula înălțimea arborelui binar.
Calea recursiva
Mai întâi, să vedem modul recursiv de a găsi înălțimea arborelui binar.
Cod:
// Java program to create and to find the height of a binary tree by recursive way // util package is imported to use classes like Queue and LinkedList import java.util.*; // A class named Node is created representing a single node of a binary tree class Node{ // The class Node has three class variables named key and left and right of int type and Node type respectively. // the key variable holds the actual value that is assigned to that node of the binary tree int key; // left and right variables that are of Node type will be used to store the left and right child nodes of the parent of the binary tree Node left, right; // a parameterized constructor is created to create and add data to the node at the same time. public Node(int item) { key = item; left = right = null; } } // end of node class definition // A public class named BinaryTree is created having two constructors and methods to print the binary tree level-wise. class BinaryTree{ // A static variable named root_node is created that will represent the node of the binary tree static Node root_node; // A parametrized constructor of the BinaryTree class is written having the key as a parameter BinaryTree(int key) { // here we are constructing a new node and assigning it to the root node root_node = new Node(key); } BinaryTree() { root_node = null; } // a public static function named print tree is created to print all the nodes in the tree level-wise starting from the root node public static void printTree() { int h = height(root_node); int i; for (i=1; i<=h; i++){ printcurrentlevel(root_node, i); system.out.println(); } a public static function named height is created to fund the of binary tree starting from root node deepest leaf that present in passed as parameter called recursively until returned null find int height(node root){ then will be zero if (root="=" null) return 0; else { * compute each subtree lheight="height(root.left);" rheight="height(root.right);" use larger one both sub trees calcualted and which higher used. (lheight> rheight) return(lheight+1); else return(rheight+1); } } // a Public static function named printCurrentLevel is created to print al the nodes that are present in that level // this function is called repeatedly for each level of the binary tree to print all the nodes in that particular level public static void printCurrentLevel (Node root ,int level) { if (root == null) return; if (level == 1) System.out.print(root.key + ' '); else if (level > 1) { printCurrentLevel(root.left, level-1); printCurrentLevel(root.right, level-1); } } //the main function is created to create an object of the BinaryTree class and call the printTree method to level-wise print the nodes of the binary tree and the height method to find the height of the binary tree public static void main(String[] args){ // first of all we have created an Object of the BinaryTree class that will represent the binary tree BinaryTree tree = new BinaryTree(); // now a new node with the value as 150 is added as the root node to the Binary Tree tree.root_node = new Node(150); // now a new node with the value 250 is added as a left child to the root node tree.root_node.left = new Node(250); // now a new node with the value 270 is added as a right child to the root node tree.root_node.right = new Node(270); // now a new node with the value 320 is added as a left child to the left node of the previous level node tree.root_node.left.left = new Node(320); // now a new node with the value 350 is added as a right child to the right node of the previous level node tree.root_node.left.right = new Node(350); /* 150 / 250 270 / / 320 350 null null */ System.out.println('Printing the nodes of tree level wise :'); System.out.println('Level order traversal : '); tree.printTree(); // height of the binary tree is calculated bypassing the root as parameter to the height() function. int h = tree.height(tree.root_node) System.out.println('The height of the Binary tree is : ' + h ); } } // end of the BinaryTree class </=h;> Ieșire: Rezultatul codului de mai sus este:
Printing the nodes of tree level wise: Level order traversal: (level 0) 150 (level 1) 250 270 (level 2) 320 350 The height of the Binary tree is: 2
Într-un mod recursiv, am numit înălţime() funcţionează în mod repetat pentru a găsi înălţimea arborelui binar. Nodul rădăcină al arborelui binar este transmis ca parametru funcției height(). Funcția height() calculează înălțimea ambilor subarbori ai nodului rădăcină și care dintre ambele înălțimi este mai mare este considerată ca înălțimea arborelui binar.
Calea non-recursivă
Acum să vedem modalitatea nerecursivă de a găsi înălțimea arborelui binar.
Cod:
schimba numele directorului linux
// A C++ program to create and to find the height of a binary tree by non recursive way // iostream header file is included to use the cin and cout objects of the istream and ostream classes respectively #include #include using namespace std; // A struct named Node is created representing a single node of a binary tree struct Node { // The struct Node has three variables named key and left and right of int type and Node type respectively. // the key variable holds the actual value that is assigned to that node of the binary tree int key; // left and right variables that are of Node type will be used to store the left and right child nodes of the parent of the binary tree struct Node* left, *right; }; // A Function named newNode is created to add a new node to the binary tree, the newNode function has one parameter of integer type named key that will represent the value that particular new node will be storing Node* newNode(int key) { Node* temp = new Node; temp->key = key; temp->left = temp->right = NULL; return (temp); } // A function named height is created to find the height of the binary tree with non recursive way // The parameter to the height function is the root node of the binary tree that will be present at level zero // In the height function the nodes of the binary tree are added into the Queue data structure and the depth variable is incremented until // the NULL node is encountered while traversing the nodes of the binary tree stored in the Queue data structure. int height(struct Node* root){ //Initialising a variable to count the //height of tree int depth = 0; queueq; //Pushing first level element along with NULL q.push(root); q.push(NULL); while(!q.empty()){ Node* temp = q.front(); q.pop(); //When NULL encountered, increment the value if(temp == NULL){ depth++; } //If NULL not encountered, keep moving if(temp != NULL){ if(temp->left){ q.push(temp->left); } if(temp->right){ q.push(temp->right); } } //If queue still have elements left, //push NULL again to the queue. else if(!q.empty()){ q.push(NULL); } } return depth; } // Start of the main function int main() { // first of all we have created an Object of the struct Node that will represent the binary tree // the value of the root node is 10 Node *root = newNode(10); // now a new node with the value 20 is added as a left child to the root node root->left = newNode(20); // now a new node with the value 30 is added as a right child to the root node root->right = newNode(30); // now a new node with the value 40 is added as a left child to the left node of the previous level node root->left->left = newNode(40); // now a new node with the value 50 is added as a right child to the left node of the previous level node root->left->right = newNode(50); /* 10 / 20 30 / / 40 50 null null */ cout<<'the height(depth) of tree is: '<<height(root); cout<<endl; } end the main function < pre> <p> <strong>Output:</strong> </p> <pre> The Height(Depth) of the tree is: 2 </pre> <p>In this approach, we have used a non recursive way to find the depth of the binary tree. To find the height of the binary tree, we have written a function named height that will require a parameter of Node type (that means the root of the binary tree whose height needs to be calculated). The root of the binary tree is present at level zero, which means the height or depth of the root is zero.</p> <p>In the non recursive approach, we use the Queue Data Structure to find the depth of the binary tree. The nodes of the binary tree for which we want to find the depth are added to the Queue data structure with the help of an enqueue operation to which the node of the binary tree is passed as a parameter to this function.</p> <p>Once all the nodes are added to the queue, the nodes added in the queue are removed by calling the dequeue function that will keep on removing one element from the queue until the null node of the binary tree is encountered. Each time a node of the binary tree from the queue is removed, the depth variable representing the depth of the binary tree is incremented by one. And in the end, the value of the depth variable will represent the final depth of the binary tree.</p> <hr></'the> În această abordare, am folosit o modalitate nerecursivă de a găsi adâncimea arborelui binar. Pentru a găsi înălțimea arborelui binar, am scris o funcție numită înălțime care va necesita un parametru de tip Node (adică rădăcina arborelui binar a cărui înălțime trebuie calculată). Rădăcina arborelui binar este prezentă la nivelul zero, ceea ce înseamnă că înălțimea sau adâncimea rădăcinii este zero.
În abordarea nerecursivă, folosim Structura de date a cozii pentru a găsi adâncimea arborelui binar. Nodurile arborelui binar pentru care dorim să aflăm adâncimea sunt adăugate structurii de date Queue cu ajutorul unei operații de coadă la care nodul arborelui binar este trecut ca parametru acestei funcție.
Odată ce toate nodurile sunt adăugate în coadă, nodurile adăugate în coadă sunt eliminate prin apelarea funcției de scoatere din coadă care va continua să scoată un element din coadă până când este întâlnit nodul nul al arborelui binar. De fiecare dată când un nod al arborelui binar din coadă este îndepărtat, variabila de adâncime care reprezintă adâncimea arborelui binar este incrementată cu unu. Și în final, valoarea variabilei de adâncime va reprezenta adâncimea finală a arborelui binar.
