Metoda lacomă este una dintre strategiile precum Împărțiți și cuceriți folosite pentru a rezolva problemele. Această metodă este utilizată pentru rezolvarea problemelor de optimizare. O problemă de optimizare este o problemă care necesită rezultate maxime sau minime. Să înțelegem prin câțiva termeni.
Metoda Greedy este cea mai simplă și directă abordare. Nu este un algoritm, ci este o tehnică. Funcția principală a acestei abordări este ca decizia să fie luată pe baza informațiilor disponibile în prezent. Oricare ar fi informațiile actuale prezente, decizia este luată fără a vă face griji cu privire la efectul deciziei curente în viitor.
np.clip
Această tehnică este utilizată practic pentru a determina soluția fezabilă care poate fi sau nu optimă. Soluția fezabilă este o submulțime care satisface criteriile date. Soluția optimă este soluția care este cea mai bună și cea mai favorabilă soluție din submulțiune. În cazul fezabilului, dacă mai multe soluții îndeplinesc criteriile date, atunci acele soluții vor fi considerate ca fiind fezabile, în timp ce soluția optimă este cea mai bună soluție dintre toate soluțiile.
Caracteristicile metodei Greedy
Următoarele sunt caracteristicile unei metode lacome:
- Pentru a construi soluția într-un mod optim, acest algoritm creează două seturi în care un set conține toate elementele alese, iar un alt set conține elementele respinse.
- Un algoritm Greedy face alegeri locale bune în speranța că soluția ar trebui să fie fie fezabilă, fie optimă.
Componentele algoritmului Greedy
Componentele care pot fi utilizate în algoritmul greedy sunt:
fișier csv citiți java
Aplicații ale algoritmului Greedy
- Este folosit pentru a găsi calea cea mai scurtă.
- Este folosit pentru a găsi arborele de acoperire minim folosind algoritmul prim-ului sau algoritmul lui Kruskal.
- Este folosit într-o secvențiere de locuri de muncă cu un termen limită.
- Acest algoritm este folosit și pentru a rezolva problema rucsacului fracționat.
Pseudocod al algoritmului Greedy
Algorithm Greedy (a, n) { Solution : = 0; for i = 0 to n do { x: = select(a); if feasible(solution, x) { Solution: = union(solution , x) } return solution; } } Cel de mai sus este algoritmul lacom. Inițial, soluția este atribuită cu valoare zero. Trecem matricea și numărul de elemente în algoritmul greedy. În bucla for, selectăm elementul unul câte unul și verificăm dacă soluția este fezabilă sau nu. Dacă soluția este fezabilă, atunci realizăm unirea.
Să înțelegem printr-un exemplu.
Să presupunem că există o problemă „P”. Doresc să călătoresc de la A la B, prezentate mai jos:
P: A → B
Problema este că trebuie să călătorim în această călătorie de la A la B. Există diverse soluții pentru a merge de la A la B. Putem merge de la A la B prin mers pe jos, mașină, bicicletă, tren, avion , etc. Există o constrângere în călătorie că trebuie să parcurgem această călătorie în 12 ore. Dacă merg cu trenul sau avionul numai atunci, pot acoperi această distanță în 12 ore. Există multe soluții la această problemă, dar există doar două soluții care satisfac constrângerea.
topologii
Dacă spunem că trebuie să acoperim călătoria la costul minim. Aceasta înseamnă că trebuie să parcurgem această distanță cât mai puțin posibil, așa că această problemă este cunoscută ca o problemă de minimizare. Până acum, avem două soluții fezabile, și anume, una cu trenul și alta pe calea aerului. Deoarece călătoria cu trenul va duce la costul minim, este o soluție optimă. O soluție optimă este, de asemenea, soluția fezabilă, dar oferind cel mai bun rezultat, astfel încât soluția respectivă să fie soluția optimă cu costul minim. Ar fi o singură soluție optimă.
Problema care necesită rezultatul minim sau maxim atunci acea problemă este cunoscută ca o problemă de optimizare. Metoda Greedy este una dintre strategiile folosite pentru rezolvarea problemelor de optimizare.
Dezavantajele utilizării algoritmului Greedy
Algoritmul Greedy ia decizii pe baza informațiilor disponibile în fiecare fază, fără a lua în considerare problema mai largă. Deci, ar putea exista posibilitatea ca soluția lacomă să nu ofere cea mai bună soluție pentru fiecare problemă.
înlocuiește-le pe toate
Urmează alegerea optimă locală în fiecare etapă cu intenția de a găsi optimul global. Să înțelegem printr-un exemplu.
Luați în considerare graficul care este prezentat mai jos:
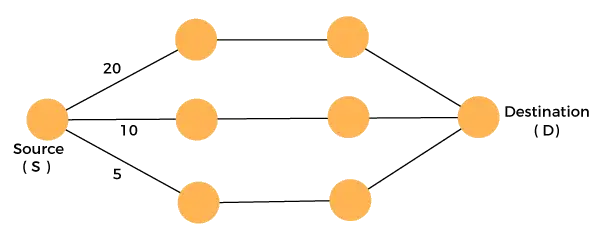
Trebuie să călătorim de la sursă la destinație la costul minim. Deoarece avem trei soluții fezabile având căi de cost ca 10, 20 și 5. 5 este calea costului minim, deci este soluția optimă. Acesta este optimul local și, în acest fel, găsim optimul local în fiecare etapă pentru a calcula soluția optimă globală.
