Algoritmul Ford-Fulkerson este un algoritm utilizat pe scară largă pentru a rezolva problema debitului maxim într-o rețea de flux. Problema debitului maxim implică determinarea cantității maxime de flux care poate fi trimisă de la un vârf sursă la un vârf absorbant într-un grafic ponderat direcționat, supus constrângerilor de capacitate pe margini.

Algoritmul funcționează prin găsirea iterativă a unei căi de creștere, care este o cale de la sursă la chiuvetă în graficul rezidual, adică graficul obținut prin scăderea fluxului de curent din capacitatea fiecărei muchii. Algoritmul crește apoi debitul de-a lungul acestei căi cu cantitatea maximă posibilă, care este capacitatea minimă a marginilor de-a lungul căii.

Problemă:

Dat un grafic care reprezintă o rețea de flux în care fiecare muchie are o capacitate. De asemenea, având în vedere două vârfuri sursă ‘s’ și chiuvetă „t” în grafic, găsiți debitul maxim posibil de la s la t cu următoarele constrângeri:

• Debitul pe o margine nu depășește capacitatea dată a marginii.
• Fluxul de intrare este egal cu fluxul de ieșire pentru fiecare vârf, cu excepția lui s și t.

De exemplu, luați în considerare următorul grafic din cartea CLRS.

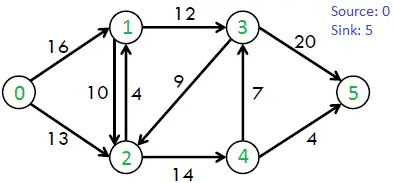
Debitul maxim posibil din graficul de mai sus este 23.

Condiție preliminară: Introducere problemei fluxului maxim

Algoritmul Ford-Fulkerson

Următoarea este o idee simplă a algoritmului Ford-Fulkerson:

1. Începeți cu debitul inițial ca 0.
2. Deși există o cale de creștere de la sursă la chiuvetă:
   • Găsiți o cale de creștere utilizând orice algoritm de găsire a căii, cum ar fi căutarea pe lățimea întâi sau căutarea pe adâncime.
   • Determinați cantitatea de flux care poate fi trimisă de-a lungul căii de creștere, care este capacitatea reziduală minimă de-a lungul marginilor căii.
   • Creșteți debitul de-a lungul căii de creștere cu o cantitate determinată.
3. Reveniți debitul maxim.

Complexitatea timpului: Complexitatea temporală a algoritmului de mai sus este O(max_flow * E). Executăm o buclă în timp ce există o cale de creștere. În cel mai rău caz, putem adăuga 1 unitate de flux în fiecare iterație. Prin urmare, complexitatea timpului devine O(max_flow * E).

Cum se implementează algoritmul simplu de mai sus?
Să definim mai întâi conceptul de grafic rezidual care este necesar pentru înțelegerea implementării.

vârsta mia khalifa

Graficul rezidual al unei rețele de flux este un grafic care indică un flux suplimentar posibil. Dacă există o cale de la sursă la chiuvetă în graficul rezidual, atunci este posibil să adăugați flux. Fiecare muchie a unui grafic rezidual are o valoare numită capacitate reziduala care este egală cu capacitatea inițială a marginii minus fluxul de curent. Capacitatea reziduală este practic capacitatea curentă a marginii.

Să vorbim acum despre detaliile implementării. Capacitatea reziduală este 0 dacă nu există muchie între două vârfuri ale graficului rezidual. Putem inițializa graficul rezidual ca grafic original deoarece nu există un flux inițial și capacitatea reziduală inițială este egală cu capacitatea inițială. Pentru a găsi o cale de creștere, putem face fie un BFS, fie un DFS al graficului rezidual. Am folosit BFS în implementarea de mai jos. Folosind BFS, putem afla dacă există o cale de la sursă la chiuvetă. BFS construiește și matricea părinte[]. Folosind matricea părinte[], traversăm calea găsită și găsim flux posibil prin această cale prin găsirea capacității reziduale minime de-a lungul căii. Mai târziu, adăugăm fluxul căii găsite la fluxul general.

Important este că trebuie să actualizăm capacitățile reziduale din graficul rezidual. Scădem fluxul traseului din toate muchiile de-a lungul căii și adăugăm fluxul căii de-a lungul marginilor inverse. Trebuie să adăugăm fluxul căii de-a lungul marginilor inverse, deoarece mai târziu poate fi necesar să trimitem fluxul în direcția inversă (vezi link-ul următor, de exemplu).

Mai jos este implementarea algoritmului Ford-Fulkerson. Pentru a menține lucrurile simple, graficul este reprezentat ca o matrice 2D.

C++

selectați din mai multe tabele în sql

>

>

Java

> 
    
stivă în java
   
 
     
  
 
    
 
     
     
    
 
 
 
 
 
 # Python program for implementation> # of Ford Fulkerson algorithm> from> collections>import> defaultdict> # This class represents a directed graph> # using adjacency matrix representation> class> Graph:> >def> __init__(>self>, graph):> >self>.graph>=> graph># residual graph> >self>. ROW>=> len>(graph)> ># self.COL = len(gr[0])> >'''Returns true if there is a path from source 's' to sink 't' in> >residual graph. Also fills parent[] to store the path '''> >def> BFS(>self>, s, t, parent):> ># Mark all the vertices as not visited> >visited>=> [>False>]>*>(>self>.ROW)> ># Create a queue for BFS> >queue>=> []> ># Mark the source node as visited and enqueue it> >queue.append(s)> >visited[s]>=> True> ># Standard BFS Loop> >while> queue:> ># Dequeue a vertex from queue and print it> >u>=> queue.pop(>0>)> ># Get all adjacent vertices of the dequeued vertex u> ># If a adjacent has not been visited, then mark it> ># visited and enqueue it> >for> ind, val>in> enumerate>(>self>.graph[u]):> >if> visited[ind]>=>=> False> and> val>>>>:> ># If we find a connection to the sink node,> ># then there is no point in BFS anymore> ># We just have to set its parent and can return true> >queue.append(ind)> >visited[ind]>=> True> >parent[ind]>=> u> >if> ind>=>=> t:> >return> True> ># We didn't reach sink in BFS starting> ># from source, so return false> >return> False> > > ># Returns the maximum flow from s to t in the given graph> >def> FordFulkerson(>self>, source, sink):> ># This array is filled by BFS and to store path> >parent>=> [>->1>]>*>(>self>.ROW)> >max_flow>=> 0> # There is no flow initially> ># Augment the flow while there is path from source to sink> >while> self>.BFS(source, sink, parent) :> ># Find minimum residual capacity of the edges along the> ># path filled by BFS. Or we can say find the maximum flow> ># through the path found.> >path_flow>=> float>(>'Inf'>)> >s>=> sink> >while>(s !>=> source):> >path_flow>=> min> (path_flow,>self>.graph[parent[s]][s])> >s>=> parent[s]> ># Add path flow to overall flow> >max_flow>+>=> path_flow> ># update residual capacities of the edges and reverse edges> ># along the path> >v>=> sink> >while>(v !>=> source):> >u>=> parent[v]> >self>.graph[u][v]>->=> path_flow> >self>.graph[v][u]>+>=> path_flow> >v>=> parent[v]> >return> max_flow> > # Create a graph given in the above diagram> graph>=> [[>0>,>16>,>13>,>0>,>0>,>0>],> >[>0>,>0>,>10>,>12>,>0>,>0>],> >[>0>,>4>,>0>,>0>,>14>,>0>],> >[>0>,>0>,>9>,>0>,>0>,>20>],> >[>0>,>0>,>0>,>7>,>0>,>4>],> >[>0>,>0>,>0>,>0>,>0>,>0>]]> g>=> Graph(graph)> source>=> 0>; sink>=> 5> > print> (>'The maximum possible flow is %d '> %> g.FordFulkerson(source, sink))> # This code is contributed by Neelam Yadav> 
 
 
 
 
    
 
>
 
knn
    
 
>
 
 
C#
    
 
     
  
 
    
 
     
     
    
 
 
 
 
 
 // C# program for implementation> // of Ford Fulkerson algorithm> using> System;> using> System.Collections.Generic;> public> class> MaxFlow {> >static> readonly> int> V = 6;>// Number of vertices in> >// graph> >/* Returns true if there is a path> >from source 's' to sink 't' in residual> >graph. Also fills parent[] to store the> >path */> >bool> bfs(>int>[, ] rGraph,>int> s,>int> t,>int>[] parent)> >{> >// Create a visited array and mark> >// all vertices as not visited> >bool>[] visited =>new> bool>[V];> >for> (>int> i = 0; i   visited[i] = false;  // Create a queue, enqueue source vertex and mark  // source vertex as visited  List coada = lista noua ();  coada.Adaugă(i);  vizitat[s] = adevărat;  părinte[i] = -1;  // Buclă BFS standard while (coadă.Număr != 0) { int u = coadă[0];  coada.RemoveAt(0);  pentru (int v = 0; v if (visited[v] == false && rGraph[u, v]> 0) { // Dacă găsim o conexiune la nodul sink //, atunci nu există niciun punct în BFS / / mai trebuie doar să-i setăm părintele // și poate returna true if (v == t) { parent[v] = u } coadă.Add(v] = u; v] = true; } } } // Nu am ajuns la sink în BFS pornind de la sursă, // returnează false return false } // Returnează fluxul maxim // de la s la t în graficul dat int fordFulkerson; (int[, ] graph, int s, int t) { int u, v // Creați un grafic rezidual și completați // graficul rezidual cu // capacități date în graficul original ca // capacități reziduale în graficul rezidual /; / Grafic rezidual unde rGraph[i,j] // indică capacitatea reziduală a // muchiei de la i la j (dacă există o // muchie. Dacă rGraph[i,j] este 0, atunci // nu există) int [, ] rGraph = new int[V, V] pentru (u = 0; u for (v = 0; v rGraph[u, v] = graph[u, v]; // Această matrice este completată de BFS și a stoca calea int[] parent = new int[V];  int max_flow = 0; // Inițial nu există flux // Mărește fluxul în timp ce există o cale de la sursă // la scufundare în timp ce (bfs(rGraph, s, t, parent)) { // Găsiți capacitatea reziduală minimă a marginilor // de-a lungul căii completat de BFS. Sau putem spune // găsiți debitul maxim prin calea găsită.  int path_flow = int.MaxValue;  pentru (v = t; v != s; v = părinte[v]) { u = părinte[v];  path_flow = Math.Min(path_flow, rGraph[u, v]);  } // actualizează capacitățile reziduale ale muchiilor și // inversează muchiile de-a lungul căii pentru (v = t; v != s; v = părinte[v]) { u = părinte[v];  rGraph[u, v] -= path_flow;  rGraph[v, u] += path_flow;  } // Adăugați fluxul de cale la fluxul general max_flow += path_flow;  } // Returnează fluxul general return max_flow;  } // Cod driver public static void Main() { // Să creăm un grafic prezentat în exemplul de mai sus int[, ] graph = new int[, ] { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 }, { 0, 4, 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 }, { 0, 0, 0, 7 , 0, 4 }, { 0, 0, 0, 0, 0, 0 } };  MaxFlow m = nou MaxFlow();  Console.WriteLine('Debitul maxim posibil este ' + m.fordFulkerson(graph, 0, 5));  } } /* Acest cod a contribuit de PrinciRaj1992 */>
 
 
 
 
    
 
>
 
    
 
>
 
 
Javascript
    
 
     
  
 
    
 
     
     
    
 
 
 
 
 
 > // Javascript program for implementation of Ford> // Fulkerson algorithm> // Number of vertices in graph> let V = 6;> // Returns true if there is a path from source> // 's' to sink 't' in residual graph. Also> // fills parent[] to store the path> function> bfs(rGraph, s, t, parent)> {> > >// Create a visited array and mark all> >// vertices as not visited> >let visited =>new> Array(V);> >for>(let i = 0; i   visited[i] = false;  // Create a queue, enqueue source vertex  // and mark source vertex as visited  let queue = [];  queue.push(s);  visited[s] = true;  parent[s] = -1;  // Standard BFS Loop  while (queue.length != 0)  {  let u = queue.shift();  for(let v = 0; v   {  if (visited[v] == false &&   rGraph[u][v]>0) { // Dacă găsim o conexiune la nodul receptor //, atunci nu mai există niciun punct în BFS // Trebuie doar să-i setăm părintele // și putem returna adevărat dacă (v == t) { părinte[ v] = u;  returnează adevărat;  } coada.push(v);  părinte[v] = u;  vizitat[v] = adevărat;  } } } // Nu am ajuns la sink în BFS pornind // de la sursă, deci returnăm false return false; } // Returnează debitul maxim de la s la t în // funcția grafică dată fordFulkerson(graph, s, t) { let u, v;    // Creați un grafic rezidual și completați // graficul rezidual cu capacități date // în graficul original ca reziduale // capacități în graficul rezidual // Graficul rezidual unde rGraph[i][j] // indică capacitatea reziduală a muchiei // / de la i la j (dacă există o muchie. // Dacă rGraph[i][j] este 0, atunci există // nu) fie rGraph = new Array(V);  for(u = 0; u { rGraph[u] = new Array(V); for(v = 0; v rGraph[u][v] = graph[u][v]; } // Această matrice este completată de BFS și pentru a stoca calea let parent = new Array(V // Nu există flux inițial let max_flow = 0 // Mărește fluxul în timp ce // există cale de la sursă la sink while (bfs(rGraph, s, t); , parent)) { // Găsiți capacitatea reziduală minimă a marginilor // de-a lungul căii umplute de BFS Sau putem spune // găsiți fluxul maxim lat path_flow = Number.MAX_VALUE; ; v != s; v = parent[v]) { u = path_flow = Math.min(path_flow, rGraph[u][v] } // Actualizare capacități reziduale și // margini inverse de-a lungul căii pentru(v = t; v != s; v = părinte[v]) { u = părinte[v]; = path_flow } // Adăugați fluxul de cale la fluxul general max_flow += fluxul de cale generală } // Codul driverului // Să creăm un grafic prezentat în exemplul de mai sus; , 16, 13, 0, 0, 0 ], [ 0, 0, 10, 12, 0, 0 ], [ 0, 4, 0, 0, 14, 0 ], [ 0, 0, 9, 0, 0 , 20 ], [ 0, 0, 0, 7, 0, 4 ], [ 0, 0, 0, 0, 0, 0 ] ]; document.write('Debitul maxim posibil este ' + fordFulkerson(graph, 0, 5)); // Acest cod este contribuit de avanitrachhadiya2155>
 
 
 
 
    
 
>
 
    
 
>
 
care este cazul în sql
  Ieșire  
 
The maximum possible flow is 23>
 
  Complexitatea timpului: O(|V| * E^2) , unde E este numărul de muchii și V este numărul de vârfuri.
 
  Complexitatea spațiului: O(V), pe măsură ce am creat coada.
 
Implementarea de mai sus a algoritmului Ford Fulkerson este numită   Algoritmul Edmonds-Karp   . Ideea lui Edmonds-Karp este de a folosi BFS în implementarea Ford Fulkerson, deoarece BFS alege întotdeauna o cale cu un număr minim de muchii. Când se utilizează BFS, complexitatea timpului în cel mai rău caz poate fi redusă la O(VE2). Implementarea de mai sus utilizează reprezentarea matricei de adiacență, deși BFS ia O(V2), complexitatea de timp a implementării de mai sus este O(EV3) (A se vedea Cartea CLRS pentru dovada complexității timpului)
 
Aceasta este o problemă importantă, deoarece apare în multe situații practice. Exemplele includ, maximizarea transportului cu anumite limite de trafic, maximizarea fluxului de pachete în rețelele de calculatoare. 
Algoritmul lui Dinc pentru Max-Flow.
 
  Exercițiu:   
Modificați implementarea de mai sus, astfel încât să ruleze în O(VE2) timp.