logo

TechCodeview

Algoritmul Floyd Warshall

The Algoritmul Floyd-Warshall , numit după creatorii săi Robert Floyd și Stephen Warshall , este un algoritm fundamental în informatică și teoria grafurilor. Este folosit pentru a găsi cele mai scurte căi între toate perechile de noduri dintr-un grafic ponderat. Acest algoritm este foarte eficient și poate gestiona grafice cu ambele pozitiv si n greutăți de margine negative , ceea ce îl face un instrument versatil pentru rezolvarea unei game largi de probleme de rețea și conectivitate.

Cuprins

Floyd-Warshall-Algoritm-banner



Algoritmul Floyd Warshall:

The Algoritmul Floyd Warshall este un algoritm de calea cea mai scurtă, spre deosebire de toate perechile Dijkstra și Bellman Ford care sunt algoritmi cu calea cea mai scurtă cu o singură sursă. Acest algoritm funcționează atât pentru regizat și ponderat nedirecţionat grafice. Dar, nu funcționează pentru graficele cu cicluri negative (unde suma marginilor dintr-un ciclu este negativă). Urmează Programare dinamică abordare pentru a verifica fiecare cale posibilă care trece prin fiecare nod posibil pentru a calcula distanța cea mai scurtă dintre fiecare pereche de noduri.

o formă completă

Ideea din spatele algoritmului Floyd Warshall:

Să presupunem că avem un grafic G[][] cu ÎN vârfuri din 1 la N . Acum trebuie să evaluăm a shortestPathMatrix[][] unde s hortestPathMatrix[i][j] reprezintă calea cea mai scurtă între vârfuri i și j .

Evident, cea mai scurtă cale între i la j va avea unele k numărul de noduri intermediare. Ideea din spatele algoritmului floyd warshall este de a trata fiecare vârf din 1 la N ca un nod intermediar unul câte unul.

Următoarea figură arată proprietatea optimă a substructurii de mai sus în algoritmul floyd warshall:

Algoritmul Floyd Warshall Algoritmul:

  • Inițializați matricea soluției la fel ca matricea graficului de intrare ca prim pas.
  • Apoi actualizați matricea soluției considerând toate vârfurile ca un vârf intermediar.
  • Ideea este de a alege toate nodurile unul câte unul și de a actualiza toate căile cele mai scurte care includ vârful ales ca vârf intermediar în calea cea mai scurtă.
  • Când alegem numărul de vârf k ca vârf intermediar, am luat deja în considerare vârfurile {0, 1, 2, .. k-1} ca vârfuri intermediare.
  • Pentru fiecare pereche (i, j) dintre vârfurile sursă și respectiv destinație, există două cazuri posibile.
    • k nu este un vârf intermediar pe calea cea mai scurtă de la i la j . Păstrăm valoarea de dist[i][j] așa cum este.
    • k este un vârf intermediar pe calea cea mai scurtă de la i la j . Actualizăm valoarea lui dist[i][j] la fel de dist[i][k] + dist[k][j], dacă dist[i][j]> dist[i][k] + dist[k][j]

Algoritmul Pseudo-Cod al lui Floyd Warshall:>

Pentru k = 0 până la n – 1
Pentru i = 0 până la n – 1
Pentru j = 0 până la n – 1
Distanța[i, j] = min(Distanța[i, j], Distanța[i, k] + Distanța[k, j])

exemplu java salut lume

unde i = Nodul sursă, j = Nodul Destinație, k = Nodul Intermediar

Ilustrație a algoritmului Floyd Warshall:

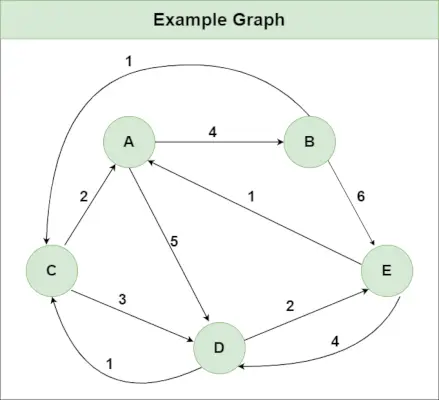
Să presupunem că avem un grafic așa cum se arată în imagine:

dryRun1drawio

Pasul 1 : Inițializați matricea Distanță[][] folosind graficul de intrare astfel încât Distanța[i][j]= greutatea muchiei de la i la j , de asemenea Distanța[i][j] = Infinit dacă nu există margine de la i la j.

pas1 desen

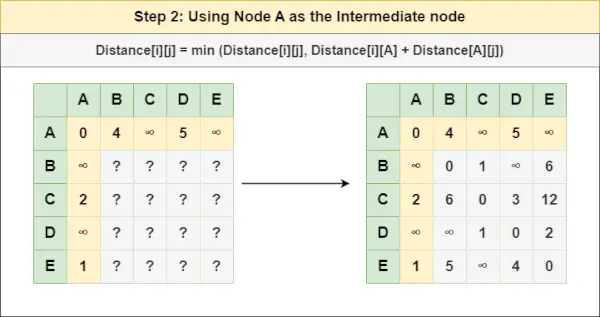
Pasul 2 : Trata nodul A ca nod intermediar și calculați Distanța[][] pentru fiecare pereche de noduri {i,j} folosind formula:

= Distanța[i][j] = minimă (Distanța[i][j], (Distanța de la i la A ) + (Distanța de la A la j))
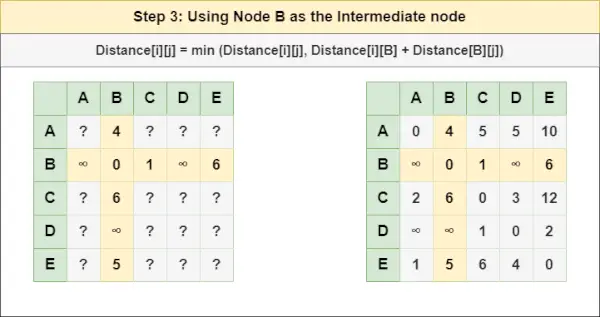
= Distanța[i][j] = minimă (Distanța[i][j], Distanța[i][ A ] + Distanța[ A ][j])

step2drawio

Pasul 3 : Trata nodul B ca nod intermediar și calculați Distanța[][] pentru fiecare pereche de noduri {i,j} folosind formula:

= Distanța[i][j] = minimă (Distanța[i][j], (Distanța de la i la B ) + (Distanța de la B la j))
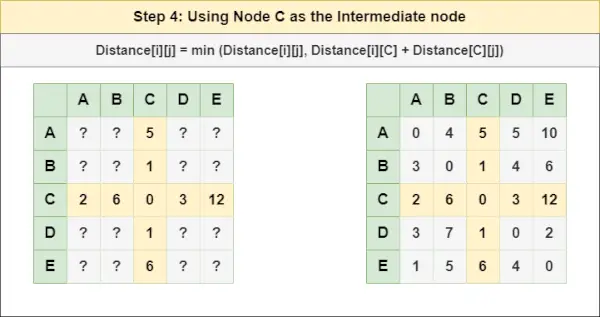
= Distanța[i][j] = minimă (Distanța[i][j], Distanța[i][ B ] + Distanța[ B ][j])

ce este desktop ini
step3drawio

Pasul 4 : Trata nodul C ca nod intermediar și calculați Distanța[][] pentru fiecare pereche de noduri {i,j} folosind formula:

= Distanța[i][j] = minimă (Distanța[i][j], (Distanța de la i la C ) + (Distanța de la C la j))
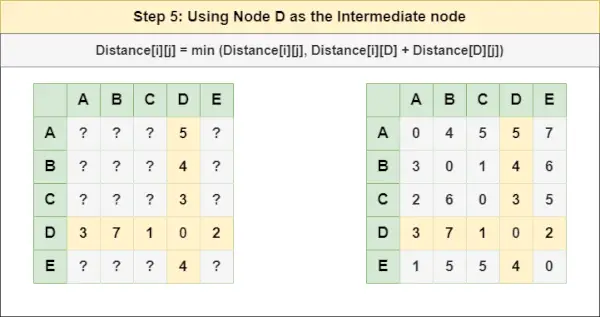
= Distanța[i][j] = minimă (Distanța[i][j], Distanța[i][ C ] + Distanța[ C ][j])

pas4dravio

Pasul 5 : Trata nodul D ca nod intermediar și calculați Distanța[][] pentru fiecare pereche de noduri {i,j} folosind formula:

= Distanța[i][j] = minimă (Distanța[i][j], (Distanța de la i la D ) + (Distanța de la D la j))
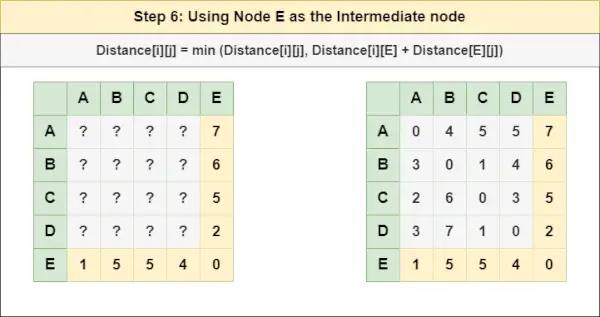
= Distanța[i][j] = minimă (Distanța[i][j], Distanța[i][ D ] + Distanța[ D ][j])

pasul5drawio

Pasul 6 : Trata nodul ȘI ca nod intermediar și calculați Distanța[][] pentru fiecare pereche de noduri {i,j} folosind formula:

= Distanța[i][j] = minimă (Distanța[i][j], (Distanța de la i la ȘI ) + (Distanța de la ȘI la j))
= Distanța[i][j] = minimă (Distanța[i][j], Distanța[i][ ȘI ] + Distanța[ ȘI ][j])

pas6drawio

Pasul 7 : Deoarece toate nodurile au fost tratate ca un nod intermediar, acum putem returna matricea Distanță[][] actualizată ca matrice de răspuns.

căutarea bfs
pasul7drawio
Practică recomandată Încercați!

Mai jos este implementarea abordării de mai sus:

C++ 
// C++ Program for Floyd Warshall Algorithm #include  using namespace std; // Number of vertices in the graph #define V 4 /* Define Infinite as a large enough value.This value will be used for vertices not connected to each other */ #define INF 99999 // A function to print the solution matrix void printSolution(int dist[][V]); // Solves the all-pairs shortest path // problem using Floyd Warshall algorithm void floydWarshall(int dist[][V]) {  int i, j, k;  /* Add all vertices one by one to  the set of intermediate vertices.  --->Înainte de începerea unei iterații, avem cele mai scurte distanțe între toate perechile de vârfuri, astfel încât cele mai scurte distanțe să considere doar vârfurile din mulțimea {0, 1, 2, .. k-1} ca vârfuri intermediare.  ----> După terminarea unei iterații, vârful nr. k se adaugă la mulțimea vârfurilor intermediare și mulțimea devine {0, 1, 2, .. k} */ pentru (k = 0; k< V; k++) {  // Pick all vertices as source one by one  for (i = 0; i < V; i++) {  // Pick all vertices as destination for the  // above picked source  for (j = 0; j < V; j++) {  // If vertex k is on the shortest path from  // i to j, then update the value of  // dist[i][j]  if (dist[i][j]>(dist[i][k] + dist[k][j]) && (dist[k][j] != INF && dist[i][k] != INF)) dist[i][j] = dist[i][k] + dist[k][j];  } } } // Imprimă cea mai scurtă distanță matrice printSolution(dist); } /* O funcție utilitar pentru a tipări soluția */ void printSolution(int dist[][V]) { cout<< 'The following matrix shows the shortest '  'distances'  ' between every pair of vertices 
';  for (int i = 0; i < V; i++) {  for (int j = 0; j < V; j++) {  if (dist[i][j] == INF)  cout << 'INF'  << ' ';  else  cout << dist[i][j] << ' ';  }  cout << endl;  } } // Driver's code int main() {  /* Let us create the following weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int graph[V][V] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, { INF, INF, INF, 0 } };  // Apelul funcției floydWarshall(graph);  întoarce 0; } // Acest cod este contribuit de Mythri J L>>>C(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int graph[V][V] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1}, { INF, INF, INF, 0}};  // Apelul funcției floydWarshall(graph);  întoarce 0; }>>>Java(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int graph[][] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, { INF, INF, INF, 0 } };  AllPairShortestPath a = nou AllPairShortestPath();  // Apel de funcție a.floydWarshall(graph);  } } // A contribuit de Aakash Hasija>>>Python3Înainte de începerea unei iterații, avem cele mai scurte distanțe între toate perechile de vârfuri, astfel încât cele mai scurte distanțe să considere doar vârfurile din mulțimea {0, 1, 2, .. k-1} ca vârfuri intermediare.  ----> După terminarea unei iterații, vârful nr. k se adaugă la mulțimea de vârfuri intermediare și mulțimea devine {0, 1, 2, .. k} ''' pentru k în intervalul (V): # alegeți toate vârfurile ca sursă unul câte unul pentru i în range(V): # Alegeți toate vârfurile ca destinație pentru # sursa aleasă mai sus pentru j în intervalul (V): # Dacă vârful k este pe calea cea mai scurtă de la # i la j, atunci actualizați valoarea dist[i][ j] dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j] ) printSolution(dist) # O funcție utilitar pentru a tipări soluția def printSolution (dist): print('Următoarea matrice arată cele mai scurte distanțe între fiecare pereche de vârfuri') pentru i în interval (V): pentru j în interval (V): if(dist[i][j] == INF): print('%7s' % ('INF'), final=' ') else: print('%7d	' % (dist[i][j]), end=' ') if j == V-1: print() # Codul driverului if __name__ == '__main__': ''' 10 (0)------ ->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 ''' grafic = [[0, 5, INF, 10], [INF, 0, 3, INF], [INF, INF, 0 , 1], [INF, INF, INF, 0] ] # Apelul funcției floydWarshall(graph) # Acest cod este contribuit de Mythri J L>
C# 
// C# program for Floyd Warshall All // Pairs Shortest Path algorithm. using System; public class AllPairShortestPath {  readonly static int INF = 99999, V = 4;  void floydWarshall(int[, ] graph)  {  int[, ] dist = new int[V, V];  int i, j, k;  // Initialize the solution matrix  // same as input graph matrix  // Or we can say the initial  // values of shortest distances  // are based on shortest paths  // considering no intermediate  // vertex  for (i = 0; i < V; i++) {  for (j = 0; j < V; j++) {  dist[i, j] = graph[i, j];  }  }  /* Add all vertices one by one to  the set of intermediate vertices.  --->Înainte de începerea unei iterații, avem cele mai scurte distanțe între toate perechile de vârfuri, astfel încât cele mai scurte distanțe să considere doar vârfurile din mulțimea {0, 1, 2, .. k-1} ca vârfuri intermediare.  ---> După terminarea unei iterații, vârful nr. k se adaugă la mulțimea vârfurilor intermediare și mulțimea devine {0, 1, 2, .. k} */ pentru (k = 0; k< V; k++) {  // Pick all vertices as source  // one by one  for (i = 0; i < V; i++) {  // Pick all vertices as destination  // for the above picked source  for (j = 0; j < V; j++) {  // If vertex k is on the shortest  // path from i to j, then update  // the value of dist[i][j]  if (dist[i, k] + dist[k, j]  < dist[i, j]) {  dist[i, j]  = dist[i, k] + dist[k, j];  }  }  }  }  // Print the shortest distance matrix  printSolution(dist);  }  void printSolution(int[, ] dist)  {  Console.WriteLine(  'Following matrix shows the shortest '  + 'distances between every pair of vertices');  for (int i = 0; i < V; ++i) {  for (int j = 0; j < V; ++j) {  if (dist[i, j] == INF) {  Console.Write('INF ');  }  else {  Console.Write(dist[i, j] + ' ');  }  }  Console.WriteLine();  }  }  // Driver's Code  public static void Main(string[] args)  {  /* Let us create the following  weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int[, ] grafic = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0 , 1 }, { INF, INF, INF, 0 } };  AllPairShortestPath a = nou AllPairShortestPath();  // Apel de funcție a.floydWarshall(graph);  } } // Acest articol este contribuit de // Abdul Mateen Mohammed>
Javascript 
// A JavaScript program for Floyd Warshall All  // Pairs Shortest Path algorithm.  var INF = 99999;  class AllPairShortestPath {  constructor() {  this.V = 4;  }  floydWarshall(graph) {  var dist = Array.from(Array(this.V), () =>nou Array(this.V).fill(0));  var i, j, k;  // Inițializați matricea soluției // la fel ca și matricea graficului de intrare // Sau putem spune că // valorile inițiale ale celor mai scurte distanțe // se bazează pe cele mai scurte căi // luând în considerare niciun punct intermediar // pentru (i = 0; i< this.V; i++) {  for (j = 0; j < this.V; j++) {  dist[i][j] = graph[i][j];  }  }  /* Add all vertices one by one to  the set of intermediate vertices.  --->Înainte de începerea unei iterații, avem cele mai scurte distanțe între toate perechile de vârfuri, astfel încât cele mai scurte distanțe să considere doar vârfurile din mulțimea {0, 1, 2, .. k-1} ca vârfuri intermediare.  ---> După terminarea unei iterații, vârful nr. k se adaugă la mulțimea vârfurilor intermediare și mulțimea devine {0, 1, 2, .. k} */ pentru (k = 0; k< this.V; k++) {  // Pick all vertices as source  // one by one  for (i = 0; i < this.V; i++) {  // Pick all vertices as destination  // for the above picked source  for (j = 0; j < this.V; j++) {  // If vertex k is on the shortest  // path from i to j, then update  // the value of dist[i][j]  if (dist[i][k] + dist[k][j] < dist[i][j]) {  dist[i][j] = dist[i][k] + dist[k][j];  }  }  }  }  // Print the shortest distance matrix  this.printSolution(dist);  }  printSolution(dist) {  document.write(  'Following matrix shows the shortest ' +  'distances between every pair of vertices '  );  for (var i = 0; i < this.V; ++i) {  for (var j = 0; j < this.V; ++j) {  if (dist[i][j] == INF) {  document.write(' INF ');  } else {  document.write('  ' + dist[i][j] + ' ');  }  }  document.write(' ');  }  }  }  // Driver Code  /* Let us create the following  weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ var grafic = [ [0, 5, INF, 10], [INF, 0, 3, INF], [INF, INF, 0, 1] , [INF, INF, INF, 0], ];  var a = nou AllPairShortestPath();  // Imprimă soluția a.floydWarshall(graph);    // Acest cod este contribuit de rdtaank.>>>PHP(3) | /| 5 | |   | | 1 |/ |  (1)------->(2) 3 */ $graph = array(array(0, 5, $INF, 10), array($INF, 0, 3, $INF), array($ INF, $INF, 0, 1), matrice ($INF, $INF, $INF, 0)); // Apelul funcției floydWarshall($graph, $V, $INF); // Acest cod este contribuit de Ryuga ?>>
Ieșire 
The following matrix shows the shortest distances between every pair of vertices 0 5 8 9 INF 0 3 4 INF INF 0 1 INF INF INF 0>

Analiza complexității algoritmului Floyd Warshall:

  • Complexitatea timpului: O(V3), unde V este numărul de vârfuri din grafic și rulăm trei bucle imbricate fiecare cu dimensiunea V
  • Spațiu auxiliar: O(V2), pentru a crea o matrice 2-D pentru a stoca cea mai scurtă distanță pentru fiecare pereche de noduri.

Notă : Programul de mai sus tipărește doar cele mai scurte distanțe. Putem modifica soluția pentru a imprima cele mai scurte căi și prin stocarea informațiilor predecesorului într-o matrice 2D separată.

De ce algoritmul Floyd-Warshall este mai bun pentru graficele dense și nu pentru graficele rare?

Graficul dens : Un grafic în care numărul de muchii este semnificativ mult mai mare decât numărul de vârfuri.
Grafic rar : Un grafic în care numărul de muchii este foarte mic.

Indiferent de câte muchii există în grafic Algoritmul Floyd Warshall rulează pentru O(V3) ori prin urmare este cel mai potrivit pentru Grafice dense . În cazul graficelor rare, Algoritmul lui Johnson este mai potrivit.

  • Cum se detectează ciclul negativ într-un grafic folosind algoritmul Floyd Warshall?
  • Cum este algoritmul Floyd-warshall diferit de algoritmul lui Dijkstra?
  • Cum este algoritmul Floyd-warshall diferit de algoritmul Bellman-Ford?

Aplicații în lumea reală ale algoritmului Floyd-Warshall:

  • În rețelele de calculatoare, algoritmul poate fi folosit pentru a găsi calea cea mai scurtă între toate perechile de noduri dintr-o rețea. Aceasta este denumită ca rutarea rețelei .
  • Conectivitate de zbor În industria aviației pentru a găsi cea mai scurtă cale între aeroporturi.
  • GIS ( Sisteme Informaţionale Geografice ) aplicațiile implică adesea analiza datelor spațiale, cum ar fi rețelele de drumuri, pentru a găsi cele mai scurte căi între locații.
  • algoritmul lui Kleene care este o generalizare a lui Floyd Warshall, poate fi folosită pentru a găsi expresii regulate pentru un limbaj obișnuit.