Arborele expresiei este un arbore folosit pentru a reprezenta diferitele expresii. Structura de date arborescentă este utilizată pentru a reprezenta instrucțiunile expresive. În acest arbore, nodul intern indică întotdeauna operatorii.
- Nodurile frunză denotă întotdeauna operanzii.
- Operațiile sunt întotdeauna efectuate pe acești operanzi.
- Operatorul prezent în adâncimea arborelui are întotdeauna cea mai mare prioritate.
- Operatorul, care nu se află mult la adâncimea în copac, are întotdeauna cea mai mică prioritate în comparație cu operatorii care se află la adâncime.
- Operandul va prezenta întotdeauna la o adâncime a arborelui; prin urmare este considerată cea mai mare prioritate dintre toți operatorii.
- Pe scurt, o putem rezuma deoarece valoarea prezentă la o adâncime a arborelui este la cea mai mare prioritate în comparație cu ceilalți operatori prezenți în vârful arborelui.
- Utilizarea principală a acestor arbori de expresie este că este obișnuit evalua, analiza și modifica diferitele expresii.
- De asemenea, este folosit pentru a afla asociativitatea fiecărui operator din expresie.
- De exemplu, operatorul + este asociatul din stânga și / este asociativul din dreapta.
- Dilema acestei asociativități a fost înlăturată prin utilizarea expresiei arbori.
- Acești arbori de expresii sunt formați folosind o gramatică fără context.
- Am asociat o regulă în gramaticile fără context în fața fiecărei producții gramaticale.
- Aceste reguli sunt cunoscute și ca reguli semantice și, folosind aceste reguli semantice, putem construi cu ușurință arborii de expresie.
- Este una dintre părțile majore ale proiectării compilatorului și aparține fazei de analiză semantică.
- În această analiză semantică, vom folosi traducerile direcționate pe sintaxă și, sub formă de ieșire, vom produce arborele de analiză adnotat.
- Un arbore de analiză adnotat nu este altceva decât o analiză simplă asociată cu atributul tip și cu fiecare regulă de producție.
- Obiectivul principal al utilizării arborilor de expresie este de a face expresii complexe și pot fi evaluate cu ușurință folosind acești arbori de expresie.
- Este imuabil și, odată ce am creat un arbore de expresii, nu îl putem schimba sau modifica în continuare.
- Pentru a face mai multe modificări, este necesar să construiți în întregime noul arbore de expresii.
- De asemenea, este folosit pentru a rezolva evaluarea expresiei postfix, prefix și infix.
Arborele de expresie joacă un rol foarte important în reprezentarea la nivel de limbaj cod sub forma datelor, care sunt stocate în principal în structura arborescentă. Este, de asemenea, folosit în reprezentarea în memorie a lambda expresie. Folosind structura de date arborescentă, putem exprima expresia lambda mai transparent și mai explicit. Este creat mai întâi pentru a converti segmentul de cod în segmentul de date, astfel încât expresia să poată fi evaluată cu ușurință.
Arborele expresiei este un arbore binar în care fiecare nod extern sau frunză corespunde operandului și fiecare nod intern sau părinte corespunde operatorilor, deci de exemplu arborele expresiei pentru 7 + ((1+8)*3) ar fi:
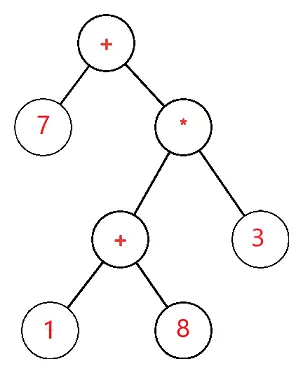
Fie S arborele expresiei
Dacă S nu este nul, atunci
Dacă S.value este un operand, atunci
Returnează valoarea S
x = rezolva (S.stânga)
y = rezolva (S.dreapta)
Returnează calcula (x, y, S.valoare)
Aici, în exemplul de mai sus, arborele expresiei a folosit gramatică fără context.
Avem câteva producții asociate cu unele reguli de producție în această gramatică, cunoscute în principal ca reguli semantice . Putem defini producerea de rezultate din regulile de producție corespunzătoare folosind aceste reguli semantice. Aici am folosit parametrul valoare, care va calcula rezultatul și îl va întoarce la simbolul de început al gramaticii. S.left va calcula copilul din stânga al nodului și, în mod similar, copilul din dreapta al nodului poate fi calculat folosind parametrul S.right.
Utilizarea arborelui de expresie
- Obiectivul principal al utilizării arborilor de expresie este de a face expresii complexe și pot fi evaluate cu ușurință folosind acești arbori de expresie.
- De asemenea, este folosit pentru a afla asociativitatea fiecărui operator din expresie.
- De asemenea, este folosit pentru a rezolva evaluarea expresiei postfix, prefix și infix.
Implementarea unui arbore de expresie
Pentru a implementa arborele de expresie și pentru a-i scrie programul, ni se va cere să folosim o structură de date stivă.
Deoarece știm că stiva se bazează pe principiul LIFO ultimul intrat, primul ieșit, elementul de date introdus recent în stivă a fost scos oricând a fost necesar. Pentru implementarea sa, sunt utilizate principalele două operații ale stivei, push și pop. Folosind operația de push, vom împinge elementul de date în stivă, iar folosind operația pop, vom elimina elementul de date din stivă.
Funcțiile principale ale stivei în implementarea arborelui de expresii:
În primul rând, vom scana expresia dată în sensul stânga la dreapta, apoi vom verifica unul câte unul caracterul identificat,
- Dacă un caracter scanat este un operand, vom aplica operația de push și îl vom împinge în stivă.
- Dacă un caracter scanat este un operator, vom aplica operația pop în el pentru a elimina cele două valori din stivă pentru a le face fiul său, iar după aceea vom împinge înapoi nodul părinte curent în stivă.
Implementarea arborelui de expresie în limbajul de programare C
// C program for expression tree implementation #include #include /* The below structure node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ struct node { char info ; struct node* l ; struct node* r ; struct node* nxt ; }; struct node *head=NULL; /* Helper function that allocates a new node with the given data and NULL left and right pointers. */ struct node* newnode(char data) { struct node* node = (struct node*) malloc ( sizeof ( struct node ) ) ; node->info = data ; node->l = NULL ; node->r = NULL ; node->nxt = NULL ; return ( node ) ; } void Inorder(struct node* node) { if ( node == NULL) return ; else { /* first recur on left child */ Inorder ( node->l ) ; /* then print the data of node */ printf ( '%c ' , node->info ) ; /* now recur on right child */ Inorder ( node->r ) ; } } void push ( struct node* x ) { if ( head == NULL ) head = x ; else { ( x )->nxt = head ; head = x ; } // struct node* temp ; // while ( temp != NULL ) // { // printf ( ' %c ' , temp->info ) ; // temp = temp->nxt ; // } } struct node* pop() { // Poping out the top most [pointed with head] element struct node* n = head ; head = head->nxt ; return n ; } int main() { char t[] = { 'X' , 'Y' , 'Z' , '*' , '+' , 'W' , '/' } ; int n = sizeof(t) / sizeof(t[0]) ; int i ; struct node *p , *q , *s ; for ( i = 0 ; i <n ; i++ ) { if read character is operator then popping two other elements from stack and making a binary tree ( t[i]="=" '+' || '-' '*' ' '^' s="newnode" t [ i ] p="pop()" q="pop()" s->l = q ; s->r = p; push(s); } else { s = newnode ( t [ i ] ) ; push ( s ) ; } } printf ( ' The Inorder Traversal of Expression Tree: ' ) ; Inorder ( s ) ; return 0 ; } </n> Rezultatul programului de mai sus este:
X + Y * Z / W
Implementarea arborelui de expresie în limbajul de programare C++
// C++ program for expression tree #include using namespace std ; /* The below class node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ class node { public: char info ; node* l ; node* r ; node* nxt = NULL ; node ( char c ) { this->info = c ; l = NULL ; r = NULL ; } node() { l = NULL ; r = NULL ; } friend class Stack ; friend class tree ; } ; class Stack { node* head = NULL ; public: void push ( node* ) ; node* pop() ; friend class tree ; } ; class tree { public: void inorder ( node* x ) { // cout<<'tree in inorder traversal is: '<l ) ; cout <info <r } void stack::push( node* x { if ( head="=" null we are inserting here nodes at the top of stack [following lifo principle] else x->nxt = head ; head = x ; } } node* Stack::pop() { // Poping out the top most [ pointed with head ] element node* p = head ; head = head->nxt ; return p ; } int main() { string str = 'XYZ*+W/' ; // If you wish take input from user: //cout << 'Insert Postorder Expression: ' <> s; Stack s ; tree t ; node *p, *q, *re; int n = str.length() ; for ( int i = 0 ; i <n ; i++ ) { if ( str[ i ]="=" '+' || '-' '*' ' '^') re="new" node( str[i] p="s.pop()" q="s.pop()" re->l = q ; re->r = p ; s.push(re) ; } else { re = new node( str[ i ] ) ; s.push(re) ; } } cout << ' The Inorder Traversal of Expression Tree: ' ; t.inorder(re) ; return 0 ; } </n></'tree> Rezultatul programului de mai sus este:
X + Y * Z / W
Implementarea arborelui de expresie în limbajul de programare Java
// Java program for expression tree import java.util.* ; /* The below class node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ class Node { char info ; Node l , r ; public Node(char data) { this.info = data ; l = null ; r = null ; } } public class Main { public static boolean isOperator ( char ch ) { if ( ch == '+' || ch == '-' || ch == '*' || ch == '/' || ch == '^' ) { return true ; } return false ; } public static Node Tree ( String postfix ) { Stack st = new Stack(); Node t1,t2,temp ; for ( int i = 0 ; i <p> <strong>The output of the above program is:</strong> </p> <pre> X + Y * Z / W </pre> <hr> 