Sortarea prin inserție și sortarea prin selecție sunt doi algoritmi de sortare populari, iar diferența lor principală constă în modul în care selectează și plasează elementele într-o secvență sortată.
Sortare selecție:
- În sortarea prin selecție, matricea de intrare este împărțită în două părți: o parte sortată și o parte nesortată.
- Algoritmul găsește în mod repetat elementul minim în partea nesortată și îl schimbă cu elementul din stânga părții nesortate, extinzând astfel partea sortată cu un element.
- Sortarea selecției are o complexitate de timp de O(n^2) în toate cazurile.
Sortare inserare:
- În sortarea prin inserție, matricea de intrare este, de asemenea, împărțită în două părți: o parte sortată și o parte nesortată.
Algoritmul preia un element din partea nesortată și îl plasează în poziția corectă în partea sortată, deplasând elementele mai mari cu o poziție spre dreapta.
Sortarea prin inserție are o complexitate de timp de O(n^2) în cel mai rău caz, dar poate funcționa mai bine pe tablouri parțial sortate, cu o complexitate de timp în cel mai bun caz de O(n).
Principalele diferente: - Sortarea prin selecție scanează partea nesortată pentru a găsi elementul minim, în timp ce sortarea prin inserare scanează partea sortată pentru a găsi poziția corectă pentru a plasa elementul.
Sortarea prin selecție necesită mai puține schimburi decât sortarea prin inserare, dar mai multe comparații.
Sortarea prin inserție este mai eficientă decât sortarea prin selecție atunci când matricea de intrare este sortată parțial sau aproape sortată, în timp ce sortarea prin selecție are rezultate mai bune când matricea este foarte nesortată.
Pe scurt, ambii algoritmi au o complexitate de timp similară, dar metodele lor de selecție și plasare diferă. Alegerea dintre ele depinde de caracteristicile datelor de intrare și de cerințele specifice ale problemei în cauză.
Avantajele sortării prin inserție:
- Simplu și ușor de înțeles și implementat.
- Eficient pentru seturi de date mici sau date aproape sortate.
- Algoritm de sortare in loc, ceea ce înseamnă că nu necesită memorie suplimentară.
- Algoritm de sortare stabil, ceea ce înseamnă că menține ordinea relativă a elementelor egale în matricea de intrare.
Dezavantajele sortării prin inserție:
- Ineficient pentru seturi mari de date sau date ordonate invers, cu o complexitate de timp în cel mai rău caz de O(n^2).
- Sortarea prin inserție are o mulțime de schimburi, ceea ce o poate face încet pe computerele moderne.
Avantajele sortării selecției:
- Simplu și ușor de înțeles și implementat.
- Eficient pentru seturi de date mici sau date aproape sortate.
- Algoritm de sortare in loc, ceea ce înseamnă că nu necesită memorie suplimentară.
Dezavantajele sortării selecției:
- Ineficient pentru seturi mari de date, cu o complexitate de timp în cel mai rău caz de O(n^2).
- Sortarea selecției are o mulțime de comparații, ceea ce o poate face încet pe computerele moderne.
- Algoritm de sortare instabil, ceea ce înseamnă că este posibil să nu mențină ordinea relativă a elementelor egale în matricea de intrare.
În acest articol, vom discuta diferența dintre sortarea prin inserție și sortarea selecție:
Sortare prin inserare este un algoritm simplu de sortare care funcționează similar modului în care sortați cărțile de joc în mâinile tale. Matricea este practic împărțită într-o parte sortată și una nesortată. Valorile din partea nesortată sunt selectate și plasate în poziția corectă în piesa sortată.
Algoritm:
Pentru a sorta o matrice de dimensiunea n în ordine crescătoare:
- Iterați de la arr[1] la arr[n] peste matrice.
- Comparați elementul actual (cheia) cu predecesorul său.
- Dacă elementul cheie este mai mic decât predecesorul său, comparați-l cu elementele de dinainte. Mutați elementele mai mari cu o poziție în sus pentru a face spațiu pentru elementul schimbat.
Mai jos este imaginea pentru a ilustra sortarea inserției:
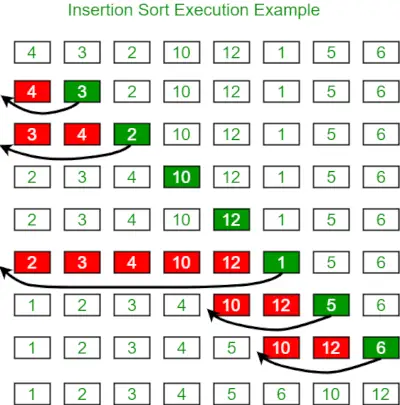
Mai jos este programul pentru același lucru:
C++
// C++ program for the insertion sort> #include> using> namespace> std;> // Function to sort an array using> // insertion sort> void> insertionSort(>int> arr[],>int> n)> {> >int> i, key, j;> >for> (i = 1; i key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> tastă) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = cheie; } } // Funcție de tipărire a unui tablou de dimensiune N void printArray(int arr[], int n) { int i; // Imprimă matricea pentru (i = 0; i cout<< arr[i] << ' '; } cout << endl; } // Driver Code int main() { int arr[] = { 12, 11, 13, 5, 6 }; int N = sizeof(arr) / sizeof(arr[0]); // Function Call insertionSort(arr, N); printArray(arr, N); return 0; }> |
>
>
Java
// Java program for the above approach> import> java.util.*;> class> GFG> {> > // Function to sort an array using> // insertion sort> static> void> insertionSort(>int> arr[],>int> n)> {> >int> i, key, j;> >for> (i =>1>; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> tastă) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = cheie; } } // Funcție de tipărire a unui tablou de dimensiune N static void printArray(int arr[], int n) { int i; // Tipăriți matricea pentru (i = 0; i System.out.print(arr[i] + ' '); } System.out.println(); } // Cod driver public static void main(String[ ] args) { int arr[] = { 12, 11, 13, 5, 6 } int N = arr.length // Apel de inserție(arr, N); Acest cod este contribuit de code_hunt> |
>
>
Python3
# Python 3 program for the insertion sort> # Function to sort an array using> # insertion sort> def> insertionSort(arr, n):> >i>=> 0> >key>=> 0> >j>=> 0> >for> i>in> range>(>1>,n,>1>):> >key>=> arr[i]> >j>=> i>-> 1> ># Move elements of arr[0..i-1],> ># that are greater than key to> ># one position ahead of their> ># current position> >while> (j>>>> and> arr[j]>cheie):> >arr[j>+> 1>]>=> arr[j]> >j>=> j>-> 1> >arr[j>+> 1>]>=> key> # Function to print an array of size N> def> printArray(arr, n):> >i>=> 0> ># Print the array> >for> i>in> range>(n):> >print>(arr[i],end>=> ' '>)> >print>(>'
'>,end>=> '')> # Driver Code> if> __name__>=>=> '__main__'>:> >arr>=> [>12>,>11>,>13>,>5>,>6>]> >N>=> len>(arr)> ># Function Call> >insertionSort(arr, N)> >printArray(arr, N)> > ># This code is contributed by bgangwar59.> |
>
>
C#
// C# program for the above approach> using> System;> class> GFG> {> >// Function to sort an array using> >// insertion sort> >static> void> insertionSort(>int>[] arr,>int> n)> >{> >int> i, key, j;> >for> (i = 1; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> tastă) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = cheie; } } // Funcție de tipărire a unui tablou de dimensiune N static void printArray(int[] arr, int n) { int i; // Tipăriți matricea pentru (i = 0; i { Console.Write(arr[i] + ' '); } Console.WriteLine(); } // Cod driver static public void Main() { int[] arr = new int[] { 12, 11, 13, 5, 6 }; contribuit de Dharanendra L V>>> |
>
>// JavaScript program for the above approach>// Function to sort an array using>// insertion sort>function>insertionSort(arr,n)>{>>let i, key, j;>>for>(i = 1; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> tastă) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = cheie; } } // Funcție de tipărire a unui tablou de dimensiune N function printArray(arr,n) { let i; // Tipăriți matricea pentru (i = 0; i document.write(arr[i] + ' '); } document.write(' '); } // Cod driver let arr=[12, 11 , 13, 5, 6]; let N = arr.length // Apel de inserție (arr, N) // Acest cod este contribuit de avanitrachhadiya2155;>5 6 11 12 13> The sortare de selecție algoritmul sortează o matrice găsind în mod repetat elementul minim (luând în considerare ordinea crescătoare) din partea nesortată și punându-l la început. Algoritmul menține două subbary într-o matrice dată.
- Subbarra este deja sortată.
- Subbaryul rămas nu este sortat.
În fiecare iterație a sortării de selecție, elementul minim (luând în considerare ordinea crescătoare) din subgrupul nesortat este ales și mutat în subbary sortat.
Mai jos este un exemplu pentru a explica pașii de mai sus:
arr[] = 64 25 12 22 11 // Find the minimum element in arr[0...4] // and place it at beginning 11 25 12 22 64 // Find the minimum element in arr[1...4] // and place it at beginning of arr[1...4] 11 12 25 22 64 // Find the minimum element in arr[2...4] // and place it at beginning of arr[2...4] 11 12 22 25 64 // Find the minimum element in arr[3...4] // and place it at beginning of arr[3...4] 11 12 22 25 64>Mai jos este programul pentru același lucru:
C++
// C++ program for implementation of>// selection sort>#include>using>namespace>std;>// Function to swap two number>void>swap(>int>* xp,>int>* yp)>{>>int>temp = *xp;>>*xp = *yp;>>*yp = temp;>}>// Function to implement the selection>// sort>void>selectionSort(>int>arr[],>int>n)>{>>int>i, j, min_idx;>>// One by one move boundary of>>// unsorted subarray>>for>(i = 0; i // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element swap(&arr[min_idx], &arr[i]); } } // Function to print an array void printArray(int arr[], int size) { int i; for (i = 0; i cout << arr[i] << ' '; } cout << endl; } // Driver Code int main() { int arr[] = { 64, 25, 12, 22, 11 }; int n = sizeof(arr) / sizeof(arr[0]); // Function Call selectionSort(arr, n); cout << 'Sorted array: '; // Print the array printArray(arr, n); return 0; }>>>Java
// Java program for implementation of>// selection sort>import>java.util.*;>class>GFG>{>// Function to implement the selection>// sort>static>void>selectionSort(>int>arr[],>int>n)>{>>int>i, j, min_idx;>>// One by one move boundary of>>// unsorted subarray>>for>(i =>0>; i 1; i++) { // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element int temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array static void printArray(int arr[], int size) { int i; for (i = 0; i System.out.print(arr[i]+ ' '); } System.out.println(); } // Driver Code public static void main(String[] args) { int arr[] = { 64, 25, 12, 22, 11 }; int n = arr.length; // Function Call selectionSort(arr, n); System.out.print('Sorted array: '); // Print the array printArray(arr, n); } } // This code is contributed by aashish1995>>>Python3
# Python3 program for implementation of># selection sort># Function to implement the selection># sort>def>selectionSort(arr, n):>># One by one move boundary of>># unsorted subarray>>for>i>in>range>(n>->1>):>># Find the minimum element>># in unsorted array>>min_idx>=>i>>for>j>in>range>(i>+>1>, n):>>if>(arr[j] min_idx = j # Swap the found minimum element # with the first element arr[min_idx], arr[i] = arr[i], arr[min_idx] # Function to print an array def printArray(arr, size): for i in range(size): print(arr[i], end = ' ') print() # Driver Code if __name__ == '__main__': arr = [64, 25, 12, 22, 11] n = len(arr) # Function Call selectionSort(arr, n) print('Sorted array: ') # Print the array printArray(arr, n) # This code is contributed by ukasp>>>C#
algoritmi de căutare
// C# program for implementation of>// selection sort>using>System;>public>class>GFG>{>// Function to implement the selection>// sort>static>void>selectionSort(>int>[]arr,>int>n)>{>>int>i, j, min_idx;>>// One by one move boundary of>>// unsorted subarray>>for>(i = 0; i { // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element int temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array static void printArray(int []arr, int size) { int i; for (i = 0; i Console.Write(arr[i]+ ' '); } Console.WriteLine(); } // Driver Code public static void Main(String[] args) { int []arr = { 64, 25, 12, 22, 11 }; int n = arr.Length; // Function Call selectionSort(arr, n); Console.Write('Sorted array: '); // Print the array printArray(arr, n); } } // This code is contributed by gauravrajput1>>>Javascript
>// Javascript program for implementation of>// selection sort>// Function to implement the selection>// sort>function>selectionSort(arr, n)>{>>let i, j, min_idx;>>>// One by one move boundary of>>// unsorted subarray>>for>(i = 0; i { // Find the minimum element // in unsorted array min_idx = i; for(j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element let temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array function printArray(arr, size) { let i; for(i = 0; i { document.write(arr[i] + ' '); } document.write(' '); } // Driver Code let arr = [ 64, 25, 12, 22, 11 ]; let n = arr.length; // Function Call selectionSort(arr, n); document.write('Sorted array: '); // Print the array printArray(arr, n); // This code is contributed by rag2127>>>Ieșire:Sorted array: 11 12 22 25 64>Diferența tabelară între Sortarea inserției și Sortarea selecției:
Sortare prin inserare Sortare selecție 1. Inserează valoarea în matricea presortată pentru a sorta setul de valori din matrice. Găsește numărul minim/maxim din listă și îl sortează în ordine crescătoare/descrescătoare. 2. Este un algoritm de sortare stabil. Este un algoritm de sortare instabil. 3. Complexitatea timpului în cel mai bun caz este Ω(N) când tabloul este deja în ordine crescătoare. Are Θ(N2) în cel mai rău caz și mediu. În cel mai bun caz, cel mai rău caz și sortarea de selecție medie au complexitatea Θ(N2). 4. Numărul de operații de comparare efectuate în acest algoritm de sortare este mai mic decât schimbarea efectuată. Numărul de operații de comparare efectuate în acest algoritm de sortare este mai mare decât schimbarea efectuată. 5. Este mai eficient decât sortarea Selecție. Este mai puțin eficient decât sortarea Inserție. 6. Aici elementul este cunoscut dinainte și căutăm poziția corectă pentru a le plasa. Locația în care să puneți elementul este cunoscută anterior, căutăm elementul de inserat în acea poziție. 7. Sortarea prin inserare este utilizată atunci când:
- Matricea are un număr mic de elemente
- Au mai rămas doar câteva elemente de sortat
Sortarea de selecție este utilizată când
- O mică listă urmează să fie sortată
- Costul schimbului nu contează
- Verificarea tuturor elementelor este obligatorie
- Costul scrierii în memorie contează ca în memoria flash (numărul de schimburi este O(n) în comparație cu O(n2) de sortare cu bule)
8. Sortarea de inserare este Adaptive, adică eficientă pentru seturile de date care sunt deja sortate substanțial: complexitatea timpului este OK n) când fiecare element din intrare nu este mai mult de k locuri departe de poziția sa sortată Sortarea selecției este un algoritm de sortare prin comparație pe loc
