FORMULA COTANGENTE - TECHCODEVIEW.COM

Trigonometria este o ramură importantă a matematicii care se ocupă cu relația dintre lungimile laturilor și unghiurile unui triunghi dreptunghic. Sinus, cosinus, tangentă, cosecantă, secanta și cotangentă sunt cele șase rapoarte sau funcții trigonometrice. Unde un raport trigonometric este reprezentat ca raportul dintre laturile unui triunghi dreptunghic.

sin θ = latura opusă/ipotenuză
cos θ = latura adiacentă/ipotenuză
tan θ = latura opusă/latura adiacentă
cosec θ = 1/sin θ = ipotenuză/latura opusă
sec θ = 1/cos θ = ipotenuză/latura adiacentă
cot θ = 1/tan θ = latura adiacentă/latura opusă

Formula cotangentă

O funcție cotangentă este o funcție reciprocă a funcției tangente date. Valoarea unui unghi cotangent într-un triunghi dreptunghic este raportul dintre lungimea laturii adiacente unghiului dat și lungimea laturii opuse unghiului dat. Scriem funcția cotangentă ca cot.

Triunghiul ABC

Acum, formula cotangentă pentru unghiul θ este,

cot θ = (partea adiacentă)/(partea opusă)

Funcția cotangentă este pozitivă în primul și al treilea cadran și negativă în al doilea și al patrulea cadran.

cot (2π + θ) = cot θ (1^Sfcadran)
cot (π – θ) = – cot θ (2^ndcadran)
cot (π + θ) = cot θ (3^rdcadran)
cot (2π – θ) = – cot θ (4^thcadran)

Funcția cotangentă este o funcție negativă, deoarece cotangenta unui unghi negativ este negativul unui unghi pozitiv cotangent.

cot (-θ) = – cot θ

În ceea ce privește funcția tangentă, funcția cotangentă se scrie ca:

cot θ = 1/tan θ

(sau)

cot θ = tan (90° – θ) (sau) tan (π/2 – θ)

Funcția cotangentă în termeni de funcții sinus și cosinus poate fi scrisă ca:

cot θ = cos θ/sin θ

Știm că, cot θ = partea adiacentă/partea opusă

Acum împărțiți atât numărătorul, cât și numitorul cu ipotenuza

⇒ cot θ = (partea adiacentă/hipotenuză) / (partea opusă/hipotenuză)

Știm că, sin θ = latura opusă/ipotenuză

cos θ = latura adiacentă/ipotenuză

Prin urmare, cot θ = cos θ/sin θ

Funcția cotangentă în termeni de funcție sinus poate fi scrisă ca,

cot θ = (√1 – sin ² i)/sin i

Știm că, cot θ = cos θ/sin θ

Din identitățile pitagoreice avem;

cos²θ + sin²θ = 1

⇒ cos θ = √1 – sin²i

Prin urmare, cot θ = $frac{sqrt{left(1-sin^{2} heta ight)}}{sin heta}$

Funcția cotangentă în termeni de funcție cosinus poate fi scrisă ca:

cot θ = cos θ/(√1 -cos ² i)

Știm că, cot θ = cos θ/sin θ

Din identitățile pitagoreice avem;
imprimare din java

cos²θ + sin²θ = 1

sin θ = √1 – cos²i

Prin urmare, cot θ = $frac{cos heta}{sqrt{left(1-cos^{2} heta ight)}}$

Funcția cotangentă în termeni de funcții secante și cosecante poate fi scrisă ca,

cot θ = cosec θ/sec θ

Avem, cot θ = cos θ/sin θ

Aceasta poate fi scrisă ca, cot θ = (1/sin θ) / (1/cos θ)

⇒ cot θ = cosec θ/sec θ

Funcția cotangentă în termeni de funcție cosecantă poate fi scrisă ca:

cot θ = √(cosec ² - 1)

Din identitățile pitagoreice, avem,

cosec²θ – pătuț²θ = 1

⇒ patut²θ = 1 – cosec²- 1

Prin urmare, cot θ = √(cosec²- 1)

Funcția cotangentă în termeni de funcție secante poate fi scrisă ca:

cot θ = 1/(√sec ² i – 1)

Din identitățile pitagoreice, avem,

sec²θ – deci²θ = 1

tan θ = √sec²eu – 1

Știm că, cot θ = 1/tan θ

Prin urmare, cot θ = $frac{1}{sqrt{left(1-sec^{2} heta ight)}}$

Tabelul raportului trigonometric

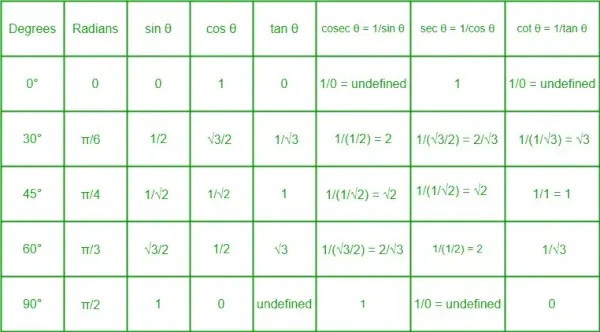
Tabelul cu rapoarte trigonometrice

Legea cotangente sau Legea cotangentelor

Legea cotangentă seamănă cu legea sinusului, dar aici implică jumătate de unghiuri. Legea cotangentelor descrie relația dintre lungimile laturilor triunghiului și cotangentele jumătăților celor trei unghiuri. Să considerăm un triunghi ABC, unde a, b și c sunt lungimile laturilor triunghiului.

Legea cotangentelor prevede că,

$frac{cot(frac{A}{2})}{(s-a)} = frac{cot(frac{B}{2})}{(s-b)} = frac{cot(frac{ C}{2})}{(s-c)} = frac{1}{r}$

Unde s este semiperimetrul triunghiului ABC și r este raza acestuia a cercului înscris al triunghiului.

s = (a + b + c)/2

r = $sqrt{frac{(s-a)(s-b)(s-c)}{s}}$

Exemple de probleme

Problema 1: Aflați valoarea cot θ dacă tan θ = 3/4.

Soluţie:

Date date, tan θ = 3/4

Noi stim aia, cot θ = 1/tan θ

⇒ cot θ = 1/(3/4) = 4/3

Deci, cot θ = 4/3

Problema 2: Aflați valoarea lui cot α, sin α = 1/3 și cos α = 2√2/3.

Soluţie:

Date date, sin α = 1/3 și cos α = 2√2/3

Noi stim aia, cot α = cos α/sin α

⇒ cot α = (2√2/3) / (1/3) = 2√2
livecricket.este

Prin urmare, valoarea cot α = 2√2

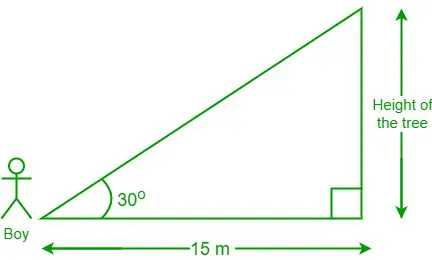
Problema 3: Un băiat care stă la 15 m de un copac se uită la un unghi de 30 de grade la vârful copacului. Care este înălțimea copacului?

Soluţie:

Diagrama din datele date

Date date, distanța dintre băiat și piciorul copacului = 15 m și θ = 30°

Lasă înălțimea copacului să fie „h”

Avem, cot θ = latura adiacentă/latura opusă

⇒ pat 30° = 15/h

⇒ √3 = 15/h [din moment ce, pat 30° = √3]

⇒ h = 15/√3

⇒ h = 5√3 m

Prin urmare, înălțimea copacului = 5√3 m

Problema 4: Aflați valoarea cot x dacă sec x = 6/5.

Soluţie:

Date date, sec x = 6/5

Avem, sec ² x – deci ² x = 1

⇒ (6/5)²- asa de²x = 1

⇒ 36/25 – deci²x = 1

⇒ deci²x = 36/25 – 1

⇒ deci²x = 11/25

⇒ tan x = √(11/25) = √11/5

Noi stim aia, cot x = 1/tan x

⇒ cot x = 1/(√11/5) = 5/√11

Prin urmare, cot x = 5/√11

Problema 5: Aflați valoarea cot θ dacă cosec θ = 25/24.

Soluţie:

Date date, cosec θ = 25/24

Noi stim aia, cot θ = √(cosec ² - 1)

⇒ cot θ = √(25/24)²- 1

⇒ cot θ =√(625 – 576)/576 = √49/576

⇒ cot θ = 7/24
bash dacă altceva

Prin urmare, valoarea cot θ = 7/24

Problema 6: Aflați valoarea lui cot β dacă sin β = 5/13.

Soluţie:

Date date, sin β = 5/13

Noi stim aia, fără ² β + cos ² β = 1

⇒ (5/13)²+ cos²β = 1

⇒ cos²β = 1 – (5/13)²= 1 – 25/169 = 144/169

⇒ cos β = √144/169 = 12/13

cot β = cosβ/sin β

= (12/13) / (5/13)

⇒ pat β = 12/5

Prin urmare, valoarea cot β = 12/5

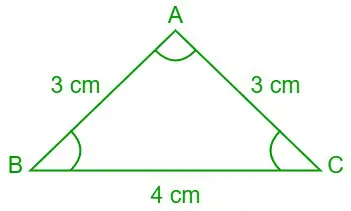
Problema 7: Folosind legea cotangentelor, găsiți valorile lui ∠A, ∠B și ∠C (în grade) dacă lungimile celor trei laturi ale triunghiului ABC sunt a = 4 cm, b= 3 cm și c= 3 cm.

Soluţie:

Dat fiind, a = 4 cm, b = 3 cm și c = 3 cm

Triunghiul ABC

Din legea cotangentelor,

$frac{cot(frac{A}{2})}{(s-a)} = frac{cot(frac{B}{2})}{(s-b)} = frac{cot(frac{ C}{2})}{(s-c)} = frac{1}{r}$

s = (a + b + c)/2

⇒ s = (3 + 4 + 3)/2 = 10/2 = 5

Acum, s – a = 5 – 4 = 1

⇒ s – b = 5 – 3 = 2

⇒ s – c = 5 – 3 = 2

r = $sqrt{frac{(s-a)(s-b)(s-c)}{s}}$

⇒ r = √[(1)(2)(2)/5]

Raza triunghiului r = 2/√5

Din ecuația legii cotangenților,

pat (A/2)/1 = 1/(2/√5)

⇒ pat (A/2) = √5/2 ⇒ A/2 = pat^-1(√5/2)

⇒ (A/2) = 41,8° ⇒ ∠A = 83,6°

cot(B/2)/2 = 1/(2/√5)
dacă-altfel java

⇒ pat (B/2)/2 = √5/2 ⇒ pat (B/2) = √5

⇒ (B/2) = patut^-1(√5) = 24,1° ⇒ ∠B = 48,2°

pat (C/2)/2 = 1/(2/√5)

⇒ pat (C/2) = √5 ⇒ (C/2) = pat^-1(√5)

⇒ (C/2) = 24,1° ⇒ ∠C = 48,2°

Prin urmare, unghiurile triunghiului ABC sunt ∠A = 83,6°, ∠B = 48,2° și ∠C = 48,2°.