Condiție preliminară – Data Mining, măsura de similitudine se referă la distanța cu dimensiuni reprezentând caracteristici ale obiectului de date, într-un set de date. Dacă această distanță este mai mică, va exista un grad ridicat de similitudine, dar când distanța este mare, va exista un grad scăzut de similitudine. Unele dintre măsurile populare de similaritate sunt:
- Distanta euclidiana.
- Distanța Manhattan.
- Asemănarea lui Jaccard.
- Distanța Minkowski.
- Asemănarea cosinusului.
Asemănarea cosinusului este o măsurătoare, utilă pentru a determina cât de asemănătoare sunt obiectele de date, indiferent de dimensiunea lor. Putem măsura asemănarea dintre două propoziții în Python folosind Similitudinea Cosinus. În asemănarea cosinusului, obiectele de date dintr-un set de date sunt tratate ca un vector. Formula pentru a găsi asemănarea cosinusului dintre doi vectori este –
(x, y) = x . y / ||x|| ||y||>
Unde,
- X . y = produsul (punctul) al vectorilor ‘x’ și ‘y’.||x|| și ||și|| = lungimea (magnitudinea) celor doi vectori ‘x’ și ‘y’.||x||
||și|| = produsul regulat al celor doi vectori ‘x’ și ‘y’. Exemplu: Luați în considerare un exemplu pentru a găsi asemănarea dintre doi vectori - 'X' și 'și' , folosind Similitudinea Cosinus. Vectorul „x” are valori, x = { 3, 2, 0, 5 } Vectorul „y” are valori, y = { 1, 0, 0, 0 } Formula de calcul a asemănării cosinusului este: 
(x, y) = x. y / ||x|| ||și||
x . y = 3*1 + 2*0 + 0*0 + 5*0 = 3 ||x|| = √ (3)^2 + (2)^2 + (0)^2 + (5)^2 = 6.16 ||y|| = √ (1)^2 + (0)^2 + (0)^2 + (0)^2 = 1 ∴ (x, y) = 3 / (6.16 * 1) = 0.49>
Diferența dintre cei doi vectori „x” și „y” este dată de -
∴ (x, y) = 1 - (x, y) = 1 - 0.49 = 0.51>
- Asemănarea cosinusului dintre doi vectori este măsurată în „θ”.
- Dacă θ = 0°, vectorii „x” și „y” se suprapun, demonstrând astfel că sunt similari.
- Dacă θ = 90°, vectorii „x” și „y” sunt diferiți.
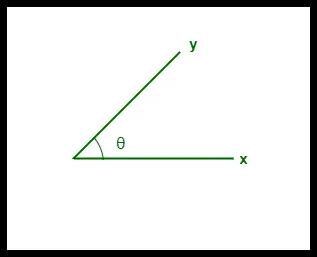
Cosinus Similaritate între doi vectori
Avantaje:
- Asemănarea cosinusului este benefică deoarece, chiar dacă cele două obiecte de date similare sunt departe de distanța euclidiană din cauza dimensiunii, ele ar putea avea totuși un unghi mai mic între ele. Mai mic este unghiul, cu atât mai mare este similaritatea.
- Atunci când este reprezentată pe un spațiu multidimensional, asemănarea cosinusului surprinde orientarea (unghiul) obiectelor de date și nu mărimea.