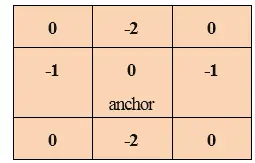
Convoluția este folosită pentru multe lucruri, cum ar fi calcularea derivatelor, detectarea marginilor, aplicarea estompărilor etc. și toate acestea se fac folosind un „nucleu de convoluție”. Un nucleu de convoluție este o matrice foarte mică și în această matrice, fiecare celulă are un număr și, de asemenea, un punct de ancorare.
Punctul de ancorare este folosit pentru a cunoaște poziția nucleului față de imagine. Începe din colțul din stânga sus al imaginii și se mișcă secvenţial pe fiecare pixel. Kernel-ul se suprapune câțiva pixeli în fiecare poziție a imaginii. Fiecare pixel care este suprapus este înmulțit și apoi adăugat. Și suma este setată ca valoare a poziției curente.
Convoluția este procesul în care fiecare element al imaginii este adăugat la vecinii săi locali și apoi este ponderat de nucleu. Este legat de o formă de convoluție matematică.
bandă de bază vs bandă largă
În Convoluție, matricea nu realizează înmulțirea tradițională a matricei, dar este notă cu *.
Să presupunem că există două matrice 3x3, una este nucleu și alta este o bucată de imagine. În convoluție, rândurile și coloanele nucleului sunt răsturnate și apoi sunt înmulțite și apoi se efectuează însumarea. Elementele care sunt prezente în centrul matricei, adică în [2,2] al imaginii, vor fi o combinație ponderată a matricei imaginii, iar ponderile vor fi date de nucleu. În mod similar, toate celelalte elemente ale matricei vor fi ponderate și apoi ponderile vor fi calculate.
Următorul este pseudocodul pentru a descrie procesul de convoluție:
len of string în java
For each image row in input image: For each pixel in image row: Set accumulator to zero For each kernel row in kernel: For each element in kernel row: If element position corresponding* to pixel position then Multiply element value corresponding*to pixelvalue Add result to accumulator Endif Set output image pixel to accumulator
Convoluția poate fi calculată folosind mai multe bucle for. Dar utilizarea buclelor for provoacă multe calcule repetate și, de asemenea, dimensiunea imaginii și a nucleului crește. Folosind tehnica Transformată Fourier discretă, calcularea convoluției se poate face rapid. În această tehnică, întreaga operație de convoluție este convertită într-o simplă înmulțire.
convertiți int în șir de caractere java
În convoluție, problema apare atunci când nucleul este aproape de margine sau colțuri, deoarece nucleul este bidimensional.
Pentru a depăși aceste probleme se pot face următoarele:
- Unele pot fi ignorate
- În apropierea marginilor pot fi creați pixeli suplimentari.
Pixeli suplimentari pot fi creați în următoarele moduri:
- Pixel de margine duplicat.
- Reflectați marginile
- Pixelii pot fi copiați de la celălalt capăt.
